Frequency domain view of the relationship between a signal and a sampling of that signal
A slecture by ECE student Evan Stockrahm
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
Contents
[hide]Outline
- Introduction
- Derivation
- Example
- Conclusion
Introduction
This slecture will discuss the frequency domain view of the relationship between a signal, and a sampling of that signal. Essentially, given a signal x(t), we are going to take a look at the similarities and differences in X(f) and Xs(f). Xs(f) is the Fourier Transform of the sampling, xs(t), of x(t).
Derivation
Given an arbitrary signal x(t), its Fourier Transform is X(f)
The sampling of signal x(t), is the comb of x(t), which is equivalent to multiplying x(t) by the impulse train pT(t).
So, xs(t) = x(t) x pT(t) = combT(x(t))
F(xs(t)) = Xs(f) = (1/T) * rep1/T(X(f))
Analytically, we can see that the frequency domain view of the sampling's amplitude is scaled by a factor of 1/T. The shape of the frequency responses are the same, but it is repeated every 1/T in the sampling's frequency response. In the following example we will see the relationship graphically.
Example
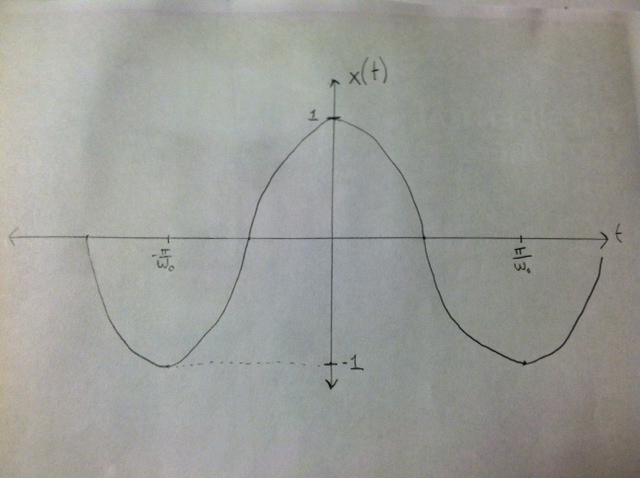
x(t) = cos(wot) (pictured below)
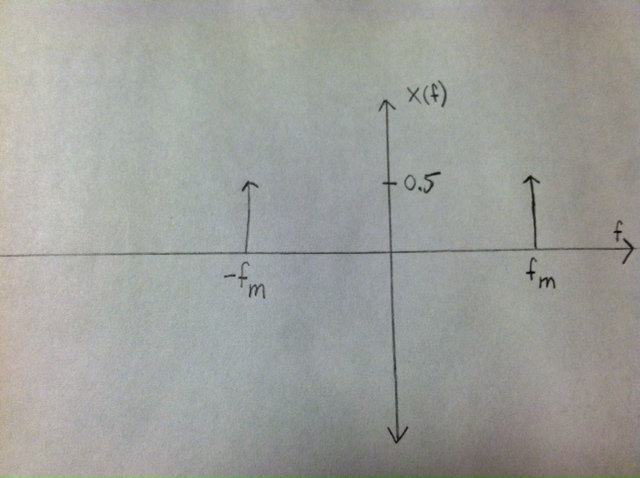
X(f) = pi*(delta(w-wo) + delta(w+wo))
= 1/2*(delta(f - fo) + delta(f + fo)) (pictured below)
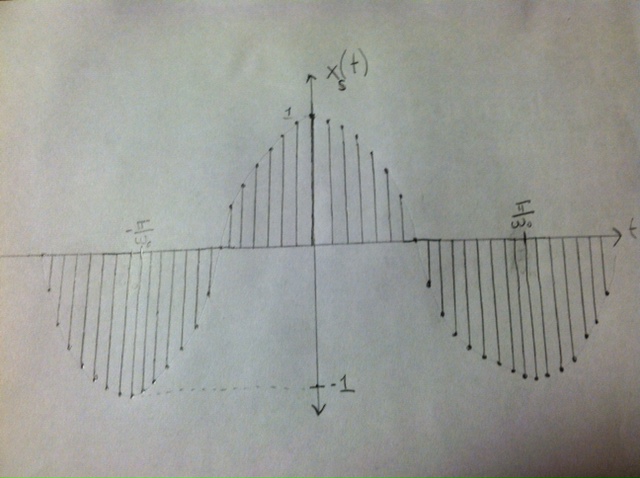
xs(t) = cos(wot) * pT(t)
= combT(cos(wot)) (pictured below)
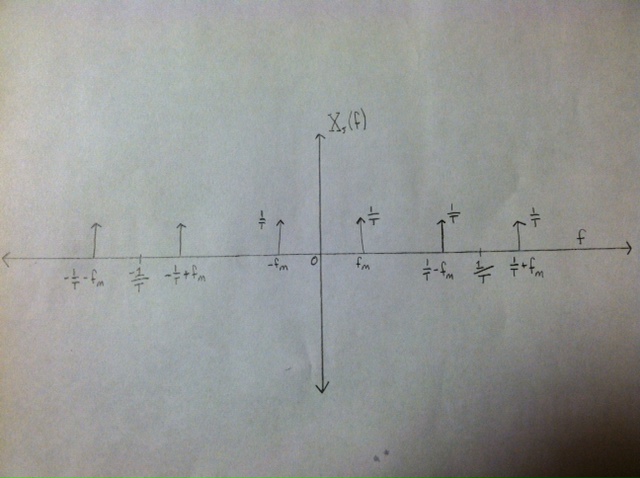
Xs(f) = (1/T)*rep1/T(1/2*(delta(f - fo) + delta(f + fo))) (pictured below)
Conclusion
In conclusion, the frequency domain view of a sampled signal is a scaled and repeated version of the original continuous time signal. The amplitude is scaled by 1/T and the repitition occurs every 1/T.
If you have any questions, comments, etc. please post them right here.