Frequency Domain View of Upsampling
Why Interpolator needs a LPF after Upsampling
A slecture by ECE student Chloe Kauffman
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
Outline
- Background
- Introduction
- Derivation
- Example
- Conclusion
Background
$ {f}_{s} $ = sampling frequency (number of samples/second) Hz
$ {T}_{s} $ = sampling period (number of seconds/sample) seconds
$ {f}_{s} = {\frac{1}{{T}_{s}}} $
Sampling above Nyquist frequency guarantees a bandlimited sampled CT signal's reconstruction. **add source**
Define Nyquist Sampling rate as $ {f}_{Nyquist} = 2{f}_{M} $
$ {f}_{M} $ is max frequency of CT signal
Introduction
Sampling at frequencies much larger than Nyquist requires a filter for reconstruction with a less sharp cutoff. A digital LPF can be used to then obtain the reconstructed signal. *add source*
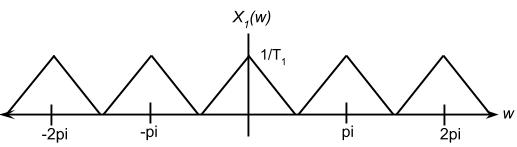
Assume $ {x}_{c}(t) $ is a bandlimited CT signal,
$ {x}_{1}[n] $ is a DT sampled signal of $ {x}_{c}(t) $ with sampling period $ {T}_{1} $
This leads to the question, can you use
$ {x}_{1}[n] = x_{c}(n{T}_{1}) $
to obtain
$ {x}_{u}[n] = {x}_{c}(n{T}_{u}) $, a signal sampled at a HIGHER sampling frequency than $ {x}_{1}[n] $, without having to fully reconstruct $ {x}_{c}(t) $
Derivation
We want $ {f}_{u} > {f}_{Nyquist} $. In this situation, this means $ {f}_{u} > {f}_{1} $.
Therefore, we want $ {T}_{u} < {T}_{1} $. (i.e. $ {x}_{u}[n] $ is sampled at a higher frequency than $ {x}_{1}[n] $)
In other words,
$ {T}_{u} = {\frac{{T}_{1}}{D}} $ for some integer D.
$ {x}_{1}[n] = x_{c}(n{T}_{1}) $
$ {x}_{u}[n] = {x}_{c}(n{T}_{u}) $
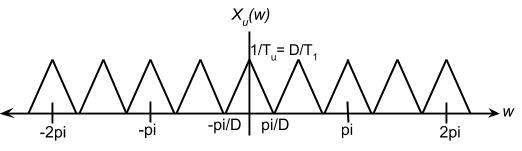
$ {x}_{u}[n] ={x}_{1}[n/D] = {x}_{c}(n{T}_{1}({T}_{u}/{T}_{1})) = {x}_{c}(n{T}_{u}) $if n/D is an integer
$ {x}_{u}[n] = 0 $ else.
In frequency domain:
$ {X}_{u}({\omega}) = {\sum_{n = -{\infty}}^{\infty} {x}_{u}[n]e^{-j{\omega}n}} $
$ {X}_{u}({\omega}) = {\sum_{n = -{\infty}}^{\infty} {x}_{1}[n/D]e^{-j{\omega}n}} $
let n=mD
$ {X}_{u}({\omega}) = {\sum_{m = -{\infty}}^{\infty} {x}_{1}[m]e^{-j{\omega}mD}} $
$ {X}_{u}({\omega}) ={X}_{1}(D{\omega}) $ notice this is a rescaled version of $ {X}_{1} $
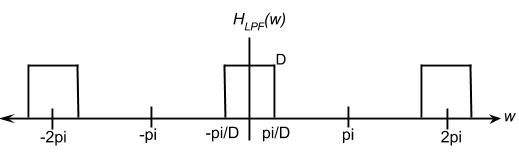
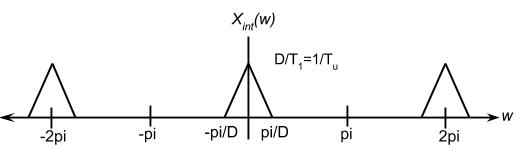
In order to get $ {x}_{int}(n) $, the reconstructed signal, we need to LPF $ {X}_{u}({\omega}) $.
$ {x}_{int}(n) = {x}_{u} * h(n) $
$ h(n) = sinc(n/D) $
Example
Source: Prof. Mireille Boutin