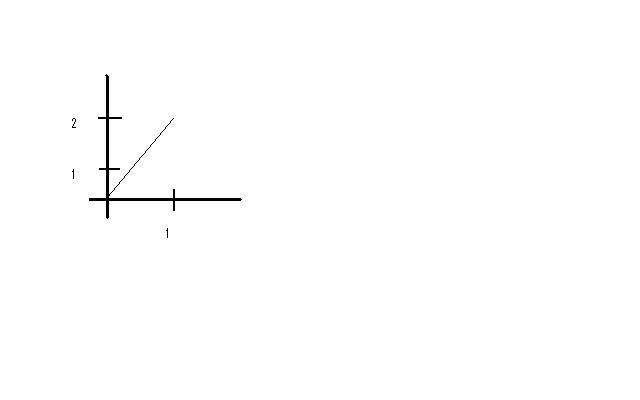Set-Up
- Suppose you have a machine that produces random coins. (Thus, the probability of taking a coin from the machine, tossing it, and getting a 'heads' is a random variable.
- Suppose fQ(q)= 2q for 0<q<1
- If Q = q then P(H|Q=q) = q
- Below graph: fQ(q) vs q
-
Question
- Suppose you take a coin from the Random Coin Machine and toss is. What is the probability of flipping a heads?
Answer
- P(H) $ = \int_{0}^{1}P(H|Q=q) * fQ(q) dq $
$ = \int_{0}^{1}q^2*q dq $
= $ = 2/3 $