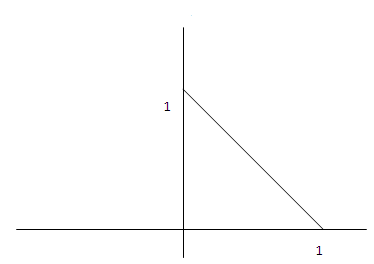
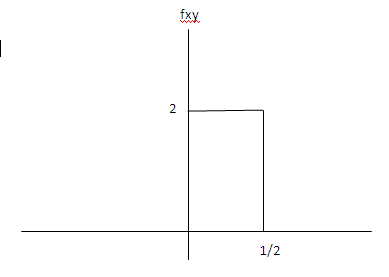
Problem

There are a uniform number of points in the following triangle. Find $ f_{X}(x) $.

Answer

You can only guarantee that there is both a x and y coordinate in the range 0 to 1/2. So the PMF of f_XY(x, y) is as follows:

$ f_{XY}(x, y) = \left\{\begin{array}{ll} 0,& (x, y)\ not\ in\ triangle,\\ 2,& (x, y)\ in\ triangle. \end{array}\right. $

From definition, $ f_{X}(x) = \int_{-\infty}^{\infty}f_{XY}(x, y) dy $
Because if y > (1 - x), there could be a possibility a corresponding x-coordinate is NOT in the triangle, the integral becomes:
$ f_{X}(x) = \int_{0}^{1 - x}2 dy = 2(1 - x) $

Back to ECE302 Fall 2008 Prof. Sanghavi