Neyman-Pearson Lemma and Receiver Operating Characteristic Curve

Partly based on the ECE662 Spring 2014 lecture material of Prof. Mireille Boutin.

INTRODUCTION

The purpose of this slecture is understanding Neyman-Pearson Lemma and Receiver Operating Characteristic (ROC) curve from theory to application. The fundamental theories stem from statistics and these can be used for signal detection and classification. In order to firmly understand these concepts, we will review statistical concept first including False alarm and Miss. After that, we visit Neyman-Pearson Lemma. Lastly, we will discuss ROC curve and its properties. Note that we only consider two classes case in this slecture, but the concept can be extended to multiple classes.

THE GENERAL TWO CLASSES CASE PROBLEM

Before starting our discussion, we have the following setup:

$$ X $$ a measure random variable, random vector, or random process
$x \in \mathcal{X}$ is a realization of $$ X $$
$\theta \in \Theta$ are unknown parameters
$f(x; \theta)$ is pdf of $$ X $$ (a known function)

Two distinct hypotheses on $\theta$ such that $H_0: \theta \in \Theta_0$ versus $H_1: \theta \in \Theta_1$ where $\Theta_0$ , $\Theta_1$ is partition of $\Theta$ into two disjoint regions

\Theta_0 \cup \Theta_1 = \Theta, \qquad \Theta_0 \cap \Theta_1 = \phi

FALSE ALARM RATE AND MISS RATE

From statistical references [1, 2], these two hypotheses make one of two types of error, named Type I Error and Type II Error. If $\theta \in \Theta_0$ but the hypothesis test incorrectly decides to reject $$ H_0 $$ , then the test has made a Type I Error. If, on the other hand, $\theta \in \Theta_1$ but the test decides to accept $$ H_0 $$ a Type II Error has been made. Type I Error is often called false positive error and Type II Error is called false negative error. These two types are depicted in Table 1.

	Decision Accept $$ H_0 $$	Decision Reject $$ H_0 $$
Truth $$ H_0 $$	Correct Decision	Type I Error
Truth $$ H_1 $$	Type II Error	Correct Decision

Table 1: Two types of errors in hypothesis testing.

Different from statistical perspective, engineers focus more on false alarm rate and miss errors rate. False alarm rate is the same as Type I Error such that a given condition has been fulfilled, when it actually has not been fulfilled, that is, erroneously a positive effect has been assumed. Miss rate is such that a given condition has not been fulfilled, when it actually has been fulfilled. In general, to compute miss rate, computing hit rate and subtract hit rate from 1 to get miss rate.

Let's assume a test function $\phi(x)$ such that

\phi(x) = \,

\, \Big\{

1, decide

$ H_1 $

0, decide

$ H_0 $

The test function $\phi(x)$ maps $\mathcal{X}$ to the decision space $\{0, 1\}$ for deciding $$ H_0 $$ and $$ H_1 $$ . The function $\phi(x)$ induces a partition of $\mathcal{X}$ into decision regions. Denote $\mathcal{X}_0 = \{x: \phi(x) = 0 \}$ and $\mathcal{X}_1 = \{x: \phi(x) = 1 \}$ . Then, false alarm and miss probabilities with the function $\phi$ can be expressed as follow:

P_F (\theta) = E_\theta [\phi] = \int_{\mathcal{X}} \phi(x) f(x; \theta) dx, \quad \theta \in \Theta_0

= \int_{\mathcal{X}_1} f(x|\theta) dx, \quad \theta \in \Theta_0

P_M (\theta) = E_\theta [1 - \phi] = \int_\mathcal{X} [1 - \phi(x)] f(x; \theta) dx, \quad \theta \in \Theta_1

= 1 - \int_{\mathcal{X}_1} f(x|\theta) dx, \quad \theta \in \Theta_1.

The probability of correctly deciding $$ H_1 $$ is called hit probability such that

1- P_M (\theta) = P_D(\theta) = E_\theta [\phi], \quad \theta \in \Theta_1.

From the ECE 662 class note [3], Professor Boutin introduced error 1 ( $\epsilon_1$ ) and error 2 ( $\epsilon_2$ ) that are basically same concepts as miss rate and false alarm rate respectively. The only difference is representing the expectation values as fraction as follow:

\epsilon_1 = P_M(\theta)= \frac{\text{Number of test data points labeled as class } \Theta_0 \text{ misclassified as class } \Theta_1}{\text{Number of test data points in class } \Theta_0}

\epsilon_2 = P_F(\theta) = \frac{\text{Number of test data points labeled as class } \Theta_1 \text{ misclassified as class } \Theta_0}{\text{Number of test data points in class } \Theta_1}

NEYMAN-PEARSON LEMMA [4, 5]

The frequentist approach assumes no priors on $$ H_0 $$ or $$ H_1 $$ so one cannot sensibly define an average probability of error of risk to minimize. Thus we adopt the alternative criterion: constrain false alarm and minimize miss probabilities. It turns out that to find an optimum test satisfying such a constraint we will need to extend our previous definition of a test function $\phi$ to allow for randomized decisions such that

\phi(x)= \,

{

1, decide

$ H_1 $

q, flip a coin with Prob{Heads}(

$ H_1 $

) = q

0, decide

$ H_0 $

Note, we have interpretation:

\phi(x) = P(\text{say }H_1 \,|\, \text{ observation }x)

False alarm probability and detection probability are functions of $\theta$

E_\theta [\phi] = \int_{\mathcal{X}} \phi(x) f(x; \theta) dx =

{

P_F(\theta),\,\quad \theta \in \Theta_0

P_D(\theta),\,\quad \theta \in \Theta_1

We define a test $\phi$ is said to be (false alarm) level $\alpha \in [0,1]$ if

\underset{\theta \in \Theta_0} \operatorname{max} P_F(\theta) \leq \alpha

We also define the power function of a test $\phi$ as

\beta(\theta) = P_D (\theta) = 1 - P_M(\theta), \theta \in \Theta_1.

Here, we consider only simple hypotheses case where $\theta \in \{\theta_0, \theta_1\}$

H_0: X \, \sim \, f(x; \theta_0)

H_1: X \, \sim \, f(x; \theta_1)

Then, we will introduce the Neyman-Pearson strategy such that find the most powerful (MP) test $\phi^*$ of level $\alpha$ :

E_{\theta_1} [\phi^*] \geq E_{\theta_1} [\phi]

for any other test satisfying $E_{\theta_0} [\phi] \leq \alpha.$ Note that Neyman-Pearson Lemma is defined as the MP test of level $\alpha \in [0,1]$ is a randomized likelihood ratio test (LRT) of the form

\phi(x)^* = \,

{

1,\, f(x;\,\theta_1) > \eta f(x;\,\theta_0)

q,\, f(x;\,\theta_1) = \eta f(x;\,\theta_0)

0,\, f(x;\,\theta_1) < \eta f(x;\,\theta_0)

where $\eta$ and $$ q $$ are selected to satisfy $E_{\theta_0} [\phi^*] = \alpha.$ Let's denote this LRT as $\Lambda(x)$ . Then, the shorthand LRT notation will be

\Lambda(x) = \frac{f(x;\,\theta_1)}{f(x;\,\theta_0)} \underset{H_0} \overset{H_1} \gtrless \eta.

ROC CURVES FOR THRESHOLD TESTS [5]

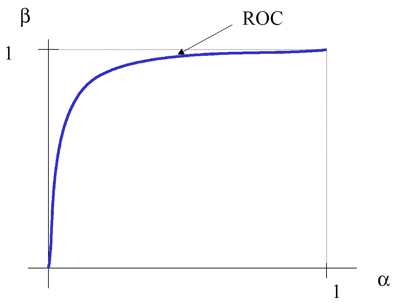
From this section, we will look through the definition of ROC curve and the properties of ROC curve. All threshold tests have $$ P_F $$ and $$ P_D $$ indexed by a parameter $\eta$ . The Receiver Operating Characteristic (ROC) is simply the plot of the parametric curve $\{P_F(\eta, q), P_D(\eta, q)\}_\eta.\,$ Equivalently, ROC is the plot of $\beta = P_D\,$ versus $\alpha = P_F\,$ . A typical ROC curve using these $\alpha$ and $\beta$ is shown in Figure 1.

Figure 1: A typical ROC curve.

This ROC curve has several properties as follow:

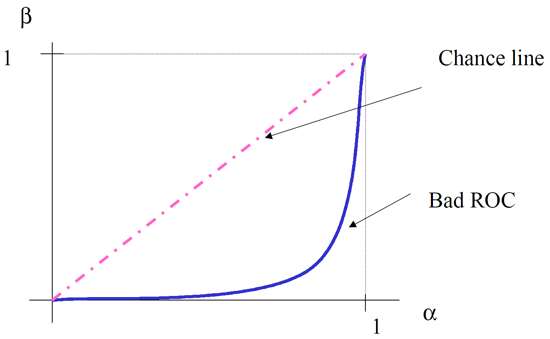
ROC for coin flip detector ( $\phi(x) = q$ independent of data) is a diagonal line with slope = 1. Since this coin flip produces fifty-fifty chances of each output, the chance line is diagonal in ROC curve. Figure 2 is the result for coin flip detector.

\alpha = P_F = E_{\theta_0}[\phi] = q

\beta = P_D = E_{\theta_1}[\phi] = q

Figure 2: ROC curve for coin flip detector.

ROC of any MP test always lies above diagonal. MP test is unbiased test. A test $\phi$ is unbiased if its detection probability $\beta$ is at least as great as its false alarm $\alpha$ : $\beta > \alpha.$ The bad ROC example is shown in Figure 3. As you can see from the figure, good ROC curve should be always above the diagonal.

Figure 3: ROC curve for MP test always lines above diagonal.

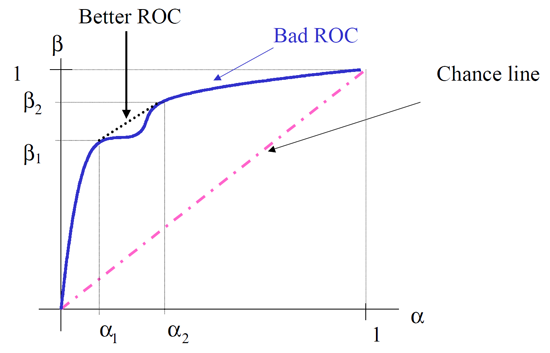
ROC of any MP test is always convex cap (concave). To see concavity, let ( $\alpha_1$ , $\beta_1$ ) be the level and power of a test $\phi_1$ and ( $\alpha_2$ , $\beta_2$ ) be the level and power of a test $\phi_2$ . Define the test

\phi_{12}\,= p \phi_1 + (1-p)\phi_2

This test can be implemented by selecting $\phi_1\,$ and $\phi_2\,$ at random with probability p and 1-p, respectively. The level of this test is

\alpha_{12}\, = E_0[\phi_{12}] = p E_0[\phi_1] + (1-p)E_0[\phi_2] = p\alpha_1 + (1-p)\alpha_2

and its power is similarly

\beta_{12}\, = E_1[\phi_{12}] = p\beta_1 + (1-p)\beta_2.

Thus, as p varies between 0 and 1, $\phi_{12}\,$ has performance $(\alpha_{12},\,\beta_{12})$ which varies on a straight line connecting the points $(\alpha_1,\,\beta_1)$ and $(\alpha_2,\,\beta_2)$ . This property can be easily observed from Figure 4. As depicted from Figure 4, a test with non-convex ROC (thick line) can always be improved by randomization which has effect of connecting two endpoints $(\alpha_1,\,\beta_1)$ and $(\alpha_2,\,\beta_2)$ on ROC by straight line.

Figure 4: ROC curve of any MP test is always convex cap.

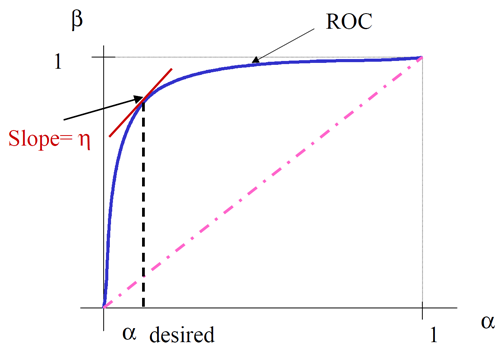
If ROC curve is differentiable, MP-LRT threshold needed for attaining any pair $(\alpha,\,P_D(\alpha))$ on ROC can be found graphically as slope of ROC at the point $\alpha.\,$

\eta = \frac{d}{d\alpha} P_D(\alpha)

The equation above is easily proved as follow:

\frac{d}{d\alpha} P_D(\alpha) = \frac{d P_D}{d P_F} = \frac{\partial P_D}{\partial \eta} \cdot \frac{\partial \eta}{\partial P_F} = \frac{f(\eta; \theta_1)}{f(\eta; \theta_0)} = \eta.

This means we can determine the $\eta$ if an ROC curve and desired $\alpha$ are given. Figure 5 describes this property.

Figure 5: Threshold of MP-LRT can be found by differentiation of ROC curve.

CONCLUSIONS

In this slecture, we reviewed two types of errors $P_F\,$ (False Alarm) and $P_M\,$ (Miss). Since the expression from Statistics and ECE are different, I try to explain two different perspectives. Statisticians mainly focus on Neyman-Pearson Lemma and look for p-value to determine whether reject hypothesis or not. On the other hands, engineers want to know the trends between $P_F\,$ and $P_M\,$ with respect to different threshold. Therefore, ROC curve is very efficient tool for analyzing the problem for engineers. We also briefly reviewed Neyman-Pearson Lemma and the properties of ROC curve.

REFERENCES

[1] G. Casella and R. L. Berger, "Statistical inference (2nd Edition)," Cengage Learning, 2001.
[2] J. K. Ghosh, "STAT528: Introduction to Mathematical Statistics," Fall 2012, Purdue University.
[3] M. Boutin, "ECE662: Statistical Pattern Recognition and Decision Making Process," Spring 2014, Purdue University.
[4] K. Fukunaga, "Introduction to statistical pattern recognition (2nd Edition)," Academic Press, Inc., San Diego, CA, USA, 1990.
[5] A. Hero, "EECS564: Esitmation, Filtering, and Detection," Fall 2010, University of Michigan.

Questions and comments

If you have any questions, comments, etc. please post them on this page.

Back to ECE662, Spring 2014

Neyman-Pearson Lemma and Receiver Operating Characteristic Curve - Rhea

Contents