Limits of Functions

by: Michael Yeh, proud Member of the Math Squad.

 keyword: tutorial, limit, function, sequence 

Introduction

Provided here is a brief introduction to the concept of "limit," which features prominently in calculus. To help motivate the definition, we first consider continuity at a point. Unless otherwise mentioned, all functions here will have domain and range $ \mathbb{R} $, the real numbers. Words such as "all," "every," "each," "some," and "there is/are" are quite important here; read carefully!

Continuity at a point

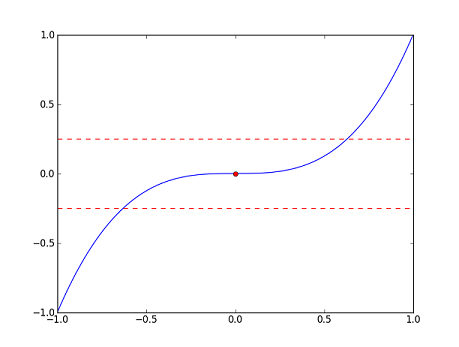
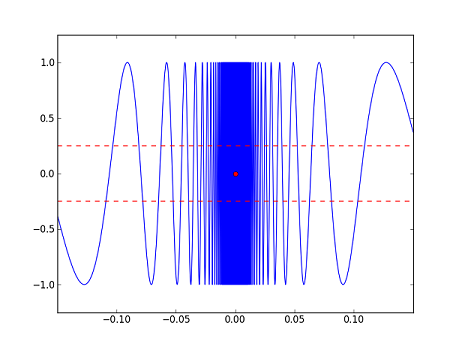
Let's consider the following three functions along with their graphs (in blue). The red dots in each correspond to $ x=0 $, e.g. for $ f_1 $, the red dot is the point $ (0,f_1(0))=(0,0) $. Ignore the red dashed lines for now; we will explain them later.

$ \displaystyle f_1(x)=x^3 $

$ f_2(x)=\begin{cases}-x^2-\frac{1}{2} &\text{if}~x<0\\ x^2+\frac{1}{2} &\text{if}~x\geq 0\end{cases} $

$ f_3(x)=\begin{cases} \sin\left(\frac{1}{x}\right) &\text{if}~x\neq 0\\ 0 &\text{if}~x=0\end{cases} $

We can see from the graphs that $ f_1 $ is "continuous" at $ 0 $, and that $ f_2 $ and $ f_3 $ are "discontinuous" at 0. But, what exactly do we mean? Intuitively, $ f_1 $ seems to be continuous at $ 0 $ because $ f_1(x) $ is close to $ f_1(0) $ whenever $ x $ is close to $ 0 $. On the other hand, $ f_2 $ appears to be discontinuous at $ 0 $ because there are points $ x $ which are close to $ 0 $ but such that $ f_2(x) $ is far away from $ f_2(0) $. The same observation applies to $ f_3 $.

Let's make these observations more precise. First, we will try to estimate $ f_1(0) $ with error at most $ 0.25 $, say. In the graph of $ f_1 $, we have marked off a band of width $ 0.5 $ about $ f_1(0) $. So, any point in the band will provide a good approximation here. As a first try, we might think that if $ x $ is close enough to $ 0 $, then $ f_1(x) $ will be a good estimate of $ f_1(0) $. Indeed, we see from the graph that for any $ x $ in the interval $ (-\sqrt[3]{0.25},\sqrt[3]{0.25}) $, $ f_1(x) $ lies in the band (or if we wish to be more pedantic, we would say that $ (x,f_1(x)) $ lies in the band). So, "close enough to $ 0 $" here means in the interval $ (-\sqrt[3]{0.25},\sqrt[3]{0.25}) $; note that any point which is close enough to $ 0 $ provides a good approximation of $ f_1(0) $.

There is nothing special about our error bound $ 0.25 $. Choose a positive number $ \varepsilon $, and suppose we would like to estimate $ f_1(0) $ with error at most $ \varepsilon $. Then, as above, we can find some interval $ \displaystyle(-\delta,\delta) $ about $ 0 $ (if you like to be concrete, any $ \displaystyle\delta $ such that $ 0<\delta<\sqrt[3]{\varepsilon} $ will do) so that for any $ x $ in $ \displaystyle(-\delta,\delta) $, $ f_1(x) $ will be a good estimate for $ f_1(0) $, i.e. $ f_1(x) $ will be no more than $ \varepsilon $ away from $ f_1(0) $.

Can we do the same for $ f_2 $? That is, if $ x $ is close enough to $ 0 $, then will $ f_2(x) $ be a good estimate of $ f_2(0) $? Well, we see from the graph that $ f_2(0.25) $ provides a good approximation to $ f_2(0) $. But if $ 0.25 $ is close enough to $ 0 $, then certainly $ -0.25 $ should be too; however, the graph shows that $ f_2(-0.25) $ is not a good estimate of $ f_2(0) $. In fact, for any $ x>0 $, $ f_2(-x) $ will never be a good approximation for $ f_2(0) $, even though $ x $ and $ -x $ are the same distance from $ 0 $.

In contrast to $ f_1 $, we see that for any interval $ \displaystyle(-\delta,\delta) $ about $ 0 $, we can find an $ x $ in $ \displaystyle(-\delta,\delta) $ such that $ f_2(x) $ is more than $ 0.25 $ away from $ f_2(0) $.

The same is true for $ f_3 $. Whenever we find an $ x $ such that $ f_3(x) $ lies in the band, we can always find a point $ y $ such that 1) $ y $ is just as close or closer to $ 0 $ and 2) $ f_3(y) $ lies outside the band. So, it is not true that if $ x $ is close enough to $ 0 $, then $ f_3(x) $ will be a good estimate for $ f_3(0) $.

Let's summarize what we have found. For $ f_1 $, we saw that for each $ \varepsilon>0 $, we can find an interval $ \displaystyle(-\delta,\delta) $ about $ 0 $ ($ \displaystyle\delta $ depends on $ \varepsilon $) so that for every $ x $ in $ \displaystyle(-\delta,\delta) $, $ |f_1(x)-f_1(0)|<\varepsilon $. However, $ f_2 $ does not satisfy this property. More specifically, there is an $ \varepsilon>0 $, namely $ \varepsilon=0.25 $, so that for any interval $ \displaystyle(-\delta,\delta) $ about $ 0 $, we can find an $ x $ in $ \displaystyle(-\delta,\delta) $ such that $ |f_2(x)-f_2(0)|\geq\varepsilon $. The same is true of $ f_3 $.

Now we state the formal definition of continuity at a point. Compare this carefully with the previous paragraph.

DEFINITION 1. Let $ f $ be a function from $ \displaystyle A $ to $ \mathbb{R} $, where $ A\subset\mathbb{R} $. Then $ f $ is continuous at a point $ c\in A $ if for every $ \varepsilon>0 $, there is a $ \displaystyle\delta>0 $ such that $ |f(x)-f(c)|<\varepsilon $ for any $ x $ that satisfies $ \displaystyle|x-c|<\delta $. $ f $ is said to be continuous if it is continuous at every point of $ A $.

In our language above, $ \varepsilon $ is the error bound, and $ \displaystyle\delta $ is our measure of "close enough (to $ c $)." Note that continuity is defined only for points in a function's domain. So, the function $ k(x)=1/x $ is technically continuous because $ 0 $ is not in the domain of $ k $. If, however, we defined $ k(0)=0 $, then $ k $ will no longer be continuous.

The Limit of a Function at a Point

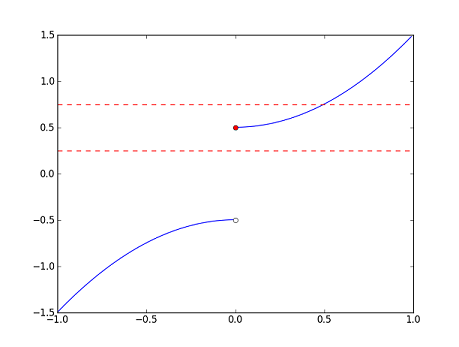
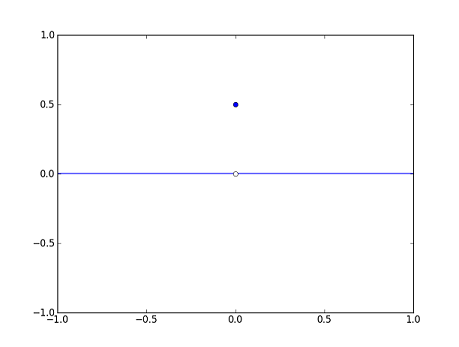
Now, let's consider the two functions $ g_1 $ and $ g_2 $ below. Note that $ g_1 $ is left undefined at $ 0 $.

$ g_1(x)=\begin{cases}-x^2-x &\text{if}~x<0\\ x&\text{if}~x>0\end{cases} $

$ g_2(x)=\begin{cases}0 &\text{if}~x\neq 0\\ \frac{1}{2}&\text{if}~x=0\end{cases} $

Recall the function $ f_1 $ from the previous section. We found that it was continuous at $ 0 $ because $ f_1(x) $ is close to $ f_1(0) $ if $ x $ is close enough to $ 0 $. We can do something similar with $ g_1 $ and $ g_2 $ here. From the graph, we can see that $ g_1(x) $ is close to $ 0 $ whenever $ x $ is close enough, but not equal, to $ 0 $. Similarly, we see that $ g_2(x) $ is close to $ 0 $ whenever $ x $ is close enough, but not equal, to $ 0 $. The "not equal" part is important for both $ g_1 $ and $ g_2 $ because $ g_1 $ is undefined at $ x=0 $ while $ g_2 $ has a discontinuity there. The idea is similar to that of continuity, but we ignore whatever happens at $ x=0 $. We are concerned more with how $ g_1 $ and $ g_2 $ behave around $ 0 $ rather than at $ 0 $. This leads to the following definition.

DEFINITION 2. Let $ f $ be a function defined for all real numbers, with possibly finitely many exceptions, and with range $ \mathbb{R} $. Let $ c $ be any real number. We say that the limit of $ f $ at $ c $ is $ b $, or that the limit of $ f(x) $ as $ x $ approaches $ c $ is $ b $, and write $ \lim_{x\to c}f(x)=b $ if for every $ \varepsilon>0 $, there is a $ \displaystyle\delta>0 $ such that $ |f(x)-b|<\varepsilon $ whenever $ \displaystyle 0<|x-c|<\delta $.

This is the same as the definition for continuity, except we ignore what happens at $ c $. We can see this in two places in the above definition. The first is the use of $ b $ instead of $ f(c) $, and the second is the condition $ \displaystyle 0<|x-c|<\delta $, which says that $ x $ is close enough, but not equal, to $ c $. The restriction on the domain of $ f $ in the above definition is not really necessary; if $ f $ has domain $ A\subset\mathbb{R} $, we can define $ \lim_{x\to c}f(x) $ for any $ c $ which is a "limit point" of $ \displaystyle A $. You can consult Rudin's Principles of Mathematical Analysis, for example, if you're interested. But, in most calculus courses, one usually encounters the situation described in the definition.

If you've ever seen Mean Girls, you know that the limit does not always exist. For example, if $ f_2 $ is the function in the previous section, then $ \lim_{x\to 0}f_2(x) $ does not exist. We will show this rigorously in the exercises, but it is clear from the graph of $ f_2 $.

Having defined what a limit is, we make a few remarks about how continuity and limit are related. As a first observation, we can now restate the definition of continuity at a point more succinctly in terms of limits: $ f $ is continuous at $ c $ if and only if $ \displaystyle\lim_{x\to c}f(x)=f(c) $. Now, let's take a look at the functions $ g_1 $ and $ g_2 $ defined earlier. $ g_1 $ is continuous at every point of its domain; however, it is undefined at $ 0 $. But since $ \lim_{x\to 0}g_1(x) $ exists and equals $ 0 $, we can make $ g_1 $ continuous on the entire real line by defining $ g_1(0)=0 $. We note that even though $ \lim_{x\to 0}g_2(x) $ exists, $ g_2 $ is discontinuous at $ 0 $; this is because $ \lim_{x\to 0}g_2(x)=0\neq \frac{1}{2}=g_2(0) $. This shows that the existence of $ \displaystyle\lim_{x\to c}f(x) $ does not imply continuity at $ c $, even though, as we just mentioned, continuity of $ f $ at $ c $ implies the existence of $ \displaystyle\lim_{x\to c}f(x) $.

Limits at Infinity

Let $ f $ be as in Definition 2. So far, we have only discussed $ \displaystyle\lim_{x\to c}f(x) $ when $ c $ is a real number. It is not difficult to modify Definition 2 for when $ c=\pm\infty $. In Definition 2, we considered $ x $ to be "close enough" when $ x $ is in the interval $ \displaystyle(c-\delta,c+\delta) $ and $ x\neq c $. For $ \infty $, the analogue would be that $ x $ belongs to an interval of the form $ \displaystyle(M,\infty) $, where $ M $ is a real number, and similarly for $ -\infty $. So, we say that the limit of $ f $ at $ \infty $ (respectively, $ -\infty $) is $ b $ and write $ \displaystyle\lim_{x\to\infty}f(x)=b $ (respectively, $ \displaystyle\lim_{x\to-\infty}f(x)=b $) if for every $ \varepsilon>0 $, there is a real number $ M $ so that $ |f(x)-b|<\varepsilon $ whenever $ x>M $ (respectively, $ x<M $).

Exercises

The triangle inequality will be handy for a few of these.

A) Show that any constant function is continuous.

Solution

B) Suppose $ \lim_{x\to c}f(x)=a $ and $ \lim_{x\to c}g(x)=b $. Show that

i)$ \lim_{x\to c}(f+g)(x)=a+b $,

ii)$ \lim_{x\to c}(f-g)(x)=a-b $, and

iii)$ \lim_{x\to c}(fg)(x)=ab $.

Furthermore, if $ b\neq0 $, show that

iv)$ \lim_{x\to c}\left(\frac{f}{g}\right)(x)=\frac{a}{b} $.

As a consequence of A) and B), any polynomial function is continuous.

C) Show that $ \lim_{x\to 0}f_2(x) $ does not exist.

D) Compute the following limits (if they exist):

i)$ \lim_{x\to0}7 $

ii)$ \lim_{x\to2}5x^2-3 $

iii)$ \lim_{x\to+\infty}\frac{2x^2-3x^2-1}{x^3+5} $

iv)$ \lim_{x\to+\infty}\frac{x^3-10x^2+4}{4x^3-2} $

v)$ \lim_{x\to-2}\frac{5x^2-3}{x+2} $

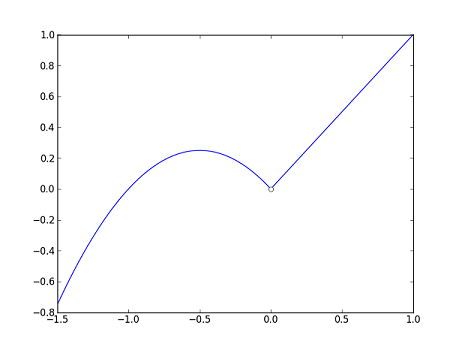
E) (Derivatives) Let $ f $ be a function from $ \mathbb{R} $ to $ \mathbb{R} $ and $ c\in\mathbb{R} $. If $ \lim_{h\to 0}\frac{f(c+h)-f(c)}{h} $ exists, we say that $ f $ is differentiable at $ c $. The above limit is then called the "derivative of $ f $ at $ c $" and is denoted by $ \displaystyle f'(c) $. Intuitively, $ f'(c) $ is the instantaneous rate of change of $ f $ at the point $ c $; it is also the slope of the line tangent to the graph of $ f $ at the point $ (c,f(c)) $.

i) Let $ \displaystyle f(x)=x^2 $. Show that $ f $ is differentiable everywhere, and compute $ \displaystyle f' $.

ii) Let $ \displaystyle g(x)=|x| $. Show that $ g $ is not differentiable at $ 0 $.

Solutions to Exercises

A) Let $ f(x)=k $ be a constant function with value $ k $ and let $ c $ be a real number. Now, let $ \varepsilon>0 $ be given and set $ \displaystyle\delta=1 $. Then for any $ x $ in the interval $ \displaystyle(c-\delta,c+\delta) $, $ |f(x)-f(c)|=|k-k|=0<\varepsilon $.

B) Let $ \varepsilon>0 $ be given. Then we can find a $ \displaystyle\delta_1>0 $ so that $ |f(x)-a|<\varepsilon $ whenever $ \displaystyle0<|x-c|<\delta_1 $, and a $ \displaystyle\delta_2>0 $ so that $ 0<|g(x)-b|<\varepsilon $ whenever $ \displaystyle0<|x-c|<\delta_2 $. Set $ \displaystyle\delta=\min\{\delta_1,\delta_2\} $. Then, for any $ x $ such that $ \displaystyle0<|x-c|<\delta $,

i)

$ |(f+g)(x)-(a+b)|=|(f(x)-a)+(g(x)-b)|\leq|f(x)-a|+|g(x)-b|<\varepsilon+\varepsilon=2\varepsilon $.

Also, it doesn't really matter that we have $ 2\varepsilon $ on the right side instead of $ \varepsilon $ because $ 2\varepsilon $ can be made as small as we like. That is, we can think of $ 2\varepsilon $ as our error bound, instead of $ \varepsilon $.

ii)

$ |(f-g)(x)-(a-b)|=|(f(x)-a)+(b-g(x))|\leq|f(x)-a|+|b-g(x)|<2\varepsilon $.

iii) Note that by the Triangle Inequality, $ |f(x)|-a\leq|f(x)-a|<\varepsilon $ so that $ |f(x)|<|a|+\varepsilon $. Then,

$ \begin{align}|(fg)(x)-ab|&=|f(x)g(x)-f(x)b+f(x)b-ab|\\ &\leq|f(x)g(x)-f(x)b|+|f(x)b-ab|\\ &=|f(x)||g(x)-b|+|f(x)-a||b|\\ &< (|a|+\varepsilon)|g(x)-b|+|f(x)-a||b|\\ &<(|a|+\varepsilon)\varepsilon+\varepsilon|b|\\ &=(|a|+|b|+\varepsilon)\varepsilon\end{align} $

Again, we are fine since $ (|a|+|b|+\varepsilon)\varepsilon $ can be made as small as we like.

iv) By part (iii), it will suffice to show that $ \lim_{x\to c}\left(\frac{1}{g}\right)(x)=\frac{1}{b} $. Let $ \varepsilon>0 $ and set $ \eta=\frac{1}{2}\min\{\varepsilon,|b|\} $. Note that $ \displaystyle\eta>0 $ since $ b\neq 0 $. Therefore, we can find a $ \displaystyle\delta>0 $ so that $ \displaystyle|g(x)-b|<\eta $ whenever $ \displaystyle 0<|x-c|<\delta $. So, if $ \displaystyle 0<|x-c|<\delta $, then $ |g(x)-b|<\varepsilon $ since $ \eta\leq\frac{1}{2}\varepsilon<\varepsilon $. Also, by the triangle inequality we have $ |b|-|g(x)|\leq|b-g(x)|<\eta $. But also, $ \eta\leq\frac{1}{2}b $, so we get $ |g(x)|\geq|b|-\eta\geq|b|-\frac{1}{2}\varepsilon=\frac{1}{2}|b| $. Putting these together, we find that for any $ x $ such that $ \displaystyle 0<|x-c|<\delta $,

$ \bigg|\left(\frac{1}{g}\right)(x)-\frac{1}{b}\bigg|=\frac{|b-g(x)|}{|g(x)||b|}<\frac{\varepsilon}{\left(\frac{1}{2}|b|\right)|b|}=2\frac{\varepsilon}{|b|^2} $.

C) Suppose that the limit did exist, say $ \lim_{x\to 0}f_2(x)=b $. Then setting $ \varepsilon=\frac{1}{4} $, there is a $ \displaystyle\delta>0 $ so that $ |f_2(x)-b|<\varepsilon $ whenever $ \displaystyle 0<|x-0|<\delta $. In particular, $ |f_2(-\frac{1}{2}\delta)-b|<\varepsilon $ and $ |f_2(\frac{1}{2}\delta)-b|<\varepsilon $.

Since $ -\frac{1}{2}\delta<0 $, we have $ f_2(-\frac{1}{2}\delta)=-(-\frac{1}{2}\delta)^2-\frac{1}{2}=(\frac{1}{2}\delta)^2-\frac{1}{2} $, and since $ \frac{1}{2}\delta>0 $, we have $ f_2(\frac{1}{2}\delta)=(\frac{1}{2}\delta)^2+\frac{1}{2}=(\frac{1}{2}\delta)^2-\frac{1}{2} $.

So, $ |f_2(\frac{1}{2}\delta)-f_2(-\frac{1}{2}\delta)|=|2(\frac{1}{2}\delta)^2+1|=2(\frac{1}{2}\delta)^2+1>1 $.

Now, the triangle inequality gives

$ 1<|f_2(\frac{1}{2}\delta)-f_2(-\frac{1}{2}\delta)|=|f_2(\frac{1}{2}\delta)-b+b-f_2(-\frac{1}{2}\delta)|\leq |f_2(\frac{1}{2}\delta)-b|+|b-f_2(-\frac{1}{2}\delta)|<2\varepsilon=\frac{1}{2} $.

But of course, $ 1\nless\frac{1}{2} $, so we obtain a contradiction. This shows that $ \lim_{x\to 0}f_2(x) $ does not exist.

D)

i) $ \displaystyle 7 $

ii) $ \displaystyle 17 $

iii) $ \displaystyle 0 $

iv) $ \frac{1}{4} $

v) does not exist

E)

i) Let $ h $ be a nonzero real number. Then for any $ c $,

$ \frac{(c+h)^2-c^2}{h}=\frac{(c^2+2ch+h^2)-c^2}{h}=\frac{2ch+h^2}{h}=2c+h $.

The limit of the right hand side as $ h $ approaches $ 0 $ exists and equals $ 2c $ using A) and B). Thus, $ f $ is differentiable everywhere, and $ f'(c)=2c $.

ii) Note that for nonzero $ h $,

$ \frac{g(0+h)-g(0)}{h}=\frac{|0+h|-|0|}{h}=\frac{|h|}{h} $.

We notice that for $ h>0 $,

$ \frac{g(0+h)-g(0)}{h}=\frac{|h|}{h}=\frac{h}{h}=1 $

while for $ h<0 $,

$ \frac{g(0+h)-g(0)}{h}=\frac{|h|}{h}=\frac{-h}{h}=-1 $.

Then, as in C), $ \lim_{h\to 0}\frac{g(0+h)-g(0)}{h} $ does not exist. So, $ g $ is not differentiable at $ 0 $.

Questions and comments

If you have any questions, comments, etc. please, please please post them on this page.

Back to Math Squad page