Convolution/Fourier Back Projection Algorithm
A slecture by ECE student Sahil Sanghani
Partly based on the ECE 637 material of Professor Bouman.
Contents
[hide]Introduction
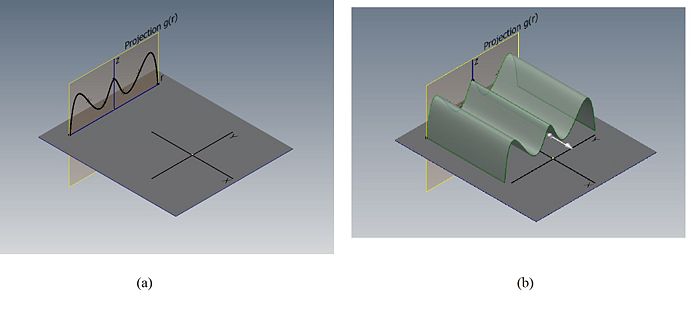
Convolution Back Projection (CBP) offers a reconstruction method that is not computationally expensive. Although the method is based on the Fourier Slice Theorem, there's never a transformation to the frequency domain. Theoretically CBP involves extruding every projection back through the origin and then summing the results. This operation is called back projection. In Figure 1b, the extrusion is demonstrated.
Summary
There are 3 steps to reconstructing an object from its projections using CBP.
1. Measure the projections $ p_{\theta}(r) $. (i.e. using CT)
2. Filter the projections $ g_{\theta}(r) = h(r) * p_{\theta}(r) $
3. Back project filtered projections
$ f(x,y) = \int_0^{\pi}g_{\theta}(x\cos(\theta)+x\sin(\theta))d\theta $
An infinite number of filtered back projections will result in a perfect reconstruction of the original image of the object given it is band limited. Since it is impossible to take that many projections, a good practice is to take at least $ n $ back projections for a $ n $ by $ n $ image.
Derivation
From the Fourier Slice Theorem, we get the following relationships.
$ \begin{align} u &= \rho\cos(\theta) \\ v &= \rho\sin(\theta) \end{align} $
Now let's calculate the Jacobian of the polar coordinate transformation.
$ dudv = \left | \frac{\partial (u,v)}{\partial (\theta,\rho)} \right \vert d\theta d\rho $
$ \begin{align} \left | \frac{\partial (u,v)}{\partial (\theta,\rho)} \right \vert &= det\begin{bmatrix} \frac{\partial u}{\partial \theta} & \frac{\partial u}{\partial \rho} \\ \frac{\partial v}{\partial \theta} & \frac{\partial u}{\partial \rho} \end{bmatrix} \\ &= det\begin{bmatrix} \frac{\partial (\rho\cos(\theta))}{\partial \theta} & \frac{\partial (\rho\cos(\theta))}{\partial \rho} \\ \frac{\partial (\rho\sin(\theta))}{\partial \theta} & \frac{\partial (\rho\sin(\theta))}{\partial \rho} \end{bmatrix} \\ &= det\begin{bmatrix} -\rho\sin(\theta) & \cos(\theta) \\ \rho\cos(\theta) & \sin(\theta) \end{bmatrix} \\ &= |-\rho\sin^{2}(\theta) - \rho\cos^{2}(\theta)| \\ &= |-\rho(\sin^{2}(\theta) + \cos^{2}(\theta))| \\ &= |-\rho| \\ &= |\rho| \\ \end{align} $
$ \Rightarrow dudv = |\rho|d\theta d\rho $
Starting with the formula for the inverse CSFT and using the Fourier Slice theorem, we will end up with
$ \begin{align} f(x,y) &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(u,v)e^{2\pi j(xu+yv)}dudv \\ &= \int_{-\infty}^{\infty}\int_{0}^{\pi}F(\rho\cos(\theta),\rho\sin(\theta))e^{2\pi j(x\rho\cos(\theta) +y\rho\sin(\theta))}|\rho|d\theta d\rho \\ &= \int_0^{\pi}\underbrace{[\int_{-\infty}^{\infty}|\rho|P_{\theta}e^{2\pi j\rho(x\cos(\theta) +y\sin(\theta))}d\rho]}_{g_{\theta}(x\cos(\theta) + y\sin(\theta))}d\theta \end{align} $
Pulling out $ g_{\theta}(t) $,
$ \begin{align} g_{\theta}(t) &= \int_{-\infty}^{\infty}|\rho | P_{\theta}(\rho )e^{2\pi j\rho t} d\rho \\ &= CTFT^{-1}\{|\rho |P_{\theta}(\rho)\} \ \text{, by comparison with the CTFT formula}\\ &= h(t) * p_{\theta}(r) \\ \end{align} $
Projection Filter Analysis
Now let's focus on $ g_{\theta}(r) $.
$ g_{\theta}(r) = h(r) * p_{\theta}(r) \ $
The frequency response of the filter is
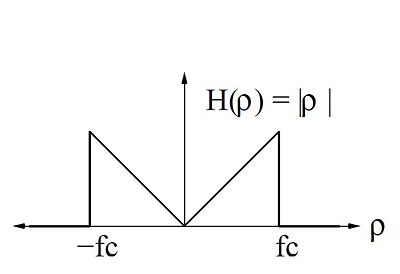
$ H(\rho) = CTFT{(h(r))} = |\rho| \ $
After graphing the frequency response, it is apparent that the filter is a high pass filter.
This filter can be represented by a rect function minus a triangle function, so its equation is
$ \begin{align} H(\rho) &= f_c[rect(f/(2f_c))-\wedge(f/f_c)] \\ h(r) &= f_c^2[2sinc(2f_c t)-sinc^2(tf_c)] \end{align} $
Back Projection Analysis
As mentioned above, the back projection function is
$ f(x,y) = \int_{0}^{\pi} b_{\theta}(x,y)d\theta $
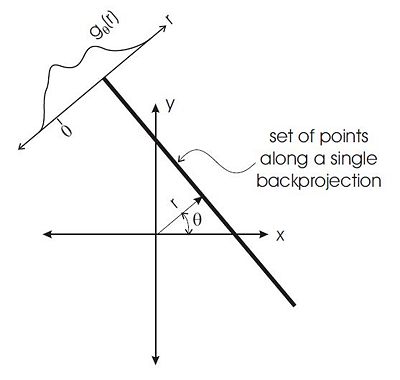
$ b_{\theta}(x,y) = g_{\theta}(x\cos(\theta)+y\sin(\theta)) \ $
For each angle $ \theta $, the back projection value is constant along lines of angle $ \theta $ and takes on the value of $ g_{\theta}(r) $. This is shown in Figure 1 and 3. The complete back projection is formed by integrating(essentially summing) back projections for various $ \theta $. These angles range from $ 0 $ to $ \pi $ because the values start repeating after $ \pi $. An approximation of the CBP is shown below.
$ \begin{align} f(x,y) &= \int_0^{\pi}b_{\theta}(x,y)d\theta \\ &\approx \frac{\pi}{M} \sum_{m=0}^{M-1} b_{\frac{m\pi}{M}}(x,y) \end{align} $
References:
[1] C. A. Bouman. ECE 637. Class Lecture. Digital Image Processing I. Faculty of Electrical Engineering, Purdue University. Spring 2013.
Questions and Comments
Please post your questions and comments on the discussion page.