The Problem: Hillary and Barack have a date, but both are late; each arrives upto 1 hour late. If Hillary comes before Barack, she is angry and cancels the date. If Barack comes before Hillary, he waits for 15 mins, then gets angry and cancels. What is the probability that the date will happen ?
The Solution:
Note that Barack must arrive before Hillary and Hillary must arrive within 15 minutes of Barack for them to meet.
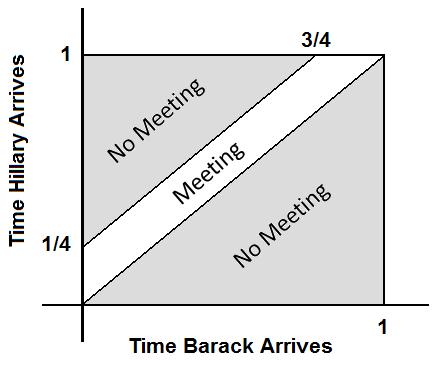
$ \Omega\! $ - the set of all points in $ [0,1]\! $ x $ [0,1]\! $
The probability $ P\! $ of Hillary and Barack meeting is uniform and equal to the area of the unshaded region.
Thus $ P=1-((\frac{1}{2}*1)+(\frac{3}{8}*\frac{3}{4}))=\frac{7}{32} $

