Contents
[hide]Homework 6 Solution, ECE438 Fall 2014, Prof. Boutin
Question 1
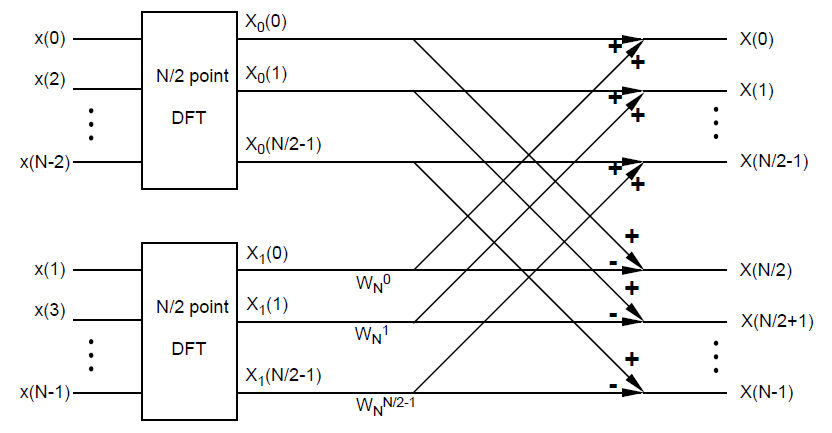
Diagram of "decimation by two" FFT computing N-pt DFT. N=8 in this question.
where $ W_N^k = e^{-j2\pi k/N} $
Recall the definition of DFT:
$ X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N},\ k=0,...,N-1 $.
For each k, we need N times complex multiplications and N-1 times complex additions.
In total, we need $ N^2 = 64 $ times of complex multiplications and $ N^2-N = 56 $ times of complex additions.
Using "decimation by two" FFT algorithm, the DFT is computed in two steps. For the first step, two N/2-pt DFT are computed with $ 2\cdot (\frac{N}{2})^2 $ multiplications and $ 2((\frac{N}{2})^2-\frac{N}{2}) $. For the second step, $ \frac{N}{2} $ multiplications and $ N $ additions are needed.
When $ N=8 $, the total numbers of complex operations are
multiplications: $ 2\cdot (\frac{N}{2})^2 + \frac{N}{2} = 36 $
additions: $ 2((\frac{N}{2})^2-\frac{N}{2}) + N = 32 $
Question 2
Diagram of "radix-2" FFT computing 8-pt DFT.
where $ W_N^k = e^{-j2\pi k/N} $
Recall the definition of DFT:
$ X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N},\ k=0,...,N-1 $
In this question N=8
If we use summation formula to compute DFT, for each k, we need N times complex multiplications and N-1 times complex additions.
In total, we need N*N=64 times of complex multiplications and N*(N-1)=56 times of complex additions.
In decimation-in-time FFT algorithm, we keep on decimating the number of points by 2 until we get 2 points DFT. At most, we can decimate $ v=log_2 N $ times. As a result, we get v levels of DFT. Except for the first level (2-pt FFT), which only needs N times complex additions, for the rest of levels, we need N/2 times of complex multiplications and N times of complex additions.
In total, we need $ \frac{N}{2}(log_2 N -1)=8 $ times of complex multiplications and $ Nlog_2 N=24 $ times of complex additions.
(Note: when $ N $ is large, $ log_2 N -1 \approx log_2 N $. So the number of multiplications becomes $ \frac{N}{2}log_2 N $.)
Question 3
The diagram is identical to the diagram in Question 1 except N=122.
By similar argument presented in Question 1, a direct computation of DFT requires $ N^2 = 14884 $ times of complex multiplications and $ N^2-N = 14762 $ times of complex additions.
Using "decimation by two" FFT algorithm, the total number of multiplications is $ 2\cdot (\frac{N}{2})^2 + \frac{N}{2} = 7503 $ and the total number of additions is $ 2((\frac{N}{2})^2-\frac{N}{2}) + N = 7442 $
Question 4
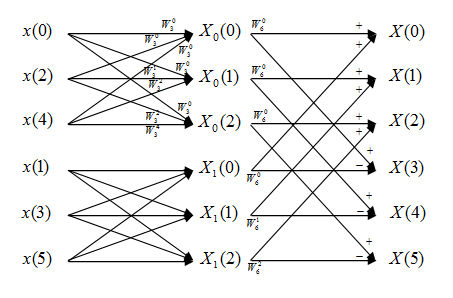
Denote N is the points number of the input signal's DFT. In this question N=6.
1) The normal DFT algorithm: If we use summation formula to compute DFT, according to the analysis of Question 1. We need N*N=36 times of complex multiplications and N*(N-1)=30 times of complex additions.
Flow diagram of FFT:
Analytical Expressions:
$ \begin{align} X_6(k)&=\sum_{n=0}^{5} x(n)e^{-\frac{j2\pi kn}{6}} \\ &\text{Change variable n=2m+l, m=0,1,2; l=0,1 } \\ X_6(k)&=\sum_{l=0}^{1}\sum_{m=0}^{2}x(2m+l)e^{-\frac{j2\pi k(2m+l)}{6}} \\ &=\sum_{l=0}^{1}e^{-\frac{j2\pi kl}{6}}\sum_{m=0}^{2}x(2m+l)e^{-\frac{j2\pi km}{3}} \\ &=\sum_{l=0}^{1}W_6^{kl}X_l(k) \text{ ,k=0,1,...,5 } \end{align} $
Note that $ X_l(k) = X_l(k+3),\ k=0,1,2 $
In this FFT algorithm, the computing of DFT is divided into two levels. First, we compute two 3-point DFT, which are DFT of even and odd points.
In this step we need 4 times of complex multiplications (consider when m=0 and k=0,3, there are no multiplies needed) and 6 times of complex additions for each 3-point DFT. Since we have to do this twice, we need 4*2=8 times of complex multiplications and 6*2=12 times of complex additions.
Second, we compute the final DFT by combing the first level result. According to the analysis of Question 1, we need N/2=3 times of complex multiplications and N=6 times of complex additions.
In total, we need 8+3=11 times of complex multiplications and 12+6=18 times of complex additions.
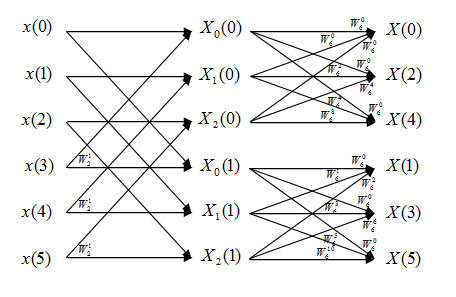
2)
Flow diagram of FFT:
Analytical Expressions:
$ \begin{align} X_6(k)&=\sum_{n=0}^{5} x(n)e^{-\frac{j2\pi kn}{6}} \\ &\text{Change variable n=3m+l, m=0,1; l=0,1,2 } \\ X_6(k)&=\sum_{l=0}^{2}\sum_{m=0}^{1}x(3m+l)e^{-\frac{j2\pi k(3m+l)}{6}} \\ &=\sum_{l=0}^{2}e^{-\frac{j2\pi kl}{6}}\sum_{m=0}^{1}x(3m+l)e^{-\frac{j2\pi km}{2}} \\ &=\sum_{l=0}^{2}W_6^{kl}X_l(k) \text{ ,k=0,1,...,5 } \end{align} $
Note that $ X_l(k) = X_l(k+2) = X_l(k+4),\ k=0,1 $
In this FFT algorithm, the computing of DFT is still divided into two levels. However, we will first compute three 2 points DFT, which are DFT of the first half points and the second half points. According to analysis of Question 1, we need N/2=3 times of complex multiplications and N=6 times of complex additions.
Second, we compute the two 3 points DFT using first level result. we need 4 times of complex multiplications (consider when l=0 and k=0,3 there are no multiplies needed) and 6 times of complex additions for each 3-point DFT. Since we have to do this twice, we need 4*2=8 times of complex multiplications and 6*2=12 times of complex additions.
In total, we need 3+8=11 times of complex multiplications and 6+12=18 times of complex additions.
Note that the output sequences of DFT of 2) is different from 1).
Compare 1) and 2), both methods have the same amount of complex operations.
Question 5
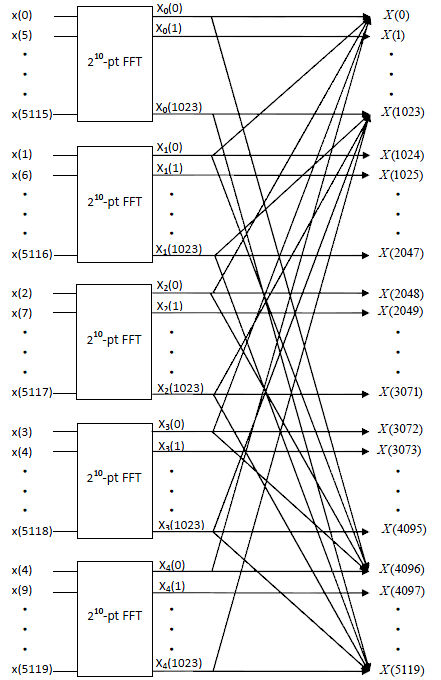
Flow Diagram:
$ 5120=5*1024=5*2^{10} $ So we can split the 5120-point DFT into 5 1024-point DFTs using decimation-in-time and compute the 1024-point DFT using the subroutine of radix 2 FFT.
Analytical expression:
$ \begin{align} X^{(5120)}(k)&=\sum_{n=0}^{5119} x(n)e^{-\frac{j2\pi kn}{5120}} \\ &\text{Change variable n=5m+l, m=0,1,...,1023; l=0,1,...,4 } \\ X^{(5120)}(k)&=\sum_{l=0}^{4}\sum_{m=0}^{1023}x(5m+l)e^{-\frac{j2\pi k(5m+l)}{5120}} \\ &=\sum_{l=0}^{4}e^{-\frac{j2\pi kl}{5120}}\sum_{m=0}^{1023}x(5m+l)e^{-\frac{j2\pi km}{1024}} \\ &=\sum_{l=0}^{4}W_{5120}^{kl}X_l^{(1024)}(k) \text{ ,k=0,1,...,5119 } \end{align} $
Direct computation requires N*N=5120*5120=26214400 times of complex multiplications and N*(N-1)=5120*5119=26209280 times of complex additions.
Using FFT we first perform five 1024-point FFTs, which each require $ \frac{N}{2}log_2 N=512*10=5120 $ complex multiplications and $ Nlog_2 N=1024*10=10240 $ complex additions.
To calculate each of the 5120 final output of the 5120 DFT, we have to perform 5 complex multiplications and 4 complex additions. So we need 5120*5= 25600 times of complex multiplications and 5120*4=20480 times of complex additions.
For the FFT based method we have a total of 5120+25600=30720 complex multiplications and 10240+20480=30720 complex addtions.
By compare the two methods, we see that FFT based method is far more efficient than the direct computation.