Fourier Analysis in Music
by: Maria Bell, proud Member of the Math Squad.
keyword: tutorial, Fourier, Fourier analysis, harmonics
INTRODUCTION This tutorial gives an overview of Fourier analysis and how it can be applied to music to account for differences in musical sounds.
Fourier Analysis
The French mathematician Joseph Fourier discovered that any periodic wave (any wave that consists of a consistent, repeating pattern) can be broken down into simpler waves. In other words, a complicated periodic wave can be written as the sum of a number of simpler waves. Because of their familiarity and usefulness as well-defined functions, mathematicians often use sine and cosine waves as the simple waves, expressing more complicated waves as a sum of sines and cosines with differing amplitudes. Fourier created a method of analysis now known as the Fourier series for determining these simpler waves and their amplitudes from the complicated periodic function.
Musical Application
Sound waves are one type of waves that can be analyzed using Fourier series, allowing for different aspects of music to be analyzed using this method. Musical instruments produce sound as a result of the vibration of a physical object such as a string on a violin, guitar, or piano, or a column of air in a brass or woodwind instrument. This vibration causes a periodic variation in air pressure that is heard as sound. The period T is the length of time before the signal repeats, and the frequency $ f_1 $ equal to 1/T is the fundamental frequency or pitch of the note produced. When this vibration occurs in a musical instrument, not only is the frequency f1 produced, but other frequencies are produced as well. These frequencies are integer multiples of the fundamental frequency f1. Thus, in addition to f1, there are frequencies f2, which equals 2f1, f_3, which equals 3f1, f4, which equals 4f1, and so on. The frequency f1 is called the fundamental, and the frequencies f2, f3, f4, etc. are called the harmonics. We call f2 the second harmonic, f3 the third harmonic and so on. So, for example, the A below middle C has a fundamental frequency of 440 Hertz, a second harmonic of frequency 880 Hertz, a third harmonic of frequency 1320 Hertz, and the k-th harmonic will have a frequency of k*440 Hertz. In principle, there are an infinite number of harmonics, but once the frequency of a harmonic is greater than 20,000 Hertz, the human ear cannot detect it, so these do not contribute to the sound that is heard. When two musical instruments play the same note, the notes have the same pitch for both instruments, but the two instruments sound different; they have different timbres. The reason for this is that the energy in each of the harmonics is different for the two instruments: the amplitudes of the simpler functions making up the complex wave that a person hears as a single note of sound are different. In Fourier analysis, a complicated periodic wave form, x(t), can be written as
$ x(t)=a_0+\sum_{k=1}^\infty\left(a_k\cos(2\pi kt/T)+ b_k\sin(2\pi kt/T)\right), $
where the constants $ a_0 $, $ a_k $, and $ b_k $ are called the Fourier coefficients, and are given by
$ a_0={{1}\over{T}}\int_0^T x(t)\,dt, $
$ a_k={{2}\over{T}}\int_0^T x(t)\cos(2\pi kt/T)\,dt,\quad k=1,2,3,\ldots, $
and
$ b_k={{2}\over{T}}\int_0^T x(t)\sin(2\pi kt/T)\,dt,\quad k=1,2,3,\ldots . $
These Fourier coefficents are equivalent to the amplitudes of the sine and cosine functions corresponding to k-th harmonic (having frequency $ 2\pi k/T $).
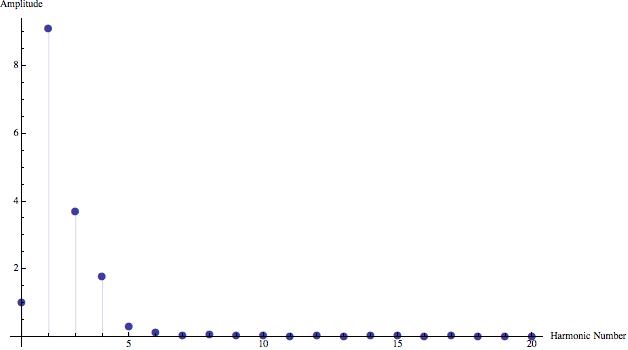
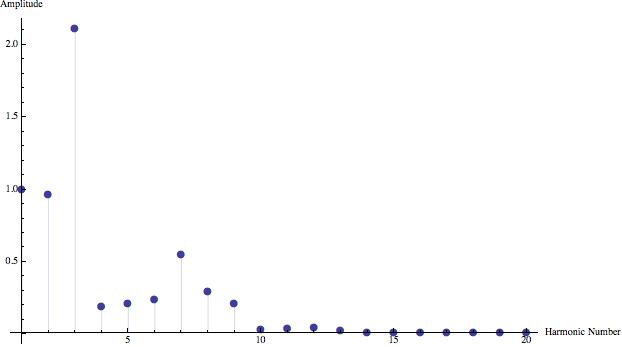
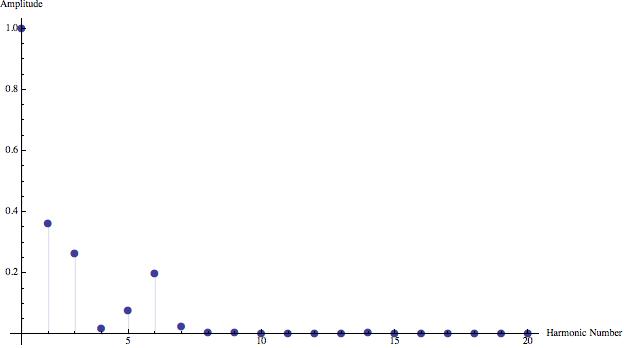
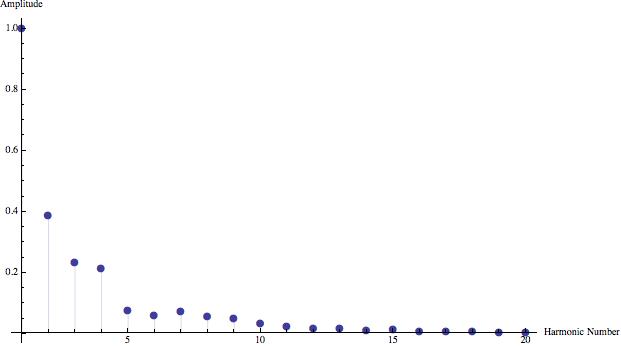
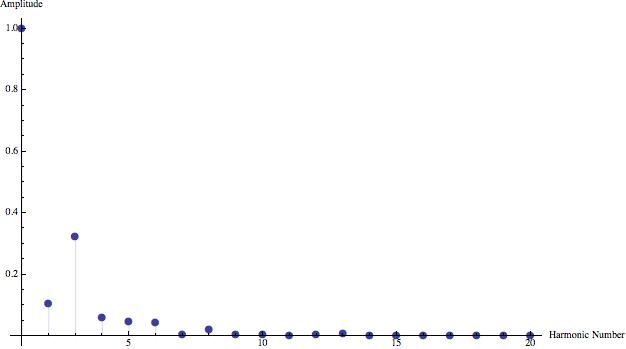
Below are graphs of the Fourier coefficents of the different harmonics for six different musical instruments, all playing the A below middle C (440 Hertz). A single period from the sound wave of each was analyzed using the computer program Mathematica to produce the following data. Here, a_0 was assumed to be zero, and the coefficients were scaled so that the first harmonic for each instrument has a value of one for the sake of comparison.
Listening to these instruments allows for aural distinction of their timbres, Fourier analysis provides mathematical evidence of this difference.
References
- Wolfe, Joe. "What is a Sound Spectrum?" www.phys.unsw.edu.au/~jw/sound.spectrum.html.
- Olson, Harry, F. Music, Physics and Engineering. New York: Dover Publications, 1967.
- Transnational College of LEX. Who Is Fourier? A Mathematical Adventure. Boston: Language Research Foundation, 1998.
The Spring 2013 Math Squad 2013 was supported by an anonymous gift to Project Rhea. If you enjoyed reading these tutorials, please help Rhea "help students learn" with a donation to this project. Your contribution is greatly appreciated.