ECE 438 Fall_2009 Prof. Boutin: graph of the magnitude of the DFT of a windowed filter
Consider the ideal low-pass filter
$ H(\omega)=\left\{ \begin{array}{ll}1, & \text{ when } |\omega|< \omega_c\\ 0, & \text{ when } \omega_c< |\omega|< \pi \end{array}\right., $
which corresponds to the DT signal
$ h[n]=\left\{ \begin{array}{ll} \frac{\omega_c}{\pi}, & \text{ if }n=0,\\ \frac{\sin (\omega_c n)}{\pi n}, & else. \end{array} \right. $
First we shift $ h[n] $ by $ (M-1)/2 $ units.
$ \bar{h}[n]=h[n-\frac{M-1}{2}] $
Then we multiply the result by the window function w[n] where
$ w[n]=\left\{ \begin{array}{ll} 1, & 0 \leq n < M,\\ 0, & else. \end{array} \right. $
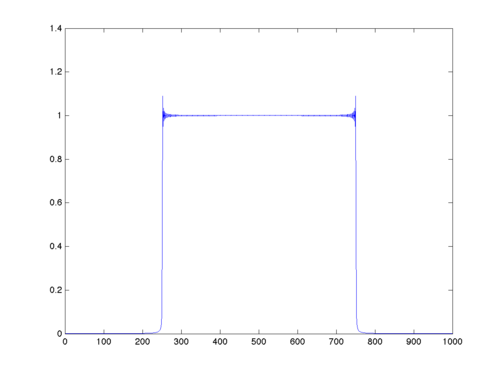
Below is an approximation of the graph of the magniture of
$ H_{FIR}(\omega)=W(\omega)*\bar{H}(\omega) $
for $ M=1,000 $ and $ \omega_c=\frac{\pi}{2} $.
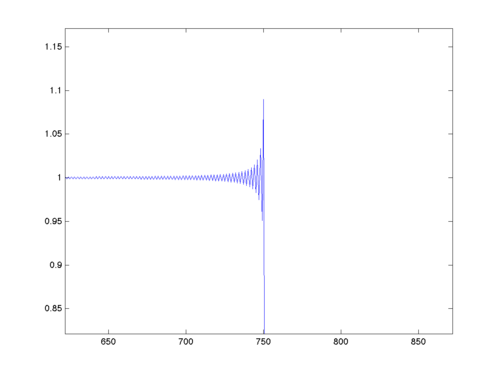
This is a zoom on of of the the little "spiky corners" of the graph of the magniture of $ W(\omega) $
for $ N=1000 $ $ \omega_c=\frac{\pi}{2} $..