ECE662 roc - Rhea

ROC curve and Neyman Pearsom Criterion

A slecture by Hao Lin

Partly based on the ECE662 Spring 2014 lecture material of Prof. Mireille Boutin.

1. Outline of the slecture

Receiver Operating Characteristic (ROC) curve is often used as an important tool to visualize the performance of a binary classifier. The use of ROC curves can be originated from signal detection theory that developed during World War II for radar analysis [2]. What will be covered in the slecture is listed as:

Basics in measuring binary classification
A quick example about ROC in binary classification
Some statistics in ROC curves
Neyman-Pearson Criterion

2. Introduction^[1,2,6]

An ROC curve shows graphically about the trade-off between the true positive rate (TPR) and the false positive rate (FPR). Now assume that we have a two-class prediction problem (binary classification), in which the outcomes are labeled as either class 1 (C1) or class 2 (C2). There are generally four possible outcomes. If the outcome from a prediction is C1 and the actual label is also C1, then it is called a true positive (TP); however if the actual label is C2 then it is said to be a false positive (FP). Conversely, a true negative (TN) has occurred when both the prediction outcome and the actual label are C2, and false negative (FN) is when we predict C2 while the actual label is C1. Usually, the outcomes can be summarized into a contingency table or a Confusion Matrix:

A Confusion Matrix
Actual class \ Predicted class	C1	C2
C1	True Positives (TP)	False Negatives (FN)	P
C2	False Positives (FP)	True Negatives (TN)	N
	P'	N'	All

Each element cell in the matrix gives the frequency of one type of the outcomes. In the signal detection theory, the outcomes have different terms. True positive is also known as a hit, while false positive has another name of a false alarm. True negative and false negative are also known as a correct rejection and a miss respectively. We can further define important measurements oftrue positive rate (TPR, also known as Sensitivity) as TPR = TP/P = TP/(TP+FN), false positive rate (FPR, also known as Fall-out) as FPR = FP/N = FP/(FP+TN).

A ROC curve shows the relationship of TPR over TPR in a x-y plot, which exploits trade-offs between true positive (benefits) and false positive (costs). Any increase in TPR might occur at the cost of an increase in FPR. The area under the ROC curve is a measure of the accuracy of the classifier. The prediction method with the most possible accuracy would yield a point in the upper left corner or coordinate (0,1) of the ROC space, representing 100% sensitivity (no false negatives) and 100% specificity (no false positives). A completely random guess would give a point along a diagonal line from the left bottom to the top right corners (regardless of the positive and negative base rates). An intuitive example of random guessing is a decision by flipping coins (heads or tails). As the size of the sample increases, a random classifier's ROC point migrates towards (0.5,0.5).

3. A quick example about ROC in binary classification^[2]

Here we go over a simple example to plot an ROC curve. We assume that our classifier is able to return a probability of the predicted class for each test record (classifiers based on Bayes Rules can definitely do that). Then we can sort the records by the probability in a decreasing order so that those more likely belong to class C1 come earlier in a list of all records. We can vary a threshold value t, so that records whose probability is greater or equal to t are classified to C1, while other records are considered to belong to C2. With each possible value t in [0, 1], we can compute TPR and FPR, in order to have an ROC curve.

The table below shows a list of records ordered by predicted probability. Column 1 gives the record ID, while Column 2 and 3 list the labels of class and probability values respectively. There are 3 records in class C1 and 3 in C2, i.e.P = 3 and N = 3. Column 4 - 7 gives the records counts with the threshold valuet set to the probability of current record. Accordingly, TPR and FPR can be computed in Column 8 and 9:

Instances sorted by decreasing probability for a given classifier.
ID	Class	Prob.	TP	FP	TN	FN	TPR	FPR
1	C1	0.80	1	0	3	2	0.33	0
2	C2	0.75	1	1	2	2	0.33	0.33
3	C1	0.55	2	1	2	1	0.67	0.33
4	C2	0.50	2	2	1	1	0.67	0.67
5	C1	0.40	3	2	1	0	1.0	0.67
6	C2	0.30	3	3	0	0	1.0	1.0

With some key points obtained by the table above (pairs of TPR and FPR), the ROC curve is the jagged dashed line shown in the figure below:

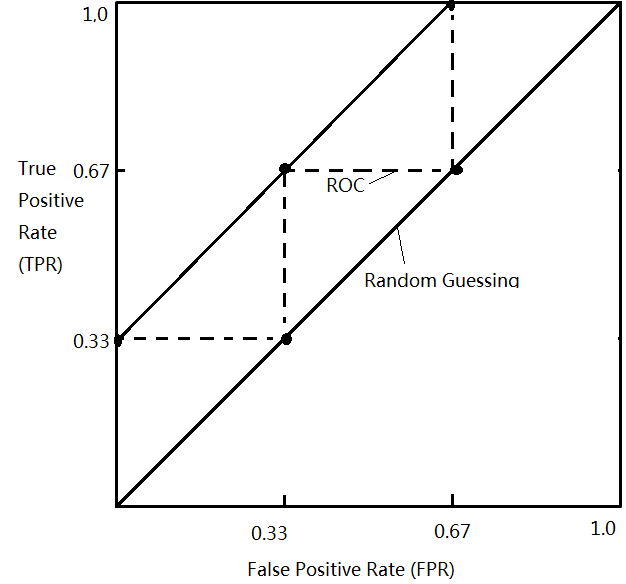
By measuring the area under the curve, we can tell the accuracy of a classifier. A random guess is just the line y = x with an area of 0.5. A perfect model will have a area of 1.0.

4. Some Statistics Under the Hoods^[4,5,7]

In the statistical theory of hypothesis testing, a binary classification problem can also be stated as a binary hypothesis testing (if we assume a simple hypothesis):

$H_0: \theta \in \Theta_0, s.t.\ x\ \sim f_0(x), H_a: \theta \in \Theta_a s.t.\ x\ \sim f_1(x)$

And we use a binary decision rule $\ \phi(x)\$ as a function:

$\ \phi(x) = \begin{cases} 0, decide\ H_0, x \in Region R \\ 1, decide\ H_a, x \in Region R^c \end{cases}$

This means that if x is in the region R, the function $\ \phi(x)=0 \$ and we accept Ho; if x falls out of region R, the function $\ \phi(x)=1 \$ and we accept Ha. In Bayesian Rule, the priors probabilities of each hypothesis are assumed known, and approach to hypothesis testing is represented by the minimum Bayes risk criterion. In some cases, however, it may not be possible to have a prior to a hypothesis, and we need other decision rules like Neyman-Pearson criterion.

Recall that the FPR $P F$ , also known as false alarm rate (probability) or size, is the probability of $\ \phi(x)=1 \$ (x falls out of R and Ha is accepted) but actually Ho is in effect. TPR $P D$ , also known as hit rate or detection rate or power, is the probability of $\ \phi(x)=1 \$ when Ha is indeed in effect. So we have:

\begin{align} P_F &= P_{\theta o}(\phi(x) = 1) = E_{\theta o}[\phi(x)=1] = \int_{R^c} f_0(x) dx \\ P_D &= P_{\theta a}(\phi(x) = 1) = E_{\theta a}[\phi(x)=1] = \int_{R^c} f_1(x) dx \end{align}

An ROC curve is a plot of $P D$ versus $P F$ . Usually multiple $(P D, P F)$ pairs are obtained by adjusting the region of R. AsR grows, both P_D and P_F decrease and approach 0; and as R shrinks, both probabilities increase and approach to 1. Here is an example in the Gaussian case:

Example

Given a simple binary hypothesis test:

$H_0: p(x)\ \sim N(0,1), H_a: p(x)\ \sim N(1,1)$

If we separate the decision region with a threshold $\gamma \in \mathbb{R}$ : if in the region of $x < γ$ , we decide Ho, otherwise Ha is accepted. Then we can compute the false alarm and detection probabilities as:

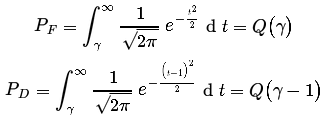
where Q-function is the right-tail probabilities for the Gaussian random variables. So the probability P_D and P_F can be illustrated as the following figure^[5]:

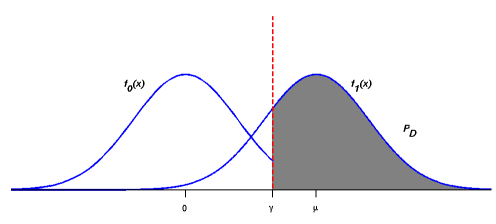
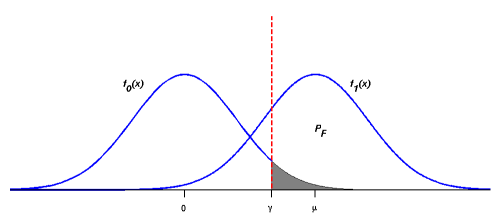
By moving the threshold $γ$ from right to left (decreasingly), we will get an ROC curve of the Gaussian case as following^[5]:

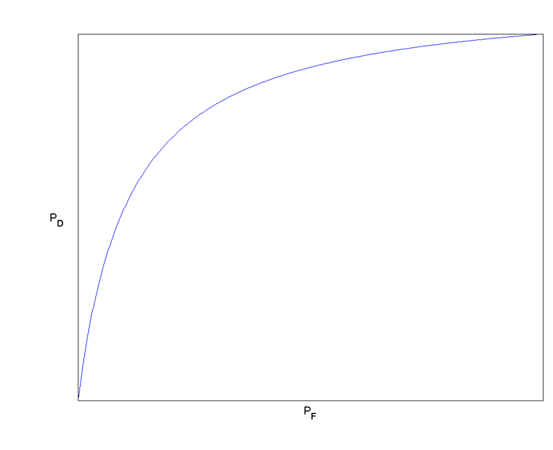
5. Neyman-Pearson Criterion^[7]

Neyman-Pearson criterion aims to have maximum probability of detection (P_D) while not allowing the probability of false alarm (P_F) to exceed a certain value. In the case of simple hypothesis, Neyman-Pearson Lemma proves that it is possible to maximize the power while keep fixed size of the test. If we define the likelihood ratio L(x) as: $L (x) = f θ a (x) / f θ o (x)$ , the Neyman-Pearson lemma says the decision rule is:

$\phi(x) = \begin{cases} 1, L(x) > k \\ \gamma, L(x) = k \\ 0, L(x) < k \end{cases}$

To obey the rule that the test is of give size $α$ (the false alarm rate not exceeding $α$ ), we can compute the value of k and $γ$ by setting the false alarm rate to $α$ :

\begin{align} \alpha = E_{\theta o}[\phi(x)] = P_{\theta o}(L(x) > k) + \gamma P_{\theta o}(L(x) = k) \end{align}

Once we have the value of k and $γ$ , we are guaranteed to have the most powerful test with size of $α$ .

6. Summary

In this slecture, we have covered some basics of ROC curve and Neyman-Pearson Criterion. Some examples are shown to illustrate how an ROC curve is obtained.

Reference

[1] Mireille Boutin, "ECE662: Statistical Pattern Recognition and Decision Making Processes," Purdue University, Spring 2014.
[2] Jiawei Han. 2005. Data Mining: Concepts and Techniques. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA.
[3] Richard O. Duda, Peter E. Hart, and David G. Stork. 2000. Pattern Classification. Wiley-Interscience.
[4] Detection Theory. http://www.ece.iastate.edu/~namrata/EE527_Spring08/l5c_2.pdf.
[5] The Neyman-Pearson Criterion. http://cnx.org/content/m11548/1.2/.
[6] Receiver operating characteristic, Wikipedia. http://en.wikipedia.org/wiki/Receiver_operating_characteristic
[7] Hypothesis Testing. http://people.csail.mit.edu/siracusa/doc/hyptest-faq.pdf

Questions and comments

If you have any questions, comments, etc. please post them on this page.

ECE662 roc - Rhea

Contents

1. Outline of the slecture

2. Introduction^[1,2,6]

3. A quick example about ROC in binary classification^[2]

4. Some Statistics Under the Hoods^[4,5,7]

Example

5. Neyman-Pearson Criterion^[7]

6. Summary

Reference

Questions and comments

Alumni Liaison

ECE662 roc - Rhea

Contents

1. Outline of the slecture

2. Introduction[1,2,6]

3. A quick example about ROC in binary classification[2]

4. Some Statistics Under the Hoods[4,5,7]

Example

5. Neyman-Pearson Criterion[7]

6. Summary

Reference

Questions and comments

Alumni Liaison

2. Introduction^[1,2,6]

3. A quick example about ROC in binary classification^[2]

4. Some Statistics Under the Hoods^[4,5,7]

5. Neyman-Pearson Criterion^[7]