Critically Damped Practice

Question

Find the value for C that will make the zero input response critically damped with roots at -4.

Answer

For a response to be critically damped we know that:
$ b^2 - 4c = 0 $
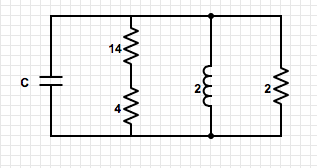
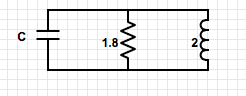
The next step would be to simplify the circuit as shown in the image below. Once simplified it becomes a parallel RLC circuit where we know:
$ b = \frac{1}{RC} $ and $ c = \frac{1}{LC} $

Since the root was given to be -4 we can find b.
$ \frac{-b}{2} = s $ so we get: $ \frac{-b}{2} = -4 $ therefore b = 8.
Once we know b we can use the critically damped equation to solve for C.
$ \begin{align} 8^2 - \frac{4}{2C} = 0\\ 64 = \frac{2}{C}\\ C = \frac{1}{32}\\ \end{align} $

Questions and comments

If you have any questions, comments, etc. please post them below

• Comment 1
  • Answer to Comment 1
• Comment 2
  • Answer to Comment 2

Back to 2015 Spring ECE 201 Peleato

Back to ECE201