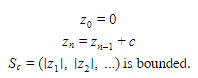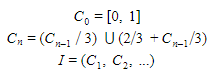PDF Version: File:Proj.pdf
Contents
MA 279, Fall 2018: Fractals and Music
Daniel Atallah, Daksh Jotwani, Zoe Phillips, Noah Talbot
Introduction
“If music is invented to mimic a certain harmony in nature, the mountains are sounds; rivers are lyrics”
- Zhi-Yuan Su and Tzuyin Wu [10]
Humans have always been fascinated by the vast number of patterns scattered throughout our environment. Patterns are a huge part of our daily sights; from branches on a tree, to clouds colliding to form familiar shapes, we seek to find structure in everything we see, hear, and feel around us.
A subset of patterns that we observe has been classified as fractals. The study of these special patterns was mainly developed by a mathematician by the name of Benoit Mandelbrot in the 1980's helped greatly by the use of computers; however, mathematicians have been studying fractals for much longer[1]. Some major players include Weierstrass and Cantor who both contributed to the field in the late 19th century[1]. In March 1918, another mathematician, Felix Hausdorff, introduced fractal dimension, a crucial part of dealing with music as fractals[1]. Their findings all combine to form the rich field of fractal geometry which has applications seemingly far outside mathematics. Fractals are generally depicted visually, since we primarily rely on vision to observe our surroundings. These patterns, however, are also observed in a multitude of natural phenomena, and we seek to explore aural examples of them.
Music is a sequence of temporally structured sounds which are sonically appealing to the human ear. Since music is sequential, aural, and possesses a well-defined structure, exploring the structural patterns of music could lead to observation of some interesting fractals and applications of them. Therefore, we have chosen to explore and document some fascinating musical fractals.
Background
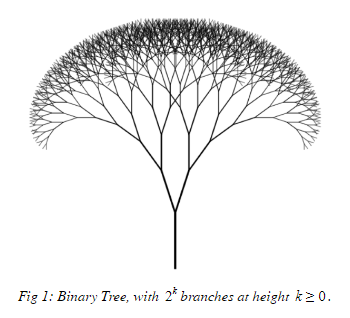
Fractals are infinite self-similar patterns. These patterns are generated by non-terminating sequences, and are usually defined recursively. Fractals are well-observed in nature, and hence are very familiar, as shown by the example below:
The tree above is self-similar, since a new tree can be formed by snapping a branch off the tree. The tree can also be infinitely generated using the following procedure: each branch must split into two new branches. This procedure is also recursive, and is defined concretely as a binary tree in many applications of modern mathematics and computer science.
Fractals can also be generated from abstract mathematical constructs. Two famous examples of these are the Mandelbrot and the Cantor set, which are both briefly explored below:
The Mandelbrot Set is the set of all complex numbers c such that the recursively defined sequence Sc:
In Figure 2, the Mandelbrot set is visually depicted on the complex plane in black, while the other colors depict values of c for with Sc diverges from a predetermined neighborhood n in k iterations, i.e. zk > n. The visual format of the Mandelbrot Set sparked interest amongst many mathematicians, and hence was formally defined as a fractal.
The Cantor Comb, generated by the Cantor Set, is another famous example of a fractal generated from abstract mathematics. Surprisingly, a similar variant of this fractal is observed in various forms of music, one of which we will analyze and discover in greater detail. The Cantor comb can be generated as shown:
The Cantor Comb is a visual depiction of a Cantor set. The process involves generating a set of intervals as defined recursively below:
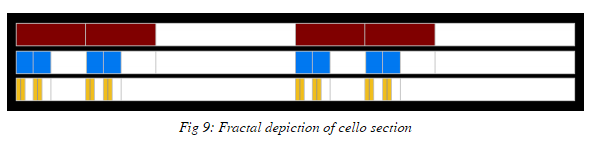
Each interval in I, if plotted sequentially, would generate the Cantor Comb as shown in Figure 3. The fractal above also looks very similar to temporal notation of notes in sheet music. We will explore this set in later parts of our exploration, where we analyze a section of Bach’s Cello Suite 3 and explore similar substructure by removing notes from a simple melody.
We will not require significant knowledge of music theory for this exploration. Whenever a musical term is used, we will provide a brief definition and examples.
Bach’s Cello Suite No. 3
Johann Sebastian Bach’s Cello Suite No. 3 is a classic example of structural symmetry in music. For this example, we will observe the temporal phrasing of the following section shown below:
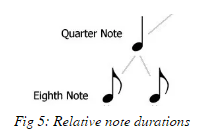
Since we will only be observing temporal phrasing for this example, we will briefly go over some prerequisites to read from the example above using the illustration below:
The figure above portrays the duration each note in the piece above. All we need to know is that the time duration of two eighth notes is equal to one quarter note. For the rest of the discussion, we shall let the time duration of a quarter note be 1 beat. The figure is a subsection of a lot more note duration, but since they do not occur in this piece, we do not discuss them here.
Now, we can simplify the example above into a rhythm line to abstract the rhythmic information of the section:
In the rhythm aspect of the piece, we observe phrasing in the form of three sections: AAB, where the B section is twice as long as the A sections. Starting from the highest form of grouping, we notice that the A lasts 8 beats, while the B section lasts 16 beats.
The second step to forming a fractal from this symmetry is similar to the bisection process of the Cantor Set: we must remove the B section, and recurse on the A sections. Without loss of generality, we describe the recursion on the first A section, since the other split is identical. Therefore, we are now left with the following section of the piece
This section can further be subdivided into AAB sections, with the A section lasting 2 beats, and the B section lasting 4 beats. We repeat the process of discarding the B section, and recursing on the A sections. Finally we get:
Even at the lowest form of the temporal structure, we observe the same AAB structure, with the A sections lasting half a beat, and the B section lasting one beat.
Now that we have observed the structure of this piece, we can generate a fractal from this sub-structure:
This is very similar to the Cantor Comb. While this rhythmic phrasing is subtle, it is definitely audible and aurally satisfying in Bach’s Cello Suite No. 3.
Note Removal Fractal
We will now observe a simple example to generate a three-part section of sheet music which depicts self-similarity:
The above music is an example of self similar music. The top line is the original melody. After removing every other note, you end up with the middle line of music. This is the same melody at half speed. One line further produces the same melody as the first, at quarter speed. The Cantor Set functions similarly. A lot of the music we listen to on a daily basis use techniques like this to captivate the listener. As visual fractals are visually satisfying, fractal music is sonically stimulating.
Music Classification by Fractal Dimension
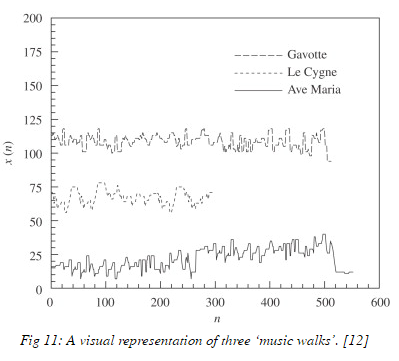
Music and all forms of human creative expression is said to imitate the natural world. Since fractals found throughout nature, it is easy to see why these properties have translated into the world of music. In fact, the fractal properties of music can be a key tool in distinguishing it from noise. A 2007 ‘Physica A’ paper discusses this classification method. This first step in analyzing the fractal nature of any piece of music is to convert the auditory signal into numbers. This paper chose to do this by using the pitch and tone duration of each note to create what they termed a “music walk”. A music walk can then be analysed in the same manner as a standard random walk . The main value of interest is the fractal dimension of the music walk in question. Fractal dimension is discussed further in the appendix. We will see that this is the parameter used in classifying music even further as well. With the music converted into a music walk a method called fractional Brownian Motion (fBm) is used to determine the fractal dimension. Music seems to lie somewhere between being very orderly (Brownian noise) and being completely random (white noise) in fractal dimension [10]. This makes sense as, when you are listening to music, you want enough surprises to keep you interested but not too many that you can’t keep up. However, it is interesting to note that while the too much monotony in a short segment of the music can become boring, on a larger time scale it can give the piece coherence. This can be seen in the fractal dimension of the difference scales[10]. This change in fractal dimension from a short time scale to a long time scale is one of the main features that defines genuine music.
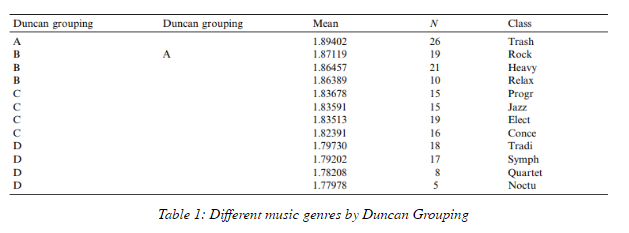
It is clear that music is different from noise; however, we can go a few steps further in classifying music via fractal dimension. Namely, by genre. The method used to do this digitizes the music as a whole to reduce bias introduced by filtering the music or ignoring the interactions between different parts of the music. The fractal dimension in this case in found using a method called the ANAM method[11]. This study analyzed 12 different categories of music and was able to create 8 categories of music that were well defined by the fractal dimension known as Duncan grouping. This categorization had trash music (AKA punk music) in the category with the highest fractal dimension because of its high speed and loud voices, and had Chopin’s Nocturnes in the category with the lowest fractal dimension due to its slow tempo and rhythms [11]. Recalling, the mention of the differences in fractal dimension based on the time scale of the piece being analysed, note that these music genres were analysed on a short time scale as that is how humans listen to music.
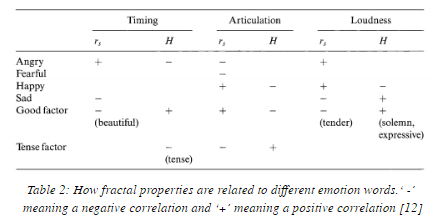
The fractal dimension has even been shown to be related to the emotional expressiveness of music [12]. This is done by looking at the Hurst Exponents H (a parameter directly related to the fractal dimension) and the correlation between rhythmic structure and variability pattern r_s. The emotions studied were anger, fear, happiness, and sadness as well as the goodness of the piece and its tenseness. This classification was done by creating snippets of music with specific values of H and r_s and having participants listen to each piece and determine how well it fit with specific emotions words. The fractal dimension relates to the emotions felt from listening in the timing articulation and loudness of the piece.
Generating Music With Fractals
Since it is clear that music and fractals are related, it is a logical next step to try to create music from fractals. This has been done many times a few of the attempts are detailed below. One paper uses a Java suit to generate music based on known fractals some of which were discussed in the background section[13]. This program allows the user to manipulate the musical parameters to take a simple set of notes into a pieces of art. Another example of fractals being used to create music is Tony Scarpelli using an arduino and a property discussed in [10] of the fractal dimension of music. This property is that music lies about halfway between white noise (random noises, denoted 1/f0) and Brownian noise (highly correlated noise, denoted 1/f2) [14]. This music can be found to download and listen to in this article: https://www.nutsvolts.com/magazine/article/May2016_Fractal_Music_with_Arduino Finally, in his YouTube video [15], Adam Neely uses a property of the relationship between notes to create a composition of Smash Mouth’s “All Star” that is self-similar on two different time scales.
Conclusion
Fractals are amazingly applicable in many realms of study from physics to computer science and possibly most surprisingly music. Music follows the patterns of nature and mathematics it has many fractal properties. Notably, we found examples of music following the Cantor set and displaying self similarity. We have also seen that music can be characterized thoroughly by its fractal dimension. One can tell music from noise, music from other music, and sad music from happy music by just examining the fractal dimension of a piece. Of course it is a little more complicated than that and articles of how any of these processes works for further reading are provided in the references.
References
[1] http://www-groups.dcs.st-and.ac.uk/history/HistTopics/fractals.html
[2] https://fractalfoundation.org/resources/what-are-fractals/
[3] https://giphy.com/gifs/mandelbrot-zooming-Y96cYQ3obJPhe
[4] https://www.bowdoin.edu/~dfrancis/askanerd/mandelbrot/
[5] https://www.youtube.com/watch?v=NGMRB4O922I
[6] http://faculty.bard.edu/belk/math323s11/JuliaSets.pdf
[7] http://www.uwosh.edu/faculty_staff/kuennene/Chaos/ChaosNotes7.pdf
[8] https://www.worldscientific.com/doi/pdf/10.1142/S0218348X0700337X
[9] https://files.eric.ed.gov/fulltext/EJ717806.pdf
[10] https://www.sciencedirect.com/science/article/pii/S0378437107002014#fig1
[11] https://www.sciencedirect.com/science/article/pii/S096007799900137X#FIG3
[12] https://www.tandfonline.com/doi/pdf/10.1080/09298210008565466?needAccess=true
[13] https://www.sciencedirect.com/science/article/pii/S0957417412003338
[14] http://www.nutsvolts.com/magazine/article/May2016_Fractal_Music_with_Arduino
[15] https://www.youtube.com/watch?v=mq0z-sxjNlo&t=379s
[16] https://www.sciencedirect.com/science/article/pii/S0898122101001481
[17] https://arxiv.org/pdf/1611.06190.pdf
Appendix
ANAM - The average normalized autocorrelation method is a method used to find the fractal dimension of curves and surfaces. It was found to define fractal dimension such that classifications of music were most accurate and precise [16]
Complex Number - The sum of a real number and an imaginary number.
Complex Plane - A two-dimensional plane where the horizontal axis is measures real numbers and the vertical axis measures imaginary numbers.
Fractal dimension- This is a measure of how much a curve fills space and the irregularity of a signal. A planar’s fractal dimension is between 1 and 2 meaning it is not quite 1 dimensional nor 2 dimensional. The higher the fractional dimension the more ‘rough’ a curve will be. [17]
Fractional Brownian Motion- a generalization of brownian motion (the motion of a particle in a random walk) with a characteristic property of its Hurst Index H. H is related to fractional dimension by D=2-H. [10]
Random walk - the motion of a ‘walker’ who takes steps in random directions in a given space. [10]
Self Similar- an object that is exactly the same or similar to a smaller part of itself.