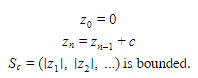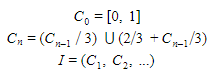PDF Version: File:Proj.pdf
Contents
MA 279, Fall 2018: Fractals and Music
Daksh Jotwani, Daniel Atallah, Noah Talbot, Zoe Phillips
Introduction
“If music is invented to mimic a certain harmony in nature, the mountains are sounds; rivers are lyrics” - Zhi-Yuan Su and Tzuyin Wu
We have always been fascinated by the infinite number of patterns surrounding our environment. Patterns are a huge part of our daily observations; from uniformly distributed branches on a tree, to clouds colliding to form familiar objects, we seek to find structure in everything we see, hear, and feel around us.
A subset of patterns that we observe has been classified as fractals. Fractals are generally depicted visually, since we primarily rely on vision to observe our surroundings. These patterns, however, are also observed in a multitude of natural phenomena, and we seek to explore aural examples of them.
Music is a sequence of temporally structured sounds which are sonically appealing to the human ear. Since music is sequential, aural, and possesses a well-defined structure, we believe that exploring the structural patterns of music could lead to observation of some interesting fractals and applications of them. Therefore, we have chosen to explore and document some fascinating fractals which have been observed in the field of music.
Background
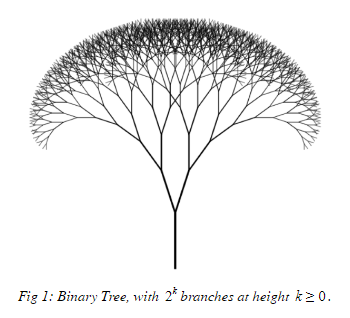
Fractals are infinite self-similar patterns. These patterns are generated by non-terminating sequences, and are usually defined recursively. Fractals are well-observed in nature, and hence are very familiar, as shown by the example below:
The tree above is self-similar, since a new tree can be formed by snapping a branch off the tree. The tree can also be infinitely generated using the following procedure: each branch must split into two new branches. This procedure is also recursive, and is defined concretely as a binary tree in many applications of modern mathematics and computer science.
Fractals can also be generated from abstract mathematical constructs. Two famous examples of these are the Mandelbrot and the Cantor set, which are both briefly explored below:
The Mandelbrot Set is the set of all complex numbers c such that the recursively defined sequence Sc:
In Figure 2, the Mandelbrot set is visually depicted on the complex plane in black, while the other colors depict values of c for with Sc diverges from a predetermined neighborhood n in k iterations, i.e. zk > n. The visual format of the Mandelbrot Set sparked interest amongst many mathematicians, and hence was formally defined as a fractal.
The Cantor Comb, generated by the Cantor Set, is another famous example of a fractal generated from abstract mathematics. Surprisingly, a similar variant of this fractal is observed in various forms of music, one of which we will analyze and discover in greater detail. The Cantor comb can be generated as shown:
The Cantor Comb is a visual depiction of a Cantor set. The process involves generating a set of intervals as defined recursively below:
Each interval in I, if plotted sequentially, would generate the Cantor Comb as shown in Figure 3. The fractal above also looks very similar to temporal notation of notes in sheet music. We will explore this set in later parts of our exploration, where we analyze a section of Bach’s Cello Suite 3 and explore similar substructure by removing notes from a simple melody.
We will not require significant knowledge of music theory for this exploration. Whenever a musical term is used, we will provide a brief definition and examples to provide examples.
Bach’s Cello Suite No. 3
Johann Sebastian Bach’s Cello Suite No. 3 is a classic example of structural symmetry in music. For this example, we will observe the temporal phrasing of the following section shown below:
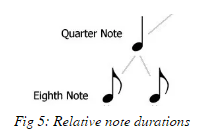
Since we will only be observing temporal phrasing for this example, we will briefly go over some prerequisites to read from the example above using the illustration below:
The figure above portrays the duration each note in the piece above. All we need to know is that the time duration of two eighth notes is equal to one quarter note. For the rest of the discussion, we shall let the time duration of a quarter note be 1 beat. The figure is a subsection of a lot more note durations, but since they do not occur in this piece, we do not discuss them here.
Now, we can simplify the example above into a rhythm line to abstract the rhythmic information of the section:
In the rhythm aspect of the piece, we observe phrasing in the form of three sections: AAB, where the B section is twice as long as the A sections. Starting from the highest form of grouping, we notice that the A lasts 8 beats, while the B section lasts 16 beats.
The second step to forming a fractal from this symmetry is similar to the bisection process of the Cantor Set: we must remove the B section, and recurse on the A sections. Without loss of generality, we describe the recursion on the first A section, since the other split is identical. Therefore, we are now left with the following section of the piece
This section can further be subdivided into AAB sections, with the A section lasting 2 beats, and the B section lasting 4 beats. We repeat the process of discarding the B section, and recursing on the A sections. Finally we get:
Even at the lowest form of the temporal structure, we observe the same AAB structure, with the A sections lasting half a beat, and the B section lasting one beat.
Now that we have observed the structure of this piece, we can generate a fractal from this sub-structure:
[File:Pff9.PNG]]
This is very similar to the Cantor Comb. While this rhythmic phrasing is subtle, it is definitely audible and aurally satisfying in Bach’s Cello Suite No. 3.