U.S. Senate Committee Meetings Scheduling

The United States of America Senate has 16 standing senate committees which meet on a regular basis. These meeting are extremely important as legislation that gets passed in the Senate often originates in these meetings. Each committee is composed of a collection of senate members with the possibility of overlapping members between the committees. Scheduling these meetings in an efficient manner so that we don’t waste time of the committee members is an important problem that needs to be solved. The optimal solution to this problem will be obtained by scheduling multiple meetings within the same time frame, constrained on having no overlapping members between any two concurrent meetings.

Currently, the nation's 16 committees consists of the following sectors:

1. Agriculture, Nutrition, and Forestry
2. Appropriations
3. Armed Services
4. Banking, Housing, and Urban Affairs
5. Budget
6. Commerce, Science, and Transportation
7. Energy and Natural Resources
8. Environment and Public Works
9. Finance
10. Foreign Relations
11. Health, Education, Labor, and Pensions
12. Homeland Security and Governmental Affairs
13. Judiciary
14. Rules and Administration
15. Small Business and Entrepreneurship
16. Veterans' Affairs

Committee Overlaps

Out of the 16 committees there are a total of

Graph coloring is nothing but a simple way of labelling graph components such as vertices, edges, and regions under some constraints. For our problem, we will be considering the vertex coloring variation where no two adjacent vertices are colored with minimum number of colors. This number is called the chromatic number and the graph is called a properly colored graph. The k-coloring of the graph is an assignment of colors to each vertex that meets the above constraints and uses exactly k distinct colors in the coloring. Finding the minimum value of k such that a coloring exist is the problem of interest to us.

The senate committee scheduling problem can be reduced to a graph coloring problem in the following manner. We construct a graph G: Each committee is a vertex. An edge is placed between two vertices if the corresponding committees share a member. We can note that if there exists a k-coloring of this graph, the committee meetings can be scheduled using k time slots. We can simply assign each time slot a color and since each vertex is colored, we get a time slot for each vertex i.e. committee. There can be no conflicts as if any two committees have the same time slot (color), they will not have any common members otherwise there would be an edge between the vertices and by the restriction, the coloring is not valid.

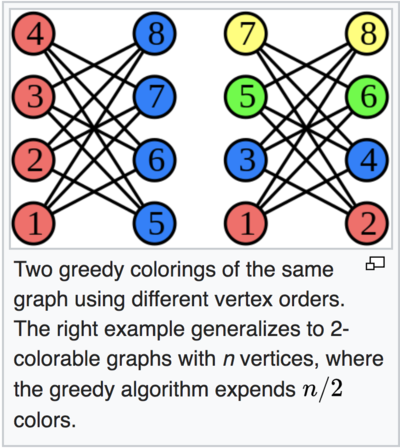
Now, we need to find the minimum k. The importance of finding the minimum is shown below in the figure:

This left image is a 2-coloring of the graph while the right image is a 4-coloring of the same graph. Now, if we interpret the graph in the context of our problem, the 2-coloring uses 2 time slots while the right uses 4. In the 4-coloring, while committees 1 and 2 are in a meeting at a time slot red, the remaining committees are sitting idle which is a waste of senator’s time. Scheduling as many meetings as possible in parallel is the goal. Hence, we want to find the minimum value k can take for out committee graph.

Algorithms

The vertex coloring problem is NP-complete. It can be shown by reducing the 3SAT problem to this problem. This means that there is no known polynomial time algorithm for this problem.

Brute-force search for a k-coloring considers each of the kⁿ assignments of k colors to n vertices and checks for each if it is legal. To compute the chromatic number and the chromatic polynomial, this procedure is used for every k=1, …, n-1, impractical for all but the smallest input graphs. In our case of 16 committees, the worst case is if every member is on every committee, which means we would run our algorithm on all values of k from 1 to 16. This would mean in the worst case looking at  different colorings which is computationally intractable. We can see that for larger values than 16, this value increases very fast.

We can improve upon this naïve method using backtracking. We assign each vertex a color that does not clash with any of its neighboring vertex’s color and repeat the process until we either finish coloring all vertices or have no valid colors left to assign. This avoids looking at coloring where there is more than one point of conflict significantly improving the run time. This method is still exponentially slow in the worst case and even after several heuristics and optimizations, it is still intractable for large graphs. For the purposes of our problems, however, this method is feasible.