| Line 57: | Line 57: | ||
(We note that the term <math> \frac {d^2\psi}{dx^2} </math> is analogous to the curvature of the wavefunction!) | (We note that the term <math> \frac {d^2\psi}{dx^2} </math> is analogous to the curvature of the wavefunction!) | ||
| − | Before we go on to look at solutions to this equation, we must first ask what does this equation mean? Since we have defined our wavefunction across a universe ranging from 0 to <math> V(x)</math>, its curvature basically represents its change in energy as it moves across its defined values. The negative sign is of great implication - as the 'value' of the potential energy of our wavefunction decreases, it is converted into kinetic energy. So even if our wavefunction curves downward measured across its potential energy, it represents a positive increase in its kinetic energy, heeding conservation. | + | Before we go on to look at solutions to this equation, we must first ask what does this equation mean? Since we have defined our wavefunction across a universe ranging from 0 to <math> V(x)</math>, its curvature basically represents its change in energy as it moves across its defined values. The negative sign is of great implication - as the 'value' of the potential energy of our wavefunction decreases, it is converted into kinetic energy. So even if our wavefunction curves downward measured across its potential energy, it represents a positive increase in its kinetic energy, heeding conservation. Consequently, the rate of change of energy - the curvature - is now interpreted to represent the momentum, implying its particle-like nature as well. |
| + | |||
== Solutions == | == Solutions == | ||
| − | Armed with our new equation, we now attempt to determine our allowed wavefunctions. The solutions for this form of Schrodinger's equation are well-documented, and are given in the form : | + | Armed with our new equation, we now attempt to determine our allowed wavefunctions. The solutions for this form of Schrodinger's equation are well-documented, and are given in the form: |
| + | |||
| + | <center><math> \psi(x) = A\sin kx + B\cos kx</math></center> | ||
| + | |||
| + | We can verify this result by simply plugging the solution into the differential equation: | ||
| − | <center><math> | + | <center><math> \frac {d^2\psi}{dx^2} = \frac {d^2}{dx^2} A\sin kx + B\cos kx </math></center> |
Revision as of 15:01, 6 December 2020
Contents
Schrödinger Equation
Varun Chheda
Dr. Walther
Table of Contents
Introduction
The Wavefunction
Particle-in-a-box
Solutions
The Hydrogen Atom
Quantum Tunneling
References and Further Readings
Introduction
First postulated in 1925 by its namesake discoverer, Erwin Schrodinger, the Schrodinger equation is used to describe the wavefunction of particles – that is, an equation that unifies the wave and particle nature of the energy of matter. In its most simple form, it is expressed as a partial differential equation between its energy, representing the wave characteristic, and the Hamiltonian, describing its particle nature. Depending on constraints, the Hamiltonian takes different values - we will be studying in detail the Hamiltonian for a relatively simple equation. The equation became the foundation for the field known today as quantum mechanics. Although expressible in many different forms, in this paper we limit our scope to perhaps the most famous and simple systems, the particle-in-a-box. We will then examine applications of the Schrodinger equation in modeling of the hydrogen atom and quantum tunneling.
The Wavefunction
The wavefunction In order to begin our exploration of the wonder of the Schrodinger equation, we must begin, (as always?), with definition. Central to the Schrodinger equation is the idea of a wavefunction, an equation which, very simply, takes on values based upon the position of the particle in question. Prior to Schrodinger's formulation, physicists had no way of describing both the particle and wave nature of particles in a single equation. Schrodinger's insight was to use the wavefunction as a wave analog to the precise momentum and directions of particles (after all, such terms are meaningless in waves). For our explicit investigation (and my sanity/calculus knowledge) we will limit our calculation to the 1D particle-in-a-box model, but we will discuss radial and angular wavefunctions as applied in hydrogenlike wavefunctions stemming from the Bohr model.
We use $ \psi(x) $ to represent a wavefunction (abbreviated henceforth as $ \psi $) , but what does it mean? Physically, the Born interpretation of the wavefunction states the probability of finding a particle in a given region is proportional to the value of the wavefunction $ \psi $ squared. Indeed, $ \psi^2 $ is given its own definition as a probability density, which we have encountered before - the probability of finding the particle in the region divided by the region's volume.
A final note: Although $ \psi $ can take on negative values, (importantly) $ \psi^2 $ cannot - a result we will require later.
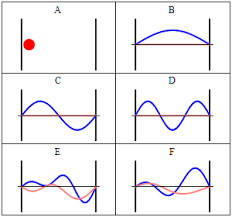
Particle-in-a-box
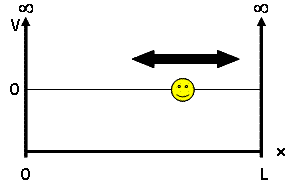
For our discussion, we will be looking at the particle-in-a-box model - a system which defines a particle of mass $ m $ and some potential energy $ V(x) $. This mass is placed into a 'box', a 1D universe of length $ L $ where potential energy is 0 inside the box but infinite outside, confining our particle to the inside of the box:
So what, then, is our equation? We replace our hamiltonian $ \hat H $ with something a little more concrete, and Schrodinger determines this time-independent equation to be:
But as we have just defined, our potential energy $ V(x) $ is 0 everywhere inside the box, leading us to the result
where $ h $ represents Planck's constant.
(We note that the term $ \frac {d^2\psi}{dx^2} $ is analogous to the curvature of the wavefunction!)
Before we go on to look at solutions to this equation, we must first ask what does this equation mean? Since we have defined our wavefunction across a universe ranging from 0 to $ V(x) $, its curvature basically represents its change in energy as it moves across its defined values. The negative sign is of great implication - as the 'value' of the potential energy of our wavefunction decreases, it is converted into kinetic energy. So even if our wavefunction curves downward measured across its potential energy, it represents a positive increase in its kinetic energy, heeding conservation. Consequently, the rate of change of energy - the curvature - is now interpreted to represent the momentum, implying its particle-like nature as well.
Solutions
Armed with our new equation, we now attempt to determine our allowed wavefunctions. The solutions for this form of Schrodinger's equation are well-documented, and are given in the form:
We can verify this result by simply plugging the solution into the differential equation: