Worked Solution using Feynman's Technique
To provide a better understanding of how Feynman's technique, here is another example. Let this function:
The graph of this function looks like this:
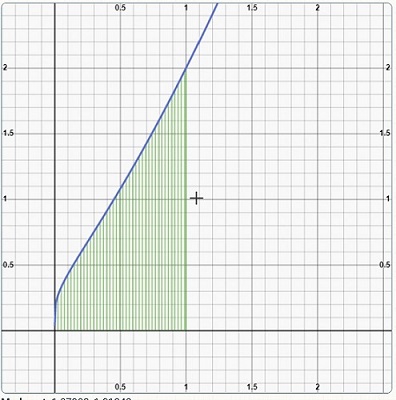
The antiderivative of this function may turn out to be ugly as it involves solving with the exponential and logarithmic integral, but this function can be solved easily if we using differentiation under the integral sign. Therefore, let's define a more basic function:
With this function, our goal is to simplify this function and get a value for F(2) which in turn gives us the answer to the question that was posed. Let's take the derivative of F(b):
According to Feynman's rule, $ \frac{d}{dx}\int_{a}^{b} f(x,y) dx $ = $ \int_{a}^{b} \frac{\partial f(x,y)}{\partial x} dx $

