| Line 79: | Line 79: | ||
'''What is the group SO(3)?''' | '''What is the group SO(3)?''' | ||
| − | + | The special orthogonal group SO(3) is the group of all rotations of R3 about a fixed origin. These rotations about the origin will not only preserve the origin, but also distance. It uses composition (the application of one function to another to produce a third function) as its operation. Every rotation within the SO(3) group, also has an inverse rotation, which would return an object to its original position. Any isometry which preserves the origin is a linear transformation, so if we were to classify the Platonic Solids based on the subgroups of SO(3), we are only worried about groups of rotations with a result about linear groups | |
Revision as of 02:30, 2 December 2013
Classifying Platonic solids via subgroups of SO(3)
by Lance Von Ah
What are Platonic Solids?
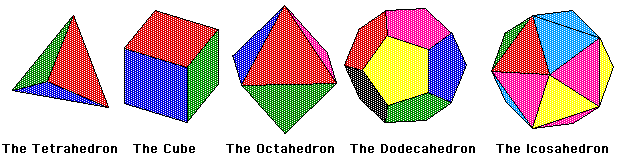
The Platonic Solids are the only regular convex polyhedra. This means they are an object bounded by planes in R3, in which all its faces are congruent regular polygons and the same number of faces meet at each vertex. There are only five of these objects; the tetrahedron, the hexahedron (or cube), the octahedron, the dodecahedron, and the icosahedron. These objects were very intriguing to the ancient Greeks who found their symmetry fascinating. They became known as the Platonic solids from the Greek philosopher Plato who theorized the four classical elements (Air, Fire, Water, and Earth) were made from these solids.
Why only 5 Platonic solids?
Euclid argues in Book XIII of Elements that there can only be five platonic solids and no others possible. He does so by giving a geometric argument which is outlined below:
1. Each vertex of the solid must be made up by the edge of three or more faces.
2. At each vertex of the solid, the sum of the angles formed by the faces at a vertex need to be less than 360 degrees.
3. Since there needs to be three or more faces at each vertex and each face’s angle is the same, then the angles of all the faces of the solid must be less than 120 degrees.
4. Possible faces of the solid:
•Regular Triangle: each angle of a regular triangle is 60 degrees, so a Platonic Solid may have a vertex where 3 triangles (tetrahedron), 4 triangles (octahedron), or 5 triangles (icosahedron) meet. 6 triangles meeting at a vertex result in an angle of 360 degrees which could not create a 3D object.
•Regular Square: each angle of a regular square is 90 degrees, so a Platonic Solid may have a vertex where 3 squares meet (hexahedron). Like 6 triangles, 4 squares meeting a vertex result in an angle of 360 degrees.
•Regular Pentagon: each angle of a regular pentagon is 108 degrees, so a Platonic Solid may have a vertex where 3 pentagons meets (dodecahedron).
•Regular Polygons with more than 5 sides: each angle of a regular polygon with more than 5 sides has an angle greater than or equal to 120 degrees. Thus, no Platonic Solid could be created from them.
Numberphile does a great visual demonstration of this proof: [1]
| Platonic Solid | Number of faces (F) | Number of edges (E) | Number of vertices (V) | Edges per face |
|---|---|---|---|---|
| Tetrahedron | 4 | 6 | 4 | 3 |
| Hexahedron(Cube) | 6 | 12 | 8 | 4 |
| Octahedron | 8 | 12 | 6 | 3 |
| Dodecahedron | 12 | 30 | 20 | 5 |
| Icosahedron | 20 | 30 | 12 | 3 |
What is the group SO(3)?
The special orthogonal group SO(3) is the group of all rotations of R3 about a fixed origin. These rotations about the origin will not only preserve the origin, but also distance. It uses composition (the application of one function to another to produce a third function) as its operation. Every rotation within the SO(3) group, also has an inverse rotation, which would return an object to its original position. Any isometry which preserves the origin is a linear transformation, so if we were to classify the Platonic Solids based on the subgroups of SO(3), we are only worried about groups of rotations with a result about linear groups
--Lvonah 12:41, 1 December 2013 (UTC)