| Line 78: | Line 78: | ||
'''Definitons:''' | '''Definitons:''' | ||
| − | *For every <math>a, b \in G</math> there exists <math> c \in [<a,b>,<a,b>]</math> such that <nowiki>a^p b^p = (ab)^p c^p</nowiki> | + | *For every <math>a, b \in G</math> there exists <math> c \in [<a,b>,<a,b>]</math> such that <nowiki>a^p b^p = (ab)^p c^p</nowiki> |
*For every <math>a, b \in G</math> there exist <math>c_i \in [<a,b>,<a,b>]</math> such that <math>a^p b^p = (ab)^p c^p _1 c^p _2 . . . c^p _i</math> | *For every <math>a, b \in G</math> there exist <math>c_i \in [<a,b>,<a,b>]</math> such that <math>a^p b^p = (ab)^p c^p _1 c^p _2 . . . c^p _i</math> | ||
| − | *For evert <math>a, b \in G</math> and every positive integer < | + | *For evert <math>a, b \in G</math> and every positive integer <span class="texhtml">''n''</span> there exist elements <math>c_i \in [<a,b>,<a,b>]</math> such that <math>a^q b^q = (ab)^q c^q _1 c^q _2 . . . c^q _i</math> where <span class="texhtml">''q'' = ''p''<sup>''n''</sup></span> |
<br> <br> | <br> <br> | ||
== Sylow's Theorems == | == Sylow's Theorems == | ||
| − | |||
'''Notation:''' | '''Notation:''' | ||
| Line 104: | Line 103: | ||
All content from this section and proofs of these Theorems can be found [http://math.berkeley.edu/~sikimeti/SylowNotes.pdf here] | All content from this section and proofs of these Theorems can be found [http://math.berkeley.edu/~sikimeti/SylowNotes.pdf here] | ||
| + | <br> '''Application of Sylow theorems''' | ||
| − | |||
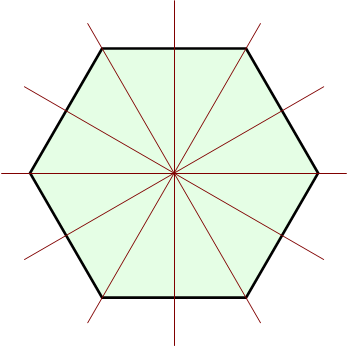
*In D<sub>6</sub> all reflections are conjugate, as reflections correspond to Sylow 2-subgroups. | *In D<sub>6</sub> all reflections are conjugate, as reflections correspond to Sylow 2-subgroups. | ||
| − | [[Image:Application.png]] | + | [[Image:Application.png]] |
| + | |||
| + | |||
| + | |||
| + | |||
*In D<sub>12</sub> reflections no longer correspond to Sylow 2-subgroups, and fall into two conjugacy classes. | *In D<sub>12</sub> reflections no longer correspond to Sylow 2-subgroups, and fall into two conjugacy classes. | ||
| − | [[Image:Application2.png]] | + | [[Image:Application2.png]] |
| − | + | <br> <br> | |
| − | <br> | + | |
<br> | <br> | ||
| Line 129: | Line 131: | ||
== References == | == References == | ||
| − | <br>Sikimeti Ma'u. ''Notes on Sylow's Theorems.'' Retrived from [http://math.berkeley.edu/~sikimeti/SylowNotes.pdf math.berkeley.edu/~sikimeti/SylowNotes.pdf]<br>Alavaro Loustau. ''Latex Tutorial.'' Retreived from [http://omega.albany.edu:8008/Symbols.html | + | <br>Sikimeti Ma'u. ''Notes on Sylow's Theorems.'' Retrived from [http://math.berkeley.edu/~sikimeti/SylowNotes.pdf math.berkeley.edu/~sikimeti/SylowNotes.pdf]<br>Alavaro Loustau. ''Latex Tutorial.'' Retreived from [http://omega.albany.edu:8008/Symbols.html omega.albany.edu:8008/Symbols.html ]<br> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | David A. Craven. ''The Theory of p-Groups. ''Retreived from'' ''[http://people.maths.ox.ac.uk/craven/docs/lectures/pgroups.pdf | ||
| + | Ronald Solomon. ''A Brief Histroy of the Classification of the Finite Simple Groups'' [http://www.ams.org/journals/bull/2001-38-03/S0273-0979-01-00909-0/S0273-0979-01-00909-0.pdf www.ams.org/journals/bull/2001-38-03/S0273-0979-01-00909-0/S0273-0979-01-00909-0.pdf]<br>http://groupprops.subwiki.org/wiki/Regular_p-group ('''I'm not confident we should use this as a reference. It's like usign wikipedia, very frowned upon'''.)<br><br> | ||
[[Category:MA453Fall2013Walther]] | [[Category:MA453Fall2013Walther]] | ||
Revision as of 19:00, 30 November 2013
Mark Rosinski, markrosi@purdue.edu Joseph Lam, lam5@purdue.edu Beichen Xiao, xiaob@purdue.edu
Outline:
Contents
Email the group to see if anyone else is currently making changes before you begin making changes yourself!!!
P-groups
Definitions:
- Let p be a prime p be an integer greater or equal to 0. A p-group is a group of order pn.
- A subgroup of order pk for some k ≥ 1 is called a p-subgroup.
- If |G| = pαm where p does not divide m, then a subgroup of order pα is called a Sylow p-subgroup of G.
Propositions:
If G is a p-group then G contains an element of order p.
- If G is a p-group then Z(G)cannot be equal to {1}
- Let p be a prime and let G be a group of order p2. Then G is abelian.
- If G is a p-group of order pa, then there exists a chain, {1} is contained in N1 contained in N2 contained in...contained in Na-1 contained in Gof normal subgroups of G, such that |Ni|=pi.
All content above and proofs of these Propositions can be found here
Further Information on p-groups:
- Lie Algebras
- A lie ring is a set R with two binary operations - addition and the Lie bracket - such that
- (R,+) is an abelian group;
- Bilinearity: The bracket operation distributes over addition;
- Alternating on the vector space g: [x,x] = 0 for all x in R;
- The Jacobi Identity: [[x,y],z]+[[y,z],x]+[[z,x],y]=0 for all x,y,z in R.
- If F is a field, and R is an F-vector space with a[x,y]=[ax,y] then R is a Lie algebra.
- To every finite p-group one can associate a Lie ring L(G), and if G/G' is abelian then L(G) is actually a lie algebra over the finite field GF(p).
- Proposition: Let φ be an automorphism of the finite p-group G. Then φ induces an automorphism on L(G), and if φ has order prime to p, then the induced automorphism has the same order.
- A lie ring is a set R with two binary operations - addition and the Lie bracket - such that
- Number of Groups
- Let g(n) denote the number of groups of order n.
- i) g(p)=1 for p a prime.
- ii) if p<q, then g(pq)=1 if q is not congruent to 1 mod p, and g(pq)=2 otherwise.
- iii) g(p2)=2.
- iv) g(p3)=5.
- Let g(n) denote the number of groups of order n.
From this we can see that the number of groups of order n depends more on the prime structure then on its size.
Look at this table to help explain this notion:
All content of Lie Algebras and Number of groups from this page can be found from here as well as additional information on these topics.
Automorphism Groups of order pn
Propositions:
- Let G denote the elementary abelian group of order pn. Then $ Aut(G)\cong GL_{n}(p) $, the group of n x n matrices over GF(p).
- Let G denote the cyclic group of order n. Then Aut(G) is abeilan, and has order φ(n), where φ denotes Euler's φ-fuction.
- Let G be a cyclic p-group with p odd, and write A=Aut(G). Then A is cyclic.
All information from this section is available from here as well as further information and proofs of these propositions on Automorphism Groups of order pn.
Regular p-groups
Definitons:
- For every $ a, b \in G $ there exists $ c \in [<a,b>,<a,b>] $ such that a^p b^p = (ab)^p c^p
- For every $ a, b \in G $ there exist $ c_i \in [<a,b>,<a,b>] $ such that $ a^p b^p = (ab)^p c^p _1 c^p _2 . . . c^p _i $
- For evert $ a, b \in G $ and every positive integer n there exist elements $ c_i \in [<a,b>,<a,b>] $ such that $ a^q b^q = (ab)^q c^q _1 c^q _2 . . . c^q _i $ where q = pn
Sylow's Theorems
Notation:
Sylp(G) = the set of Sylow p-subgroups of G
np(G)= the # of Sylow p-subgroups of G =|Sylp(G)|
Theorems:
Let G be a group of order pαm, where p is a prime, m≥1, and p does not divide m. Then:
- Sylp(G) cannot be the empty set.
- All Sylow p-subgroups are conjugate in G. To expand, if P1 and P2 are both Sylow p-subgroups, then there is some g in G such that P1=gP1g-1. In particular, np(G)=(G:NG(P)).
- Any p-subgroup of G is contained in a Sylow p-subgroup
- np(G) is congruent to 1 mod p.
All content from this section and proofs of these Theorems can be found here
Application of Sylow theorems
- In D6 all reflections are conjugate, as reflections correspond to Sylow 2-subgroups.
- In D12 reflections no longer correspond to Sylow 2-subgroups, and fall into two conjugacy classes.
Extra Information
For students looking for extensive history on p-groups, Sylow's Theorems and finite simple groups in general you can find this information here
References
Sikimeti Ma'u. Notes on Sylow's Theorems. Retrived from math.berkeley.edu/~sikimeti/SylowNotes.pdf
Alavaro Loustau. Latex Tutorial. Retreived from omega.albany.edu:8008/Symbols.html
David A. Craven. The Theory of p-Groups. Retreived from [http://people.maths.ox.ac.uk/craven/docs/lectures/pgroups.pdf
Ronald Solomon. A Brief Histroy of the Classification of the Finite Simple Groups www.ams.org/journals/bull/2001-38-03/S0273-0979-01-00909-0/S0273-0979-01-00909-0.pdf
http://groupprops.subwiki.org/wiki/Regular_p-group (I'm not confident we should use this as a reference. It's like usign wikipedia, very frowned upon.)