| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
We all "understand" what the number 1 is. Right? How do you really explain what that is to a smart person that has never heard of it? | We all "understand" what the number 1 is. Right? How do you really explain what that is to a smart person that has never heard of it? | ||
| − | There is a mathematical way of doing it, through set theory. Discuss a little how that goes, how you define addition, and so on. | + | There is a mathematical way of doing it, through set theory. Discuss a little how that goes, how you define addition, and so on. |
| − | '''A Brief History on Natural Numbers''' | + | '''A Brief History on Natural Numbers''' |
| − | As most of us know, natural numbers are the numbers that we use to count (1, 2, 3, …). But, where did these numbers come from? | + | As most of us know, natural numbers are the numbers that we use to count (1, 2, 3, …). But, where did these numbers come from? Whether or not to include 0 has been debated throughout history. Zero was included to make the set more “complete.” This was because 0 represents an empty set. We said before that natural numbers are counting numbers. If you do not count any, you have 0 (an empty set). Whether or not 0 is included in the set of natural numbers depends on the field of mathematics, but most define the set starting at 1. |
| − | Whether or not to include 0 has been debated throughout history. Zero was included to make the set more “complete.” This was because 0 represents an empty set. | + | |
| − | ''' | + | '''A Few Definitions''' |
| − | There are many ways to define the addition of natural numbers: recursion, induction, set theory. However, for recursion and induction, we must look at the basic axiom of mathematics that a number, | + | There are a few things that would be helpful in knowing in order to fully understand how we plan on defining the number "1". |
| − | + | ||
| − | Set theory on the other hand defines “0” so that defining “1” becomes easier. Peano axioms, which states that | + | '''Sets'''- There is no mathematical way of defining sets, but we start by defining sets as a collection of objects. These objects are called "elements". Sets are usually denoted by curly brackets: { } with the elements of the set inside the curly brackets. |
| + | |||
| + | Ex. Let's say we have a set of fruits, with fruits being our elements, we would write the set as: | ||
| + | |||
| + | {apples, bananas, oranges, pears, grapes, tomato} | ||
| + | |||
| + | However, it is possible that set could have no elements in which case we denote it as: ∅. | ||
| + | |||
| + | We call this an empty set. It is also possible to have a set of sets.<br> | ||
| + | |||
| + | Let's say we have a set of food, containing a set of fruit, vegetables, and meat. | ||
| + | |||
| + | { fruit, vegetables, meat } can also be written as: | ||
| + | |||
| + | { {apples, bananas, oranges, pears, grapes, tomatoes}, {spinach, broccoli, carrots, peas, tomatoes}, {chicken, beef, pork, fish, venison} }.<br> | ||
| + | |||
| + | '''Union''' - The union of a set is a set that contains elements in one set or the other. This is denoted by the union symbol: ∪ | ||
| + | |||
| + | Let's take a look at the example below: | ||
| + | |||
| + | [[Image:Union.png]] | ||
| + | |||
| + | In this case we are looking at the union of fruits and vegetables or, with the symbols: fruits ∪ vegetables. | ||
| + | |||
| + | If we go from our definition, the union of these two sets would be elements that are in fruits or elements that are in vegetables, but we want to be careful and count each element once. So the set fruits ∪ vegetables would contain: | ||
| + | |||
| + | {apples, bananas, oranges, pears, grapes, tomatoes, spinach broccoli, carrots, peas, tomatoes} | ||
| + | |||
| + | But since tomatoes are both in fruits and vegetables, we can remove one of tomatoes to create the following set: | ||
| + | |||
| + | {apples, bananas, oranges, pears, grapes, tomatoes, spinach broccoli, carrots, peas}. | ||
| + | |||
| + | '''Set Theory''' - Set theory is the application of ideas like unions and sets to come up with theorems/axioms about other mathematical ideas. | ||
| + | |||
| + | '''Defining Addition of Natural Numbers''' | ||
| + | |||
| + | There are many ways to define the addition of natural numbers: recursion, induction, set theory. However, for recursion and induction, we must look at the basic axiom of mathematics that a number, n, added to zero, is still n, or with the symbols: | ||
| + | |||
| + | n + 0 = n | ||
| + | |||
| + | Set theory on the other hand defines “0” so that defining “1” becomes easier. '''Peano axioms''', which states that n+0 =n, can be derived from set theory of natural numbers. These axioms are really helpful when it comes to defining the natural numbers as a whole, especially since a lot of mathematics is based off of this. The definition of “1” starts from the definition of zero, defined by John von Neumann, as an empty set, which can be written as 0 = ∅. What is interesting is that there is no formal proof/definition of "0" besides assuming that 0 = ∅, upon which the rest of this proof is based on and many other axioms are based on, including the previously mentioned '''Peano axioms'''. | ||
| + | |||
| + | By defining "1", we can then define the other numbers. Von Neumann also defines a function, s(n), where s is the successor function. The successor function is defined as s(n) = n+1. So if we use this idea of succession, we can define our successor function such that s(n) = n ∪ {n}. This successor function is especially useful in defining the natual numbers with respect to set theory because it allows us to cover the full set of natural numbers. | ||
| + | |||
| + | '''Proof Using Set Theory''' | ||
| + | |||
| + | Using Set Theory, we are able to construct a proof for defining the Natural numbers. The proof starts by defining zero in terms of sets and building from there.<br> We can let 0:=∅ which indicates zero is denoted as the empty set.<br>From there using the Successor function and the axiom of infinity we are able to state that if 0:={ } then:<br>1 = {0} = {{ }}<br>From there we continue with the next natural number two and state:<br>2 = {0, 1} = {0, {0}} = {{ }, {{ }}}<br>And so on:<br>3 = {0, 1, 2} = {0, {0}, {0, {0}}} ={{ }, {{ }}, {{ }, {{ }}}} | ||
| + | |||
| + | n = {0, 1, 2, ..., n−2, n−1} = {0, 1, 2, ..., n−2,} ∪ {n−1} = {n−1} ∪ (n−1) = S(n−1) | ||
| + | |||
| + | Set theory allows us to define natural numbers in set form and gives us a formal definition to how we are able to state what is 1, 2, 3, etc. all the way up to n.<br><br> | ||
| + | |||
| + | [[Image:Emptyset.png]] | ||
| + | |||
| + | The easiest way to describe this is by saying that if you have nothing and and a collection of nothing, you still have a collection of nothing. Since we defined that nothing is the same as 0, we can state that we have a collection of 0, which we write as {0}. | ||
| + | |||
| + | 0 = ∅<br>1 = s(0) = s(∅) = ∅∪ {∅} = {∅} = {0}<br>2 = s(1) = s({0}) = {0}∪{ {0} } = {0, {0}} = {0,1} | ||
| + | |||
| + | So by this definition, via set theory, we can define "1" as a set containing only a single element, which we defined as 0.<br> | ||
| + | |||
| + | <u>'''Sources: '''</u> | ||
| + | |||
| + | http://en.wikipedia.org/wiki/Natural_number<br>http://en.wikipedia.org/wiki/Addition<br>http://en.wikipedia.org/wiki/Peano_axioms#Addition<br>http://en.wikipedia.org/wiki/Successor_function | ||
| + | |||
| + | <br> | ||
[[2014 Spring MA 375 Walther|Back to MA375 Spring 2014]] | [[2014 Spring MA 375 Walther|Back to MA375 Spring 2014]] | ||
[[Category:MA375Spring2014Walther]] [[Category:Math]] [[Category:Project]] | [[Category:MA375Spring2014Walther]] [[Category:Math]] [[Category:Project]] | ||
Latest revision as of 13:45, 27 April 2014
We all "understand" what the number 1 is. Right? How do you really explain what that is to a smart person that has never heard of it?
There is a mathematical way of doing it, through set theory. Discuss a little how that goes, how you define addition, and so on.
A Brief History on Natural Numbers
As most of us know, natural numbers are the numbers that we use to count (1, 2, 3, …). But, where did these numbers come from? Whether or not to include 0 has been debated throughout history. Zero was included to make the set more “complete.” This was because 0 represents an empty set. We said before that natural numbers are counting numbers. If you do not count any, you have 0 (an empty set). Whether or not 0 is included in the set of natural numbers depends on the field of mathematics, but most define the set starting at 1.
A Few Definitions
There are a few things that would be helpful in knowing in order to fully understand how we plan on defining the number "1".
Sets- There is no mathematical way of defining sets, but we start by defining sets as a collection of objects. These objects are called "elements". Sets are usually denoted by curly brackets: { } with the elements of the set inside the curly brackets.
Ex. Let's say we have a set of fruits, with fruits being our elements, we would write the set as:
{apples, bananas, oranges, pears, grapes, tomato}
However, it is possible that set could have no elements in which case we denote it as: ∅.
We call this an empty set. It is also possible to have a set of sets.
Let's say we have a set of food, containing a set of fruit, vegetables, and meat.
{ fruit, vegetables, meat } can also be written as:
{ {apples, bananas, oranges, pears, grapes, tomatoes}, {spinach, broccoli, carrots, peas, tomatoes}, {chicken, beef, pork, fish, venison} }.
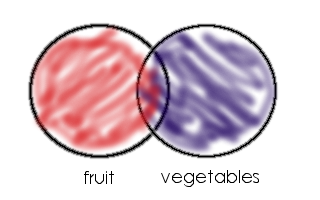
Union - The union of a set is a set that contains elements in one set or the other. This is denoted by the union symbol: ∪
Let's take a look at the example below:
In this case we are looking at the union of fruits and vegetables or, with the symbols: fruits ∪ vegetables.
If we go from our definition, the union of these two sets would be elements that are in fruits or elements that are in vegetables, but we want to be careful and count each element once. So the set fruits ∪ vegetables would contain:
{apples, bananas, oranges, pears, grapes, tomatoes, spinach broccoli, carrots, peas, tomatoes}
But since tomatoes are both in fruits and vegetables, we can remove one of tomatoes to create the following set:
{apples, bananas, oranges, pears, grapes, tomatoes, spinach broccoli, carrots, peas}.
Set Theory - Set theory is the application of ideas like unions and sets to come up with theorems/axioms about other mathematical ideas.
Defining Addition of Natural Numbers
There are many ways to define the addition of natural numbers: recursion, induction, set theory. However, for recursion and induction, we must look at the basic axiom of mathematics that a number, n, added to zero, is still n, or with the symbols:
n + 0 = n
Set theory on the other hand defines “0” so that defining “1” becomes easier. Peano axioms, which states that n+0 =n, can be derived from set theory of natural numbers. These axioms are really helpful when it comes to defining the natural numbers as a whole, especially since a lot of mathematics is based off of this. The definition of “1” starts from the definition of zero, defined by John von Neumann, as an empty set, which can be written as 0 = ∅. What is interesting is that there is no formal proof/definition of "0" besides assuming that 0 = ∅, upon which the rest of this proof is based on and many other axioms are based on, including the previously mentioned Peano axioms.
By defining "1", we can then define the other numbers. Von Neumann also defines a function, s(n), where s is the successor function. The successor function is defined as s(n) = n+1. So if we use this idea of succession, we can define our successor function such that s(n) = n ∪ {n}. This successor function is especially useful in defining the natual numbers with respect to set theory because it allows us to cover the full set of natural numbers.
Proof Using Set Theory
Using Set Theory, we are able to construct a proof for defining the Natural numbers. The proof starts by defining zero in terms of sets and building from there.
We can let 0:=∅ which indicates zero is denoted as the empty set.
From there using the Successor function and the axiom of infinity we are able to state that if 0:={ } then:
1 = {0} = {{ }}
From there we continue with the next natural number two and state:
2 = {0, 1} = {0, {0}} = {{ }, {{ }}}
And so on:
3 = {0, 1, 2} = {0, {0}, {0, {0}}} ={{ }, {{ }}, {{ }, {{ }}}}
n = {0, 1, 2, ..., n−2, n−1} = {0, 1, 2, ..., n−2,} ∪ {n−1} = {n−1} ∪ (n−1) = S(n−1)
Set theory allows us to define natural numbers in set form and gives us a formal definition to how we are able to state what is 1, 2, 3, etc. all the way up to n.
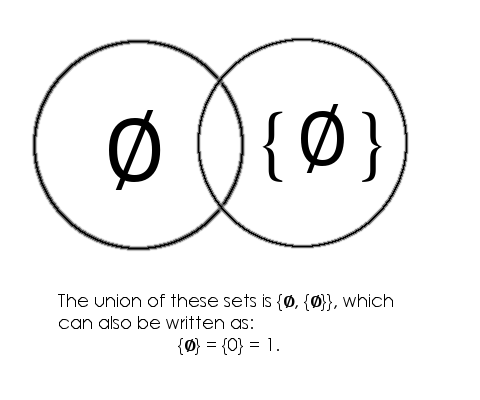
The easiest way to describe this is by saying that if you have nothing and and a collection of nothing, you still have a collection of nothing. Since we defined that nothing is the same as 0, we can state that we have a collection of 0, which we write as {0}.
0 = ∅
1 = s(0) = s(∅) = ∅∪ {∅} = {∅} = {0}
2 = s(1) = s({0}) = {0}∪{ {0} } = {0, {0}} = {0,1}
So by this definition, via set theory, we can define "1" as a set containing only a single element, which we defined as 0.
Sources:
http://en.wikipedia.org/wiki/Natural_number
http://en.wikipedia.org/wiki/Addition
http://en.wikipedia.org/wiki/Peano_axioms#Addition
http://en.wikipedia.org/wiki/Successor_function