Any integer factors, more or less uniquely, into prime numbers. Does this question make sense for real numbers? What about numbers of the form a+b*i where i^2=-1 and a,b are integers? What about numbers of the form a+b*root(N) where a,b,N are integers?
(Possible appendix: What does this concept have to do with Fermat's Last theorem, and what does FLT say anyway?)
Unique Factorization:
First, what is Unique Factorization? The unique factorization theorem is also known as the Fundamental Theorem of Arithmetic which states that all integers greater than 1 are either prime numbers or can be created by multiplying prime numbers.
Mathisfun.com provides a great picture of what this looks like:
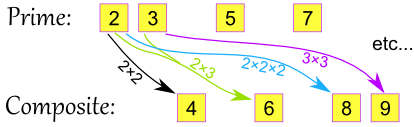
Let's begin with defining what an integer is. An integer consists of all natural numbers (0,1,2,...), includes 0 and all all of the natural numbers of the opposite signs (-1,-2,....). In order to further our understanding of unique factorization, we must also define a prime number. A prime number according to Webster's dictionary is "a number (such as 2, 3, or 5) that can only be exactly divided by itself and by 1". In other words, a prime number is a number with no factors beyond itself or 1.
In this project, we will be explaining how every integer greater than 1 factors into a unique set of prime numbers, and later we will discuss whether this concept with also suffice for real, imaginary and/or rational numbers as well.
Fermat’s Last Theorem
Fermat’s Last Theorem states that for the Diophantine equation x^n + y^n = z^n where x, y, and z are integers has no solutions that are nonzero when n>2.
Background: Around 1637 Fermat claimed to have proven this theorem. He wrote in the margins of one of his books that when n>2 there were no solutions to the Diophantine equation. However, he did not prove his claim. 358 years later Andrew Wiles was able to successfully prove Fermat’s last theorem.
An example of a Proof of n=3: x^3 + y^3 = z^3
x^3 -1=(x-1)(x-t)(x-t^2) where t=e^2πi/3 Let x=x/y Can be rewritten as (x^3)/(y^3) – 1=(x/y -1)(x/y –t)(x/y –t^2) Now multiply both sides b y^3 and y become –y. Can be rewritten as z^3 = x^3 + y^3 = (x+y)(x+ty)(x+(t^2)y)
By looking at the prime factors of the left side of the above equation, it is impossible for it to equal z^3.
Andrew Wiles came up with an extensive proof for all “n” in 1994 and it was later published in 1995.
Resources: Rabinoff, J. (n.d.).Retrieved April 26, 2014, from http://people.math.gatech.edu/~jrabinoff6/mathcamp/lectures.pdf
http://www.mathsisfun.com/numbers/fundamental-theorem-arithmetic.html

