| Line 15: | Line 15: | ||
'''A basic example of how to use the theorems is a simple two-coloring of a square. <br>''' | '''A basic example of how to use the theorems is a simple two-coloring of a square. <br>''' | ||
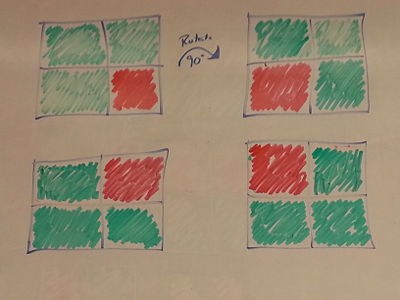
| − | '''Step 1: | + | '''Step 1: The six unique graphs are shown for a two-coloring of a 2x2 square:'''<br> |
| − | [[Image:TwoColoringCombinations.jpg|left|800x600px|All possible two coloring combinations of a 2x2 square.]] | + | <br> |
| + | |||
| + | <br> | ||
| + | |||
| + | [[Image:TwoColoringCombinations3.2.jpg|400x300px|Six unique two colorings of a 2x2 square.]] | ||
| + | |||
| + | [[Image:TwoColoringCombinations2.jpg|400x300px|Isomorphisms of a 2x2 square.]] | ||
| + | |||
| + | <br> | ||
| + | |||
| + | '''Step 2: Finding the isomorphic graphs for each unique graph:''' | ||
| + | |||
| + | This provides a lists of all the different colorings possible. | ||
| + | |||
| + | <br> | ||
| + | |||
| + | <br> | ||
| + | |||
| + | [[Image:TwoColoringCombinations.jpg|left|800x600px|All possible two coloring combinations of a 2x2 square.]]It can also be shown in an "alphabitcal" notation: | ||
{| width="200" border="1" cellspacing="1" cellpadding="1" | {| width="200" border="1" cellspacing="1" cellpadding="1" | ||
| Line 42: | Line 60: | ||
|} | |} | ||
| − | <br> | + | <br> <br> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | <br> | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | '''Definitions:''' | + | <br> '''Definitions:''' |
*'''Burnside-'''The lemma counts the number of orbits of a set X acted upon by a group G. # of Orbits = (1/|G|) Sum over G |x^g|. Where x^g is an element of x such that g(x) = x, and |x^G| is the number of elements that fit this defintion. | *'''Burnside-'''The lemma counts the number of orbits of a set X acted upon by a group G. # of Orbits = (1/|G|) Sum over G |x^g|. Where x^g is an element of x such that g(x) = x, and |x^G| is the number of elements that fit this defintion. | ||
Revision as of 13:26, 20 April 2014
We discuss in class colorings of graphs, where adjacent vertices have different colors. Suppose you took the graph to be a polygon and allowed the graph to be reflected and rotated. How many different colorings do you get?
Contents
Outline/Title?
Introduction
In graph theory, it is sometimes necessary to find the number of ways to color the vertices of a polygon. Two theorems that work together to solve this problem are the Polya theorem and Burnside theorem.
Example 1: Square
A basic example of how to use the theorems is a simple two-coloring of a square.
Step 1: The six unique graphs are shown for a two-coloring of a 2x2 square:
Step 2: Finding the isomorphic graphs for each unique graph:
This provides a lists of all the different colorings possible.
| gggg | gggr | ggrg | rggg |
| grgg | ggrr | rgrg | rrgg |
| grrg | rgrr | grrr | rrgr |
| rrrg | rrrr | grrg | rggr |
Definitions:
- Burnside-The lemma counts the number of orbits of a set X acted upon by a group G. # of Orbits = (1/|G|) Sum over G |x^g|. Where x^g is an element of x such that g(x) = x, and |x^G| is the number of elements that fit this defintion.
- Polya-Applies this to colors.
'
'Formula:
- show formula
- breakdown of each element
- relate back to example 1
Proof:
References and Additional Information
For further reading on the Polya theorem:
http://arxiv.org/pdf/1001.0072.pdf
http://math.berkeley.edu/~mbaker/Tucker.pdf
http://www.whitman.edu/mathematics/SeniorProjectArchive/2012/Huisinga.pdf