| Line 46: | Line 46: | ||
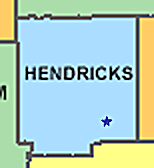
Then in our function, we could just look for some straight line coming out from the point we're interested in (commonly called a ray) which intersects the outline of the county. So our function would just involve looping through each segment in a county's outline and seeing if the ray intersects that segment. If such an intersecting ray does exist, the point is inside. If not, it's outside. This would be wonderfully simple if it were completely true, but what if the counties are more complicated? If you think for a bit, you can surely find a counterexample. To prove me wrong, you need to find a hypothetical county in which my function would return the wrong answer. One example is Vanderburgh county in Indiana: | Then in our function, we could just look for some straight line coming out from the point we're interested in (commonly called a ray) which intersects the outline of the county. So our function would just involve looping through each segment in a county's outline and seeing if the ray intersects that segment. If such an intersecting ray does exist, the point is inside. If not, it's outside. This would be wonderfully simple if it were completely true, but what if the counties are more complicated? If you think for a bit, you can surely find a counterexample. To prove me wrong, you need to find a hypothetical county in which my function would return the wrong answer. One example is Vanderburgh county in Indiana: | ||
| − | [ | + | [[Image:Vanderburgh_county.png]] |
---- | ---- | ||
Revision as of 05:08, 16 March 2013
Contents
The County Problem - A Topological Argument
keyword: tutorial, inside county, closed curve, curve
INTRODUCTION In this tutorial / exploration, I'll talk a little about topology, and a little about programming, with the goal of showing you that thinking mathematically can really get you out of a pickle sometimes.
Contents - TheProblem - A First Try - The Solution - The Code
The problem
The problem we want to solve here is as follows: we want to create a function in some computer language which takes an Indiana longitude and latitude value as input, and returns the county in which this point lies. For example, in Java we would want:
String getCounty( float lat, float lon ) {
//Code here
}
System.out.println( getCounty( 39.162147, -86.529045 ) );
to output "Monroe", because that (39.162147, -86.529045) is in Monroe county.
A first try
At first glance, intuition tells you that this problem should be easy. After all, when one looks at a county and some point in the vicinity of the county, they can immediately tell whether the point is inside or outside of this county. But this mental action of discerning the "insideness", so to speak, of the point, is something we must inspect. What exactly do we do to determine the "insideness" of a point? Imagine we are looking at a county and a point, and set forth at the task of determining its insideness. What is the mental method we use to do this? In the simplest situations, it's extremely easy. Consider, for example, the case of a rectangular county, a somewhat common example:
We can immediately see that the capital is inside the county. But how do we see that? Well, when nagged about a thorough explanation, I'd say that if the capital were outside the county, I could take it and drag it as far away as I like without it ever intersecting the sides of the county. But if I drag the point in any direction from where it's drawn, I'll almost immediately hit a side. Thus the point is inside the county. In other words, if I draw a line from the point in any direction, and it hits a side of the county, then the point is inside the county. So, is it that simple? It certainly suffices for the simplest of counties. Imagine I have the array of points for some county I'm interested in, and it's extremely simple:
//This creates a county which is a 10-sided polygon :)
float two_pi = 2 * 3.1415926;
float[][] myCounty = new float[10][2]
for( i=0; i<10; i++ ) {
float angle = (i / 10) * two_pi;
float x = Math.cos( angle );
float y = Math.sin( angle );
myCounty.push( [x, y] );
}
Then in our function, we could just look for some straight line coming out from the point we're interested in (commonly called a ray) which intersects the outline of the county. So our function would just involve looping through each segment in a county's outline and seeing if the ray intersects that segment. If such an intersecting ray does exist, the point is inside. If not, it's outside. This would be wonderfully simple if it were completely true, but what if the counties are more complicated? If you think for a bit, you can surely find a counterexample. To prove me wrong, you need to find a hypothetical county in which my function would return the wrong answer. One example is Vanderburgh county in Indiana:
The solution
So my function fails, and it's clear that in even more complicated situations, my function would fail almost exclusively:
//Insert picture of crazy Jordan curve
But this approach still provides useful information. Imagine we decide to walk along the ray to freedom. Whether we're inside or outside the county, if we walk along the whole ray, we'll end up outside the county, and we know this. As we walk along this ray, we may never cross a border at all. It's clear in this case that we most certainly did not start inside the county. Thus if we draw a ray out from a point and it makes no intersections with the curve, the point must have been outside it. On the other hand, we also know that if we only cross the border once on our way out, we must have started inside the county! So if we count the number of intersections to be 1, we are positive the point is inside the county. What if there were two intersections? We ended up outside the county, and we crossed the border twice, so we must have gone in the county, and then back out again. In fact, if we cross the border twice at any time, our insideness before is the same as our insideness after. Thus if we find any even number of intersections with the ray, $ 2n, n \in \mathbb{N} $, the insideness at the beginning of your journey is the same as your insideness at the end of your journey, and thus the point was outside the path. Likewise, if we find any odd number of intersections with the ray, $ 2n+1, n \in \mathbb{N} $, the insideness at the beginning of your journey is the same as your insideness just before you cross your last border, and thus the point was inside the path.
This result is what I used to solve the problem:
If the ray intersects the curve an odd number of times, the point is inside. If the number of intersections is even, the point is outside. Thus if we count the number of intersections the ray has with the county's border, we can still find the "insideness" of the point.
The code
Now what's the best way to implement this fact? We are given a point and desire to determine which county in Indiana it belongs. I have a file containing the boundary points of every county in the USA (available for free online, with some Googling). If we give each county an index, 0 - 91, then we can store these points in a large multidimensional array. Let's say I've already figured out how to do that, and the points are in a variable called county_pts. Not only that, but I've stored the names of these counties in an array with the same order, so that we can access them later, county_names. Just so we're clear about what we're talking about
The first thing to note is that this problem is equivalent to the slightly less complicated task of creating a function to determine whether a point lies in a specific county. If we are able to create such a function, call it int inCounty( int county, float lat, float long ), then the function we want would just be:
String getCounty( float lat, float long ) {
//Loop through the counties
for( i = 0; i < counties.length; i++ )
//For each county, check if the point given is in that county
if( inCounty( i, lat, long ) )
//If it is, return the name of that county
return county_names[i];
//If no county is found, return "County not found"
return "County not found.";
}
So we should be ready to go, we just have to write the code-version of our theorem. We draw some ray from the point, and count the number of intersections with the sides of the county. Then we can say whether the point is inside or outside the county just by whether this number is even or odd.
int inCounty( int county, float lat, float long ) {
int count = 0;
for( i = 0; i < county_pts[county].length; i++ ) {
if(
}
}
The solution here is due to a rather fun and at first surprising topological fact. Imagine we have some closed, simple curve in the plane. Here, closed just means that the two ends of the curve meet, and simple means that this curve doesn't intersect itself. In mathematical terms, the curve can be parameterized by a function
$ f: [0, 1] \to \mathbb{ R } $
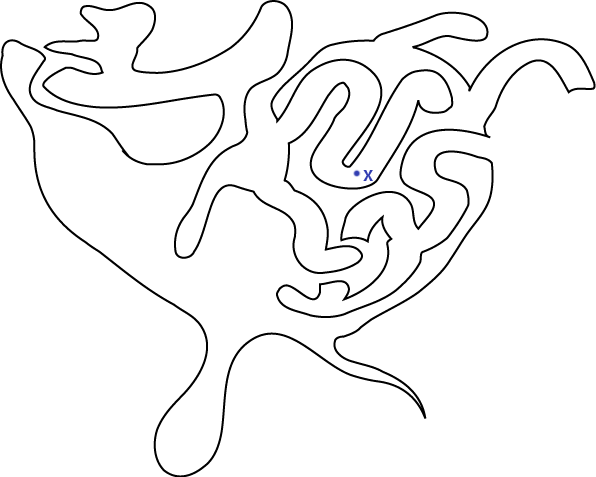
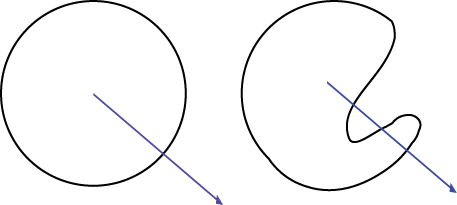
which is continuous (this is what makes it a curve), invective on $ [0, 1) $ (this is what makes it simple), and $ f(0) = f(1) $ (this is what makes it closed). This is called a Jordan Curve. Intuitively, we can think of a Jordan curve as anything we could make with a loop of string on a table, without letting it cross itself. The remarkable fact is that if you have any Jordan curve, which can get pretty complicated, and some point of interest which you'd like to determine whether the point is inside or outside this curve, it's quite simple. Let's say we're interested in the curve below:
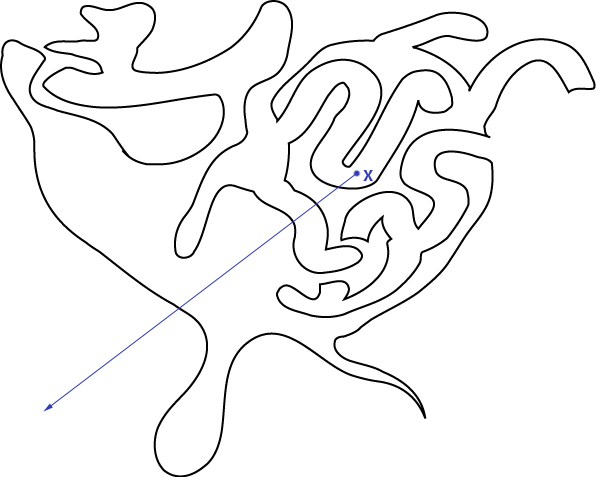
and we'd like to know whether x is inside or outside the curve. Just draw a ray from that point in any direction and count the number of times it intersects the curve:
If the ray intersects the curve an odd number of times, the point is inside. If the number of intersections is even, the point is outside. We can see here that it intersects the sides an even number of times, and we can confirm visually that the point x is indeed outside the curve. That's it! You can easily do some testing of this by drawing crazy Jordan curves (make sure they are both simple and closed) and a random point, and trying to determine the "insideness" of the point. I'll explain in the next section why this statement is true, and maybe you can convince yourself of it if you do some mindful fiddling with Jordan curves. But now I'll show you how we can implement this and solve the original problem.
Now, the first
Why it works
- Explain what a homeomorphism is
Now why does this work? It seems like a magical fact which I just pulled out of my pocket. But the great thing about this particular mathematical fact is that it's something which we can easily argue. So here I'll present the outline of a proof. The idea is that if we were to take a large circle, we can bend continuously, and with rather strict rules, into an arbitrary simple, closed curve (a curve which is simple and curved is commonly called a Jordan Curve). These strict rules preserve a specific property of the curve which corresponds to the insideness of the chosen point.
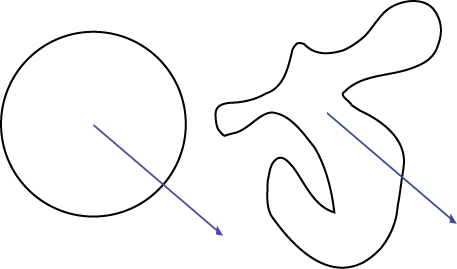
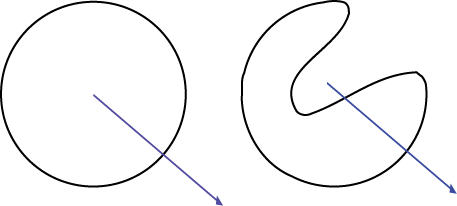
Imagine you start with some arbitrary curve in the plane, and you're interested in whether a point is inside or outside the curve:
Now imagine you draw a ray from that point in an arbitrary direction in the plane, and that we focus on the number of intersections that line makes with the sides or the curve:
It is not yet clear what the relationship is between the number of intersections and the insideness of the point, but we can try to reduce the situation to a simpler situation. Imagine the various deformations of the curve which preserve insideness and the effect these has on the number of intersections:
//Copied out of here
Note then that the first two homeomorphisms and the inverse of the second preserve insideness. Because every Jordan curve is homeomorphic to the unit circle, we know there exists a homeomorphism between the two, and it is easy to see that this homeomorphism can be broken down into type 1, type 2, type 3, and the inverse of type 2 and type 3 homeomorphisms.
Theorem:
A point is inside a closed curve ""if and only if"" any ray going away from this point intersects the curve an odd number of times.
Outline of proof:
First note that every closed simple loop, or Jordan curve is homeomorphic to the unit circle. Then it easily follows that given an arbitrary curve in the plane, and a point within it, there exists a "smooth transformation" of the curve into the unit circle about that point. This is evident because given some coordinate system, there exists a smooth mapping between the curve and the unit circle, and there then exists a linear transformation of this unit circle about the origin into a unit circle about the point in question.
Once we are aware that there exists this smooth transition we can focus on how this property, the number of intersections of a ray with the curve, changes with time t. The trick is that there are only finitely many states of the homeomorphism in [0, 1] on which the intersection number changes. We are able to characterize these as follows:
Type 1: A homeomorphism which preserves both number of intersections and insideness
Type 2: A homeomorphism which preserves insideness, but not number of intersections
Type 3: A homeomorphism which preserves neither number of intersections or insideness
I will denote these functions as $ T_{i} $ and their inverses, also homeomorphisms by definition, by $ T^-1_{i} $. Then intuitively you can convince yourself that any homeomorphism can be illustrated as a combination of these six functions (five if you account that $ T_{i} = T^-1_{i} $) in sequence. The rigorous proof of this fact involves differential geometry, but if you can convince yourself that this is true for the string analogy, that's all you need to convince yourself this is true in any real life situation. So let's introduce some notation that'll be helpful. We have some continuous series of functions, $ f_{t}: [0,1) \to \mathbb{R}^2 $, which represents the homomorphism between the given curve and the unit circle centered about the point in question.