Introduction
There are three parts in this slecture. The first part introduces piano key frequencies, which aim to help students to better understand the materials of hw02. The second part talks about some properties of the ROC for the z-transform to help students better understand the materials related to z-transforms that discussed during class. The third part is to show different types of truncation windows and some basic analysis of them.
Part 1
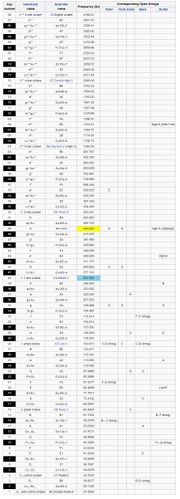
A piano keyboard typically contains keys for playing the twelve notes of the Western musical scale, with a combination of larger, longer keys and smaller, shorter keys that repeats at the interval of an octave. Here is the list containing the key numbers, names and their corresponding frequencies (shown below). When the A440 pitch standard is used to tune a musical instrument, Middle C has a frequency around 261.6 Hz. Middle C is designated C4 in scientific pitch notation because of the note’s position as the fourth C key on a standard 88-key piano keyboard. The frequency of the nth key is calculated from the equation: f(n) = 2^((n-49)/12) * 440 Hz (a’ = A4 = A440 is the 49th key on the idealized piano)
Part 2
There are a number of properties of the region of convergence for the z-transform.
1. The ROC of X(z) consists of a ring in the z-plane centered about the origin.
2. The ROC does not contain any poles.
3. If x[n] is of finite duration, then the ROC is the entire z-plane, except possibly z=0 and/or z = infinite
4. If x[n] is a right-sided sequence, and if the circle |z| = r0 is in the ROC, then all finite values of z for which |z| > r0 will also be in the ROC.
5. If x[n] is a left-sided sequence, and if the circle |z| = r0 is in the ROC, then all values of z for which 0<|z|< r0 will also be in the ROC.
6. If x[n] is two sided, and if the circle |z| = r0 is in the ROC, then the ROC will consist of a ring in the z-plane that includes the circle |z| = r0.
7. If the z-transform X(z) of x[n] is rational, then its ROC is bounded by poles or extends to infinity.
8. If the z-transform X(z) of x[n] is rational, and if x[n] is right sided, then the ROC is the region in the z-plane outside the outermost pole. Furthermore, if x[n] is causal, then the ROC also includes z = infinity.
9. If the z-transform X(z) of x[n] is rational, and if x[n] is left sided, then the ROC is the region in the z-plane inside the innermost nonzero pole. In particular, if x[n] is anticausal (i.e., if it is left sided and equal to 0 for n > 0), then the ROC also includes z = 0.
Causality
1. A discrete-time LTI system is causal if and only if the ROC of its system function is the exterior of a circle, including infinity.
2. A discrete-time LTI system with rational system function H(z) is causal if and only if: (a) the ROC is the exterior of a circle outside the outermost pole; and (b) with H(z) expressed as a ratio of polynomials in z, the order of the numerator cannot be greater than the order of the denominator.
Stability
1. An LTI system is stable if and only if the ROC of its system function H(z) includes the unit circle, |z| = 1.
2. A causal LTI system with rational system function H(z) is stable if and only if all of the poles of H(z) lie inside the unit circle.
Part 3
We can truncate an ideal filter’s impulse response by using different windowing functions. In lab 7a and lab 7b, some truncation windows were introduced, such as, the rectangular window, the hanning window, the hamming window and the blackman window. Here we will discuss the characters of these windows and some other types of truncation windows.
Rectangular window: w(n) = 1
It has excellent resolution characteristics for sinusoids of comparable strength, but it is a poor choice for sinusoids of disparate amplitudes.
Hanning window: w(n) = 0.5*(1 – cos(2*pi*n/(N-1)))
The ends of the cosine just touch zero, so the side-lobes roll off at about 18 dB per octave.
Hamming window: w(n) = 0.54 – 0.46*cos(2*pi*n/(N-1))
The window is optimized to minimize the maximum side lobe, giving it a height of about one-fifth that of the Hann window.
Hanning and Hamming windows are commonly used in narrowband applications, such as the spectrum of a telephone channel.
Blackman window: w(n) = 0.42 – 0.5*cos(2*pi*n/(N-1)) + 0.08*cos(4*pi*n/(N-1))
Cosine window: w(n) = sin(pi*n/(N-1))
A cosine window convolved by itself is known as the Bohman window.
Gaussian window: w(n) = exp(-0.5*((n-(N-1)/2)/( δ*(N-1)/2))^2) δ <= 0.5
Exponential window: w(n) = exp(-|n - (N-1)/2|/τ)
τ is the time constant of the function. The exponential function decays approximately 8.69 dB per time constant. This means that for a targeted decay of D dB over half of the window length, the time constant τ is given by τ = N/2 * 8.69/D
Lanczos window: w(n) = sinc(2*n/(N-1) - 1)
1. Used in Lanczos resampling
2. Sinc(x) is defined as sin(pi*x)/(pi*x) for the Lanczos window
3. Also known as a sinc window, because: w0 (n) = sinc(2*n/(N-1)) is the main lobe of a normalized sinc function.
Reference
C (musical note), Wikipedia, retrieved from: https://en.wikipedia.org/wiki/C_%28musical_note%29
Piano key frequencies, Wikipedia, retrieved from: https://en.wikipedia.org/wiki/Piano_key_frequencies
Musical keyboard, Wikipedia, retrieved from: https://en.wikipedia.org/wiki/Musical_keyboard
The Region of Convergence for the z-Transform, The Z-TRANSFORM, retrieved from: https://engineering.purdue.edu/~mikedz/ee301/OW_Chap10_ZT_PartI.pdf
Analysis and Characterization of LTI Systems Using z-Transforms, The Z-TRANSFORM, retrieved from: https://engineering.purdue.edu/~mikedz/ee301/OW_Chap10_ZT_PartII.pdf
Window function, Wikipedia, retrieved from: https://en.wikipedia.org/wiki/Window_function