Communication Networks Signal and Image processing (CS)
Solution 1:
a) Since $ {{f}_{k}}(\lambda ),\ for\ k=0,\ 1,\ 2 $ are the spectral response functions for the three color outputs of a color camera, and the negative spectrum can’t be produced, they must be nonnegative.
b) Since $ {{r}_{0}}(\lambda ),\ {{g}_{0}}(\lambda ),\ and\ {{b}_{0}}(\lambda ) $ are the CIE color matching functions, they can be both positive and negative. The color matching function are given by
$ \left\{ \begin{matrix} {{r}_{0}}(\lambda )={{r}^{+}}-{{r}^{-}} \\ {{g}_{0}}(\lambda )={{g}^{+}}-{{g}^{-}} \\ {{b}_{0}}(\lambda )=={{b}^{+}}-{{b}^{-}} \\ \end{matrix} \right. $
where $ {{r}^{+}},\ {{r}^{-}},\ {{g}^{+}},\ {{g}^{-}},\ {{b}^{+}},\ {{b}^{-}} $are the response to photons and must be positive, while the color matching function can be negative to produce a saturated color.
c)
$ \begin{align} & F=\left[ \begin{matrix} {{F}_{1}} \\ {{F}_{2}} \\ {{F}_{3}} \\ \end{matrix} \right]=\int\limits_{-\infty }^{\infty }{\left[ \begin{matrix} {{f}_{1}}(\lambda ) \\ {{f}_{2}}(\lambda ) \\ {{f}_{3}}(\lambda ) \\ \end{matrix} \right]}\ I(\lambda )\ d\lambda =\int\limits_{-\infty }^{\infty }{\left( M\left[ \begin{matrix} {{r}_{0}}(\lambda ) \\ {{g}_{0}}(\lambda ) \\ {{b}_{0}}(\lambda ) \\ \end{matrix} \right] \right)}\ I(\lambda )\ d\lambda=M\left( \int\limits_{-\infty }^{\infty }{\left[ \begin{matrix} {{r}_{0}}(\lambda ) \\ {{g}_{0}}(\lambda ) \\ {{b}_{0}}(\lambda ) \\ \end{matrix} \right]}\ I(\lambda )\ d\lambda \right)=M\left[ \begin{matrix} r \\ g \\ b \\ \end{matrix} \right]\ \\ & \Rightarrow\ \left[ \begin{matrix} r \\ g \\ b \\ \end{matrix} \right]={{M}^{-1}}\left[ \begin{matrix} {{F}_{1}} \\ {{F}_{2}} \\ {{F}_{3}} \\ \end{matrix} \right]={{M}^{-1}}_{{}}^{{}}{{F}^{t}} \\ \end{align} $
missed transpose sign on F. It should be [r,g,b]t = M − 1[F1,F2,F3]t.
d)
$ \left[ \begin{matrix} {{x}_{0}}(\lambda ) \\ {{y}_{0}}(\lambda ) \\ {{z}_{0}}(\lambda ) \\ \end{matrix} \right]=M\ \left[ \begin{matrix} {{r}_{0}}(\lambda ) \\ {{g}_{0}}(\lambda ) \\ {{b}_{0}}(\lambda ) \\ \end{matrix} \right],\ where\ M=\left[ \begin{matrix} 0.490 & 0.310 & 0.200 \\ 0.177 & 0.813 & 0.010 \\ 0.000 & 0.010 & 0.990 \\ \end{matrix} \right] $.
Solution 2:
a) Because for real pixels, measured energy from incident photons is always positive.
b) $ {{r}_{0}}(\lambda ),\ {{g}_{0}}(\lambda ),\ and\ {{b}_{0}}(\lambda ) $are the CIE color matching functions, and therefore can be negative. They go negative to match certain reference colors which are beyond the r, g, b primaries.
c)
$ \begin{align} & \int\limits_{-\infty }^{\infty }{\left[ \begin{matrix} {{f}_{1}}(\lambda ) \\ {{f}_{2}}(\lambda ) \\ {{f}_{3}}(\lambda ) \\ \end{matrix} \right]}\left[ \begin{matrix} I(\lambda )d\lambda & I(\lambda )d\lambda & I(\lambda )d\lambda \\ \end{matrix} \right]=\int\limits_{-\infty }^{\infty }{M\left[ \begin{matrix} {{r}_{0}}(\lambda ) \\ {{g}_{0}}(\lambda ) \\ {{b}_{0}}(\lambda ) \\ \end{matrix} \right]}\left[ \begin{matrix} I(\lambda )d\lambda & I(\lambda )d\lambda & I(\lambda )d\lambda \\ \end{matrix} \right] \\ & \Rightarrow \left[ \begin{matrix} \int\limits_{-\infty }^{\infty }{{{f}_{1}}(\lambda )I(\lambda )d\lambda } \\ \int\limits_{-\infty }^{\infty }{{{f}_{2}}(\lambda )I(\lambda )d\lambda } \\ \int\limits_{-\infty }^{\infty }{{{f}_{3}}(\lambda )I(\lambda )d\lambda } \\ \end{matrix} \right]=M\left[ \begin{matrix} \int\limits_{-\infty }^{\infty }{{{r}_{0}}(\lambda )I(\lambda )d\lambda } \\ \int\limits_{-\infty }^{\infty }{{{g}_{0}}(\lambda )I(\lambda )d\lambda } \\ \int\limits_{-\infty }^{\infty }{{{b}_{0}}(\lambda )I(\lambda )d\lambda } \\ \end{matrix} \right]\Rightarrow \left[ \begin{matrix} {{F}_{1}} \\ {{F}_{2}} \\ {{F}_{3}} \\ \end{matrix} \right]=M\left[ \begin{matrix} r \\ g \\ b \\ \end{matrix} \right]\Rightarrow \left[ \begin{matrix} r \\ g \\ b \\ \end{matrix} \right]={{M}^{-1}}\left[ \begin{matrix} {{F}_{1}} \\ {{F}_{2}} \\ {{F}_{3}} \\ \end{matrix} \right] \\ \end{align} $
d) $ \begin{align} \left[ \begin{matrix} r \\ g \\ b \\ \end{matrix} \right]={{M}^{-1}}\left[ \begin{matrix} {{F}_{1}} \\ {{F}_{2}} \\ {{F}_{3}} \\ \end{matrix} \right] \\ \end{align} $
The student can be more specific on the example of such case. I am not sure what is a good example either. Will consult Professor to figure it out.
Related Problem
1. In a color matching experiment, the three primaries R, G, B are used to match the color of a pure spectral component at wavelength λ. Here the color matching allows for color to be subtracted from the reference color. At each wavelength λ, the matching color is given by
$ \left[ {\begin{array}{*{20}{c}} R, G, B \end{array}} \right] \left[ {\begin{array}{*{20}{c}} r(\lambda)\\ g(\lambda)\\ b(\lambda) \end{array}} \right] $
where r(λ), g(λ), and b(λ) are normalized to 1.
Further define the white point
$ W = \left[ {\begin{array}{*{20}{c}} R, G, B \end{array}} \right] \left[ {\begin{array}{*{20}{c}} r_w\\ g_w\\ b_w \end{array}} \right] $
Let I(λ) be the light reflected from a surface.
a) Calculate (re,ge,be) the tristimulus values for the spectral distribution I(λ) using primaries R,G,B and an equal energy white point.
b) Calculate (rc,gc,bc) the tristimulus values for the spectral distribution I(λ) using primaries R,G,B and white point (rw,gw,bw).
(Refer to ECE637 2004 Final Problem 4.)
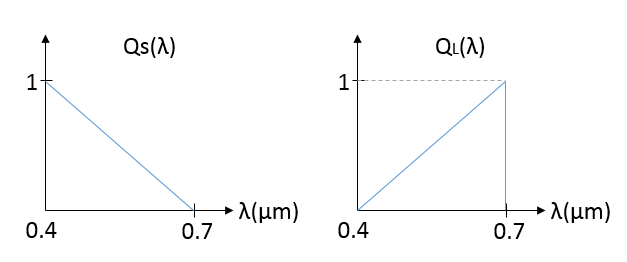
2. Consider the two channel sensors with response function QS(λ) and QL(λ). Suppose that we have two primaries PL(λ) = σ(λ − 0.6) and PS(λ) = σ(λ − 0.5).
Find the color matching function $ \bar{l}(\lambda) $ and $ \bar{s}(\lambda) $ for these two primaries.
(Refer to ECE638 Lecture note 3: Trichromatic theory of color.)