Revision as of 19:01, 26 January 2013

Practice Problem on Conditional Probability

First, watch this video explaining the Mounty Hall Problem

Then use the concept of conditional probability to explain why switching door leads to a probability of success equal to 2/3.

Share your answers below

You will receive feedback from your instructor and TA directly on this page. Other students are welcome to comment/discuss/point out mistakes/ask questions too!

Answer 1

The Monty Hall problem outlined in the above video is analogous to our in-class 'Prisoner's Dilemma', where in the Monty Hall case: car = prisoner is released, goat = prisoner dies.

For the following explanation of this 'problem'/'dilemma', I assume two things:

. one door has car, other two doors have goats (three doors total)
. after the player selects his/her door, the game show host (GSH) will expose one door with a goat that the player has not chosen

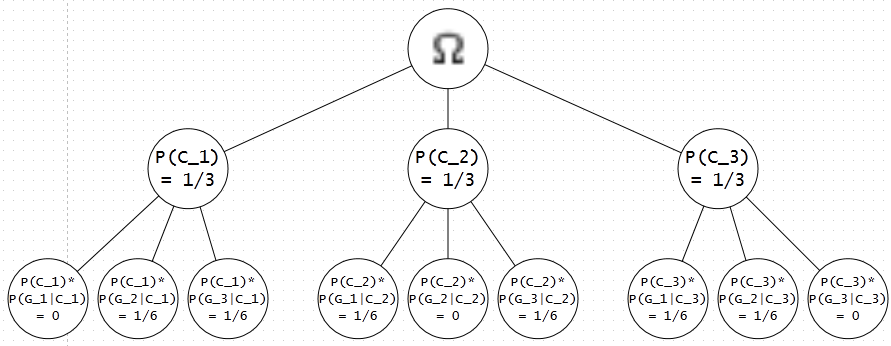
Below you can see the event tree of cases, where 'C'=car and 'G'=goat. Note that all conditional probabilities of $ P(G_i|C_i) \equiv 0 $ since the two events are mutually exclusive for the same door i.

Original Distribution of Probabilities

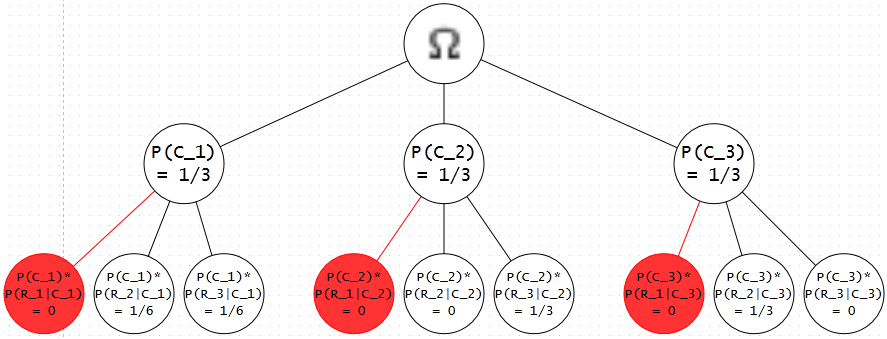
Let's assume that we select door 1 in the hopes that a car sits behind it. Since the GSH is now limited to telling us which of the other two doors contain a goat, we can represent the probability of the GSH revealing ('R') which of the other two doors have a goat with a similar event tree (shown below). Note that sole the modification is that all $ P(G_1|C_i) $ become $ P(R_1|C_i) = 0 $.

Modified Event Tree Representing the Probability GSH will 'R'eveal a Goat

Now, suppose the GSH reveals a goat behind door 3. This removes the possibility of door 3 having a car $ (P(C_3) = 0) $, so working backwards from the given event $ G_3 $, we can calculate the new probabilities of a car existing behind doors 1 and 2 via renormalization. We note that there are 3 possibilities that could have caused the GSH's revelation:

$ P(R_3 \cap C_1) = P(C_1) \cdot P(R_3|C_1) = \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6}  $
$ P(R_3 \cap C_2) = P(C_2) \cdot P(R_3|C_2) = \frac{1}{3} \cdot 1 = \frac{1}{3}  $
$ P(R_3 \cap C_3) \equiv 0 $
$ \therefore P(C_1|R_3) = \frac{P(R_3 \cap C_1)}{P(R_3)} = \frac{\frac{1}{6}}{\frac{1}{6} + \frac{1}{3}} = \frac{\frac{1}{6}}{\frac{1}{2}} = \frac{1}{3}, $
$ P(C_2|R_3) = \frac{P(R_3 \cap C_1)}{P(R_3)} = \frac{\frac{1}{3}}{\frac{1}{6} + \frac{1}{3}} = \frac{\frac{1}{3}}{\frac{1}{2}} = \frac{2}{3} $

Therefore, we observe that the probability of a car existing behind the door we originally chose remains the same ($ \frac{1}{3} $) while the probability of the car existing behind the other unrevealed door has increased to $ \frac{2}{3} $. We can generalize this to a 'Monty Hall Problem' with more than 3 doors: e.g., I determine the resultant probability spread for a 4-door scenario to be $ \frac{1}{12}, \frac{1}{8}, $ and $ \frac{1}{1} $ 'normalized' as before to $ \frac{1}{4}, \frac{3}{8}, $ and $ \frac{3}{8} $ respectively.

Intuitive Method for Solving this Problem

Because we know a goat must exist behind at least one of two doors that player did not choose (since at most one of the two goats can exist behind the chosen door), revealing where a single goat exists does not provide any more information to the chosen door's probability of hiding a car. So assuming door 1 is chosen as in the previous example:

$ P_{initial}(C_1) = P_{final}(C_1) = \frac{1}{3} $

It's also evident that:

$ P_{initial}(C_2) = P_{initial}(C_3) = \frac{1}{3} $

However, if door 3 is revealed to have a goat behind it as in the previous example:

$ P_{final}(C_3) = P(C_3|G_3) \equiv 0 $

By Axiom II:

$ P_{final}(C_1) + P_{final}(C_2) + P_{final}(C_3) = P_{final}(\Omega) = 1 $
$ \therefore 1 - P_{final}(C_1) = P_{final}(C_2) + P_{final}(C_3) = P_{final}(C_2) = \frac{2}{3} $

Answer 2

Write it here.

Answer 3

Write it here.

Back to ECE302 Spring 2013 Prof. Boutin

Back to ECE302