| Line 57: | Line 57: | ||
粉红色的领域是在贝斯决定则下(平等先验概率)第一型错误的概率。红色的领域是固定在.05一下第一型错误的领域 -- 在标准正常分布就是高于1 - .05分位点 = 高于1.644。贝斯的领域同时依赖Ho跟Ha的分布 -- 具体说它依赖Ho密度函数剪Ha密度函数的根。但是如果只想控制第一型错误,只需要看Ho分布。在这个检验,2 > 1.644, 决定规则让选Ha.研究者大概要在他的论文宣告P值(显著性概率)为P(T>2| Ho 正确)= 0.022,也就在是Ho的分布下2以上的曲线下面积。 | 粉红色的领域是在贝斯决定则下(平等先验概率)第一型错误的概率。红色的领域是固定在.05一下第一型错误的领域 -- 在标准正常分布就是高于1 - .05分位点 = 高于1.644。贝斯的领域同时依赖Ho跟Ha的分布 -- 具体说它依赖Ho密度函数剪Ha密度函数的根。但是如果只想控制第一型错误,只需要看Ho分布。在这个检验,2 > 1.644, 决定规则让选Ha.研究者大概要在他的论文宣告P值(显著性概率)为P(T>2| Ho 正确)= 0.022,也就在是Ho的分布下2以上的曲线下面积。 | ||
| − | === | + | === Neyman-Pearson引理 === |
| − | + | 一般在这种假设检验,控制第一型错误的概率是研究者最优先考虑,免得在脆弱的证据下报道肯定的研究成果。统计学家对决定规则的要求是首先固定α = P(第一型错误) 在一定的数量,然后将P(第二型错误)控制在尽可能少的数量。满足此条件的决定规则在统计学中叫做“一致最大功效检验(UMP test)”。Neyman-Pearson引理表明哪种决定规是UMP: | |
| + | |||
| + | Neyman-Pearson引理:决定规则当UMP test的充分必要条件如下: | ||
| + | <blockquote> | ||
| + | <br> | ||
| + | 若<br> | ||
| + | <math> l(X)=\frac{P(T|Ho)}{P(T|Ha)} > k </math><br> | ||
| + | 则选Ho不然选Ha。 | ||
| + | <br> | ||
| + | </blockquote> | ||
| + | 然后 P(第一型错误) 被固定在一位常数α。 | ||
Revision as of 14:41, 2 May 2014
Contents
Hypothesis Testing
模式识别 的目标是将新观察的特征向量进行分类。为了进行分类的决定,需要通过魔钟判决规则(decision rule)。在 统计学模式识别 一般假设特征向量是个随机变量“X”,又有个概率密度函数或者概率质量函数,并且此函数依赖其分类。如下假设有两个类型:(ω1,ω2), 以便写公式也不失一般性。如此X的概率密度或质量函数是P(X | ωi) (如下称pdf)。每个类型的先验概率写成P(ωi)。
统计学的主要部分之一是假设检验。下面描述假设检验在统计学模式识别的眼神。
贝叶斯(Bayes)判决规则
将gi(X) 是ωi的后验概率(posterior probability)。选ω1或ω2的判决规则为: 如果g1(X) > g2(X),就选ω1, 不然选ω2。据贝斯定理, 判决规则能以 似然比(likelihood ratio)l(X) 表示:
$ \begin{align} & g_1(X) > g_2(X) \\ \Rightarrow & P(\omega_1|X) > P(\omega_2|X) \\ \Rightarrow & \frac{P(X|\omega_1)P(\omega_1)}{P(X)} > \frac{P(X|\omega_2)P(\omega_2)}{P(X)} \\ \Rightarrow & P(X|\omega_1)P(\omega_1) > P(X|\omega_2)P(\omega_2) \\ \Rightarrow & l(X)=\frac{P(X|\omega_1)}{P(X|\omega_2)} > \frac{P(\omega_2)}{P(\omega_1)} = k \end{align} $
k 是个常数,而且由于 P(ω2) = 1 − P(ω1), k 可以看待是先验概率的比值(odds) 。为了评估判决规则的效果,需要计算錯誤的概率。假如 r(X) = m'i'n[g1(X),g2(X)]。贝叶斯错误(Bayes error)定义为:
$ \begin{align} \\ \epsilon & = E(r(X)) = \int min(P(\omega_1)P(X|\omega_1), P(\omega_2)P(X|\omega_2))dX \\ &= P(\omega_1) \int_{R_2}P(X|\omega_1)dX + P(\omega_2) \int_{R_1} P(X|\omega_2)dX \\ &= P(\omega_1)\epsilon_1 + P(\omega_2)\epsilon_2 \end{align} $
以上的Ri 定义为决策规则决定选 ωi的领域,然后 εi 是Li选错的概率。
Neyman-Pearson 测试
统计学模式识别与统计学假设检验之间的关系
如果你曾经上过入门的统计学课,你大概能想起传统的 假设检验. 如下为例子:
一位人类学研究者对一名太平岛部落,认为此部落预期寿命比一般人长。把 μ 定义为此部落预期寿命。全世界人口的预期寿命是67.2年。为了检验他的假设,他从公开记录随机选出了100个讣告作为随机样本,发现样本平均预期寿命是72,样本表春差是15。把 X̄ 定义为样本平均值,样本标准差 S,而且由于两都是来自随机样本,两都是随机变量。由于 然后用如下的假设检验:则选H0不然选Ha.
零假设 (H0): μ − 67.2 = 0
对立假设(Ha): μ − 67.2 > 0
检验统计量: $ T = \frac{\bar{X} - 67.5}{\sqrt{S^{2}/N}} \sim N(0,1) $.
决策规则: 若 $ T < Z_{\alpha} $
如上的 $ \alpha = $ P(判决规则让选Ha | H0正确) = P(第一型错误)。 反而第二型错误是在Ha正确的情况下判决规则依然错误选择H0. 假设以上描述的研究者想要控制$ \alpha $不超越.05。
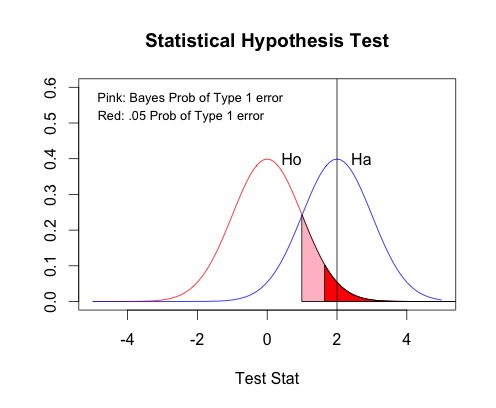
从统计学模式识别的角度上看此假设检验,H0 和 HA是两种类别。随机特征向量是 T,而且条件pdf是高斯分布(标准正常密度分布)。研究者从T抽一次抽样值 t=(72 - 67.2)/(15 * 15 / 100) = 2。 各类的先验概率是平等的。如下图片显示两类的pdf。
粉红色的领域是在贝斯决定则下(平等先验概率)第一型错误的概率。红色的领域是固定在.05一下第一型错误的领域 -- 在标准正常分布就是高于1 - .05分位点 = 高于1.644。贝斯的领域同时依赖Ho跟Ha的分布 -- 具体说它依赖Ho密度函数剪Ha密度函数的根。但是如果只想控制第一型错误,只需要看Ho分布。在这个检验,2 > 1.644, 决定规则让选Ha.研究者大概要在他的论文宣告P值(显著性概率)为P(T>2| Ho 正确)= 0.022,也就在是Ho的分布下2以上的曲线下面积。
Neyman-Pearson引理
一般在这种假设检验,控制第一型错误的概率是研究者最优先考虑,免得在脆弱的证据下报道肯定的研究成果。统计学家对决定规则的要求是首先固定α = P(第一型错误) 在一定的数量,然后将P(第二型错误)控制在尽可能少的数量。满足此条件的决定规则在统计学中叫做“一致最大功效检验(UMP test)”。Neyman-Pearson引理表明哪种决定规是UMP:
Neyman-Pearson引理:决定规则当UMP test的充分必要条件如下:
若
$ l(X)=\frac{P(T|Ho)}{P(T|Ha)} > k $
则选Ho不然选Ha。
然后 P(第一型错误) 被固定在一位常数α。