Contents
Minimum Spanning Tree Methods (MST)
One can find MST using Prim's Algorithm (fast test '57) or Krusal's Algorithm
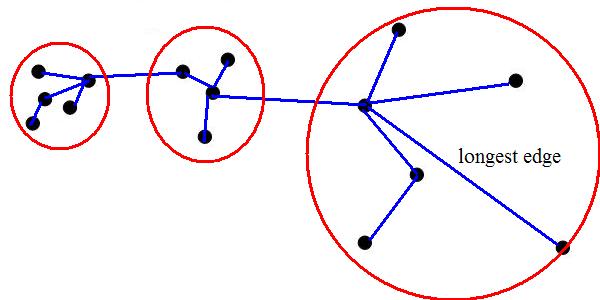
Zahn's clustering algorithm (1971)
- Find MST
- Identify "inconsistent" edges in MST and remove them.
e.g. remove the longest edge
1 edge removed=> 2 clusters
2 edges removed=> 3 clusters
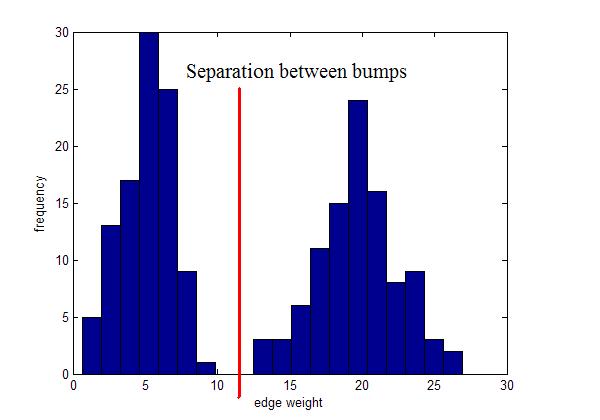
What if you have?
Instead, use "local" inconsistency remove edges significantly larger than their neighborhood edges.
Use for visualization
Visualizations of hierarchical clustering
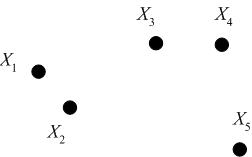
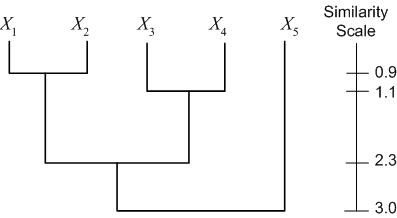
Consider the following set of five 2D data points, which we seek to cluster hierarchically.
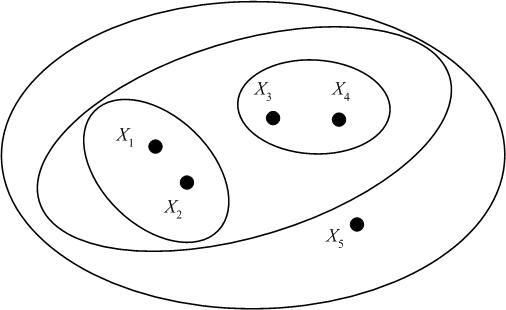
We may represent the hierarchical clustering in various ways. One is by a Venn diagram, in which we circle the data points which belong to a cluster, then subsequently circle any clusters that belong to a larger cluster in the hierarchy.
Another representation is a dendogram. A dendogram represents the clustering as a tree, with clusters that are more closely grouped indicated as siblings "earlier" in the tree. The dendogram also includes a "similarity scale," which indicates the distance between the data points (clusters) which were grouped to form a larger cluster. For the example dataset above (with distances calculated as Euclidian distance), we have the following dendogram:
A third representation of hierarchical clustering is by using brackets. We bracket data points/clusters which are grouped into a cluster in a hierarchical fashion as follows: $ \{\{\{X_1,X_2\},\{X_3,X_4\}\},X_5\} $
Agglomerate Algorithms for Hierarchical Clustering (from Distances)
Reference - Chapter 3.2 from Jain and Dudes ??
Begin with a matrix of pairwise distances:
$ \mathcal{D} = \begin{pmatrix} 0 & d_{1,2} & \cdots & d_{1,d} \\ d_{1,2} & 0 & \ddots & \vdots \\ \vdots & \ddots & \ddots & d_{d-1,d} \\ d_{1,d} & \cdots & d_{d-1,d} & 0 \end{pmatrix} $. For simplicity, assume that the distances are pairwise distinct, and sort distances in increasing order: $ d_1, d_2, \cdots, d_{d/2} $
- Step 1) Begin with clusters $ S_1=\{X_1\}, S_2=\{X_2\}, \cdots, S_d=\{X_d\} $
- Step 2) Find the two nearest clusters $ S_{i_0}, S_{j_0} $ and merge them into a single cluster
- Step 3) Repeat step 2 until the number of clusters reaches a pre-specified number (the number 1 corresponds to a dendogram)
Defining Distances Between Clusters
Option 1: $ {dist}(S_i, S_j) = \min_{X \epsilon S_i, X' \epsilon S_j}{dist}(X, X') $
We call this "Nearest Neighbor Distance." (NOT a distance, since $ {dist}(S_i, S_j)=0 \not{=>} S_i=S_j $)
This distance choice implies a "Nearest Neighbor (NN) clustering algorithm." Note: At each level of clustering, we have a "single-link clustering" with threshold $ t_0= $ distance between the last two clusters that were merged.
Note: If we continue until all $ X_i $'s are linked, we get MST
Option 2: $ {dist}(S_i, S_j) = \max_{X \epsilon S_i, X' \epsilon S_j}{dist}(X, X') $
We call this "Farthest Neighbor (FN) Distance."
Effect: Increase cluster diameters as little as possible.
- At each level of clustering, you get a complete clustering.
Interpretation of NN and FN algorithm (Johnson-King 1967)
- Input proximity matrix $ \mathcal{D}=(d_{i,j}) $
- Decide which cluster distance you will use (NN, FN, ...)
- Set scale = 0
- Begin with $ S_1=\{X_1\},S_2=\{X_2\},\cdots,S_d=\{X_d\} $
- (*) Find $ (S_{i_0},S_{j_0})=\underset{i \not{=} j}{argmin}({dist}(S_i,S_j)) $ from $ \mathcal{D} $
- Merge $ S_{i_0} $ & $ S_{j_0} $
- Update $ \mathcal{D} $ by deleting rows and columns $ i_0 $ and $ j_0 $; add a row and column for $ S_{d+1}=S_{i_0} \cup S_{j_0} $. Fill in new row and column with the chosen cluster distribution.
- If all objects belong to one single cluster, then stop. Else, goto (*).
Generalization (Lance-William 1967):
Update similarity matrix using formula $ {dist}(S_{i_0} \cup S_{j_0}, S_k) = \alpha_{i_0} d(S_{i_0},S_k)+\beta_{j_0} d(S_{j_0},S_k) + \gamma d(S_{i_0},S_{j_0}) + \delta |d(S_{i_0},S_k)-d(S_{j_0},S_k)| $
Related Websites
- Definition
- Kruskal's algorithm
- Prim's algorithm