(→Three crucial questions to answer) |
|||
| Line 32: | Line 32: | ||
<math>I = \sum_{j}P(\omega _j)\log_2P(\omega _j)</math>, when priors are known, else approximate <math>P(\omega _j)</math> by | <math>I = \sum_{j}P(\omega _j)\log_2P(\omega _j)</math>, when priors are known, else approximate <math>P(\omega _j)</math> by | ||
| − | <math>P(\omega _j) = \frac{\# of training patterns in \ | + | <math>P(\omega _j) = \frac{\#\,of\,training\,patterns\,in\,\omega_j}{Total\,\#\,of\,training\,patterns}</math> |
* "Gini Impurity:" | * "Gini Impurity:" | ||
| Line 45: | Line 45: | ||
defined as the "minimum probability that a training pattern is misclassified" | defined as the "minimum probability that a training pattern is misclassified" | ||
| + | |||
| + | Heuristically, want impurity to decrease from one node to its children. | ||
| + | |||
| + | [[Image:node_OldKiwi.jpg]] | ||
| + | |||
| + | We assume that several training patterns are available at node N and they have a good mix of all different classes. | ||
| + | |||
| + | I(N) := impurity at node N. | ||
| + | |||
| + | Define impurity drop at node N as: | ||
| + | <math>\triangle I=I(N)-P_{L}I(N_{L})-(1-P_{L})I(N_{R})</math> | ||
| + | |||
| + | where <math>P_{L}</math> and <math>(1-P_{L})</math> are estimated with training patterns at node N. | ||
Revision as of 09:27, 2 April 2008
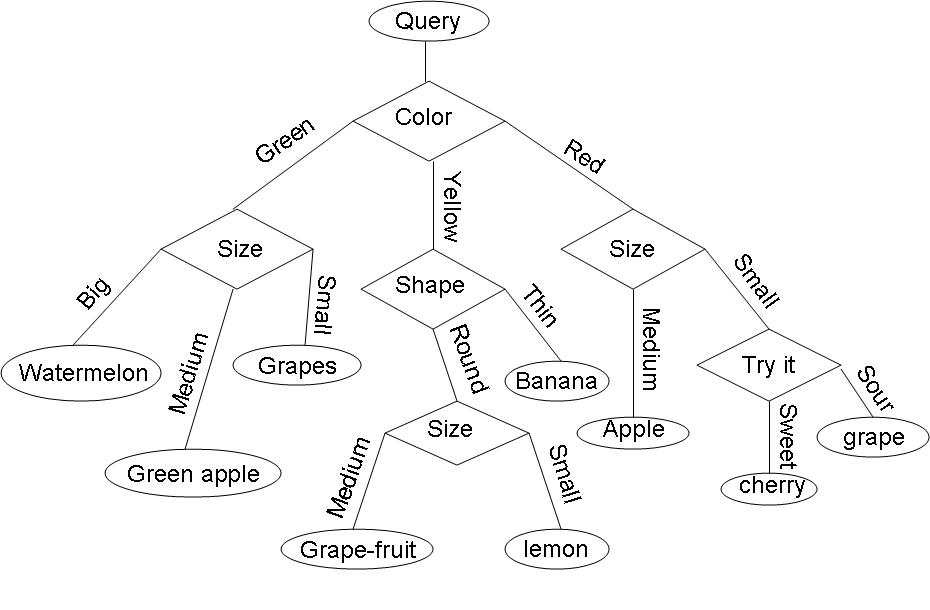
When the number of categories, c is big, decision tress are particularly good.
Example: Consider the query "Identify the fruit" from a set of c=7 categories {watermelon, apple, grape, lemon, grapefruit, banana, cherry} .
One possible decision tree based on simple queries is the following:
- To insert the decision tree example on fruits from class**
Three crucial questions to answer
For constructing a decision tree, for a given classification problem, we have to answer these three questions
1) Which question shoud be asked at a given node -"Query Selection"
2) When should we stop asking questions and declare the node to be a leaf -"When should we stop splitting"
3) Once a node is decided to be a leaf, what category should be assigned to this leaf -"Leaf classification"
We shall discuss questions 1 and 2 (3 being very trivial)
Need to define 'impurity' of a dataset such that $ impurity = 0 $ when all the training data belongs to one class.
Impurity is large when the training data contain equal percentages of each class
$ P(\omega _i) = \frac{1}{C} $; for all $ i $
Let $ I $ denote the impurity. Impurity can be defined in the following ways:
- "Entropy Impurity":
$ I = \sum_{j}P(\omega _j)\log_2P(\omega _j) $, when priors are known, else approximate $ P(\omega _j) $ by $ P(\omega _j) = \frac{\#\,of\,training\,patterns\,in\,\omega_j}{Total\,\#\,of\,training\,patterns} $
- "Gini Impurity:"
$ I = \sum_{i\ne j}P(\omega _i)P(\omega _j) = \frac{1}{2}[1- \sum_{j}P^2(\omega _j) $
Ex: when C = 2, $ I = P(\omega _1)P(\omega _2) $
- "Misclassification Impurity:"
$ I = 1-max P(\omega _j) $
defined as the "minimum probability that a training pattern is misclassified"
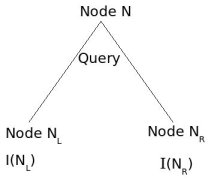
Heuristically, want impurity to decrease from one node to its children.
We assume that several training patterns are available at node N and they have a good mix of all different classes.
I(N) := impurity at node N.
Define impurity drop at node N as: $ \triangle I=I(N)-P_{L}I(N_{L})-(1-P_{L})I(N_{R}) $
where $ P_{L} $ and $ (1-P_{L}) $ are estimated with training patterns at node N.