m |
|||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
We have seen Nearest Neighbor (NN) error rate as the number of samples approaches infinity is <math>P=\int(1-\sum_{i=1}^c P^2(w_i|\vec{x}))p(\vec{x})d\vec{x}</math> | We have seen Nearest Neighbor (NN) error rate as the number of samples approaches infinity is <math>P=\int(1-\sum_{i=1}^c P^2(w_i|\vec{x}))p(\vec{x})d\vec{x}</math> | ||
| Line 91: | Line 89: | ||
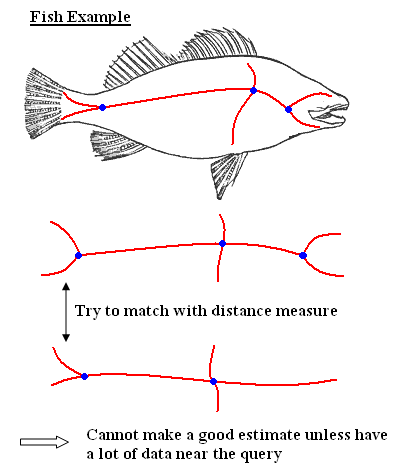
Figure 1 | Figure 1 | ||
| − | + | [[Category:Lecture Notes]] | |
| − | + | ||
| − | + | ||
| − | [ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
Revision as of 21:42, 6 April 2008
We have seen Nearest Neighbor (NN) error rate as the number of samples approaches infinity is $ P=\int(1-\sum_{i=1}^c P^2(w_i|\vec{x}))p(\vec{x})d\vec{x} $
We would like to be able to answer two questions:
1) How good is that in terms of error rate?
2) How does it compare to Bayes, the best error rate we can achieve?
Recall error rate is $ P(e)=\int P(e|\vec{x})p(\vec{x})d\vec{x} $. For all x, Bayes rule yields minimum possible $ P(e|\vec{x})=:P^*(e|\vec{x}) $
Thus, we get the minimum $ P(e)=:P^*=\int P^*(e|\vec{x})p(\vec{x})d\vec{x} $
Claim 1: If $ P^* $ is low, then $ P\approx 2P^* $ (Assumes $ \infty $ number of samples.)
Justification: $ P^*(e|\vec{x})=1-P(w_{max}|\vec{x}) $, where $ w_{max} $ is such that $ P(w_{max}|\vec{x})\geq P(w_j|\vec{x}),\forall j $
So, $ P^* $ low => $ p^*(e|\vec{x}) $ is low for almost every x.
=> $ P(w_{max}|\vec{x}) $ is close to 1 for almost every x.
We have $ P=\int(1-\sum_{i=1}^cP^2(w_i|\vec{x}))p(\vec{x})d\vec{x} $ and for almost every x, $ 1-\sum_{i=1}^cP^2(w_i|\vec{x})\approx 1-P^2(w_{max}|\vec{x})\approx 2(1-P(w_{max}|\vec{x})) $, by Taylor expansion
$ =2(P^*(e|\vec{x}) $
=> $ P\approx\int 2P^*(e|\vec{x})p(\vec{x})d\vec{x}=2P^* $
Claim 2: $ P^*\leq P\leq (2-\frac{c}{c-1}P^*)P^* $
$ P^*\leq P $ obvious can't beat Bayes. In fact, tight!
for RHS inequality $ P=\int(1-\sum_{i=1}^cP^2(w_i|\vec{x}))p(\vec{x})d\vec{x} $
Find the lower bound for this $ \sum_{i=1}^cP^2(w_i|\vec{x}) $
Write $ \sum_{i=1}^cP^2(w_i|\vec{x})=P^2(w_m|\vec{x})+\sum_{i\neq m}P^2(w_i|\vec{x}) $
Minimize this $ \sum_{i\neq m}P^2(w_i|\vec{x}) $
under the constraint $ \sum_{i\neq m}P(w_i|\vec{x})=1-P(w_m|\vec{x})=P^*(e|\vec{x}) $
min is attained when
$ P(w_i|\vec{x})=\frac{P^*(e|\vec{x})}{c-1},\forall i $
So we have
$ \sum_{i=1}^cP^2(w_i|\vec{x})\geq (1-P^*(e|\vec{x}))^2 +(c-1)(\frac {P^*(e|\vec{x})}{c-1})^2 $
$ =(1-P^*(e|\vec{x}))^2 +\frac{(P^*(e|\vec{x}))^2}{c-1} $
$ =1-2P^*(e|\vec{x})+(P^*(e|\vec{x}))^2 +\frac{(P^*(e|\vec{x}))^2}{c-1} $
$ =1-2P^*(e|\vec{x})+\frac{c}{c-1}(P^*(e|\vec{x}))^2 $
Inside the $ \int $
$ 1-\sum_{i=1}^cP^2(w_i|\vec{x}))p(\vec{x})\leq 1-(1-2P^*(e|\vec{x})+\frac{c}{c-1}(P^*(e|\vec{x}))^2) $
$ =2P^*(e|\vec{x})-\frac{c}{c-1}(P^*(e|\vec{x}))^2 $
To get better bound, observe
$ Var(P^*(e|\vec{x})\geq 0 $
$ => \int(p^*(e|\vec x)-p^*)^2p(\vec x)dx\geq 0 $
$ => \int ({p}^{*2}(e|\vec x)-2p*p*(e|\vec x)+{p}^{*2} p(\vec x)dx $
$ => \int {p}^{*2}(e|\vec x)p(x) dx - 2p* \int p*(e| \vec x)p(\vec x)dx + {p}^{*2} \int p(\vec x)dx) \geq 0 $
(where, $ \int p*(e|\vec x)p(\vec x)dx $ should be changed as $ \int p*(e|\vec x)p(\vec x)dx = p* $ )
$ \int {p}^{*2}(e|\vec x)p(\vec x) dx \geq {p}^{*2} $
(This is equal only if variance = 0)
so, $ p\leq \int (2p^*(e| \vec x)- \frac{c}{c-1} {p}^{*2}(e|\vec{x}) ) p(\vec x)dx $
$ = 2 \int p* (e|vec x)p(\vec x) dx - \frac{c}{c-1} \int {p}^{*2}(e|\vec x)p(\vec x) dx $
$ \leq 2p* - \frac {c}{c-1} {p}^{*2} $
$ = (2- \frac{c}{c-1} p* ) p^* $