| Line 42: | Line 42: | ||
In this way, we see that <math> \mathbb{R}^n</math>, <math>\mathbb{Z}^n</math>, <math>\mathbb{C}^n</math> have many natural metrics, but feature could be in some other set, e.g. a discrete set. | In this way, we see that <math> \mathbb{R}^n</math>, <math>\mathbb{Z}^n</math>, <math>\mathbb{C}^n</math> have many natural metrics, but feature could be in some other set, e.g. a discrete set. | ||
| − | + | Example of phi with triangle (Figure 1): | |
[[Image:lec17_rot_tri_OldKiwi.png]] | [[Image:lec17_rot_tri_OldKiwi.png]] | ||
| + | |||
(p1,p2,p3) -> (new p1, new p2, new p3) | (p1,p2,p3) -> (new p1, new p2, new p3) | ||
Revision as of 20:18, 16 March 2008
Nearest Neighbor Classification Rule
- useful when there are several labels
- e.g. fingerprint-based recognition
Problem: Given the labeled training samples: $ \vec{X_1}, \vec{X_2}, \ldots, \vec{X_d} $ $ \in \mathbb{R}^n $ (or some other feature space) and an unlabeled test point $ \vec{X_0} $ $ \in \mathbb{R}^n $.
Classification: Let $ \vec{X_i} $ be the closest training point to $ \vec{X_0} $, then we assign the class of $ \vec{X_i} $ to $ \vec{X_0} $.
What do we mean by closest?
There are many meaning depending on the metric we choose for the feature space.
Definition A "metric" on a space S is a function
$ D: S\times S\rightarrow \mathbb{R} $
that satisfies the following 4 properties:
- Non-negativity $ D(\vec{x_1},\vec{x_2})\geq 0, \forall \vec{x_1},\vec{x_2}\in S $
- Symmetry $ D(\vec{x_1},\vec{x_2})=D(\vec{x_2},\vec{x_1}), \forall \vec{x_1},\vec{x_2}\in S $
- Reflexivity $ D(\vec{x},\vec{x})=0, \forall \vec{x}\in S $
- Triangle Inequality $ D(\vec{x_1},\vec{x_2})+D(\vec{x_2},\vec{x_3})\geq D(\vec{x_1},\vec{x_3}) , \forall \vec{x_1}, \vec{x_2}, \vec{x_3}\in S $
Examples of metrics
Euclidean distance: $ D(\vec{x_1},\vec{x_2})=||\vec{x_1}-\vec{x_2}||_{L_2}=\sqrt{\sum_{i=1}^n ({x_1}^i-{x_2}^i)^2} $
Manhattan distance: $ D(\vec{x_1},\vec{x_2})=||\vec{x_1}-\vec{x_2}||_{L_1}=\sum_{i=1}^n |{x_1}^i-{x_2}^i| $
Minkowski metric: $ D(\vec{x_1},\vec{x_2})=||\vec{x_1}-\vec{x_2}||_{L_p}=(\sum_{i=1}^n ({x_1}^i-{x_2}^i)^p)^{\frac{1}{p}} $
Riemannian metric: $ D(\vec{x_1},\vec{x_2})=\sqrt{(\vec{x_1}-\vec{x_2})^\top \mathbb{M}(\vec{x_1}-\vec{x_2})} $
where M is a symmetric positive definite $ n\times n $ matrix. Different choices for M enable associating different weights with different components.
In this way, we see that $ \mathbb{R}^n $, $ \mathbb{Z}^n $, $ \mathbb{C}^n $ have many natural metrics, but feature could be in some other set, e.g. a discrete set.
Example of phi with triangle (Figure 1):
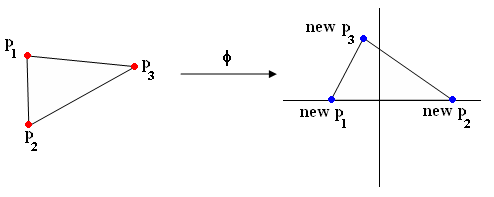
(p1,p2,p3) -> (new p1, new p2, new p3)

