| Line 60: | Line 60: | ||
"Assign category of majority vote of neighbors", where total # of samples = <math>\sum_{i=1}^{d}d_i</math>. | "Assign category of majority vote of neighbors", where total # of samples = <math>\sum_{i=1}^{d}d_i</math>. | ||
| + | |||
| + | Observation: | ||
| + | Training error can be made=0 (by taking V small enough) | ||
| + | but V too small=>spikiness =>high test error | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | **K-nearest neighbor density estimate** | ||
| + | K-Nearest neighbors is a supervised algorithm which basically counts the k-nearest features to determine the class of a sample. The classifiers do not use any model to fit. Given a query, KNN counts the k nearest neighbor points and decide on the class which takes the majority of votes. | ||
| + | It is a simple and efficient algorithm that only calculates the distance of a new sample to the nearest neighbors. | ||
| + | Assign category based on majority vote of k nearest neighbor. The distance can be chosen as Euclidean distance. | ||
| + | |||
| + | .. image:: KNN.jpg | ||
| + | |||
| + | In order to specify the class of green circle, 3-nearest neighbors are counted and because red triangles are more than blue squares, the class of green circle is red triangle. | ||
| + | |||
| + | |||
| + | Assign category based on majority vote of k nearest neighbor | ||
| + | |||
| + | 1) Choose region function <math>\varphi</math> | ||
| + | |||
| + | for example, hypersphere | ||
| + | |||
| + | <math>\varphi \left( \frac{\vec{x}-\vec{x_0}}{h} \right)= 1, \qquad ||\frac{\vec{x}-\vec{x_0}}{h}|| <1 (1)</math> | ||
| + | |||
| + | <math>\quad \quad \qquad =0, \quad else</math> | ||
| + | |||
| + | Dual to this is the K-nearest neighbors in <math>L_2</math> sense (Euclidean distance) | ||
| + | |||
| + | hypercube | ||
| + | |||
| + | <math>\varphi \left( \frac{x-x_0}{h} \right)= 1, \qquad \mid \frac{x-x_0}{h} \mid < \frac{1}{2} (2)</math> | ||
| + | |||
| + | <math>\quad \quad \qquad =0, \quad else</math> (3) | ||
| + | |||
| + | Dual to this is K-nearest neighbor in <math>L_{\infty}</math> sense. Mimi recommended this metric. Why ? .... | ||
| + | |||
| + | If <math>\varphi</math> normal density, there is no dual to this i.e there can not be a metric defined for a gaussian kernel. | ||
| + | |||
| + | 2) Pick K | ||
| + | |||
| + | + k odd, better for 2 category case => no tie vote | ||
| + | + k=1, same as nearest neighbor decision rule | ||
| + | |||
| + | 3) Given <math>x_0 \in</math> feature space and samples <math>\vec{x_1},\cdots, \vec{x_d}</math>, approximate <math>p(x_0)</math> by | ||
| + | |||
| + | <math>\bar{p} (x_0)= \frac{K-1}{dV(x_0)}</math>=> unbiased estimate | ||
| + | |||
| + | where <math>V(x_0)</math> is volume of smallest region R around <math>x_0</math>, containing K samples (called prototypes) | ||
| + | |||
| + | .. image:: ECE662_L16prototypes.jpg | ||
| + | |||
| + | |||
| + | or more generally | ||
| + | |||
| + | <math>\bar{p}(x_0)=\frac{k- # \squad of \squad samples \squad on \squad boundary}{dV(x)}</math> (4) | ||
| + | |||
| + | this yields, | ||
| + | |||
| + | <math>E[\bar{p}(x_0)]=p(x_0)</math> (5) | ||
| + | |||
| + | if <math>p(x_0)</math> where <math>\frac{K}{dV(x_0)}</math> then <math>E[\bar{p}(x_0)]=\frac{K}{K-1}p(\vec{x}_0)</math> | ||
| + | |||
| + | Decision rule is still based majority vote | ||
| + | |||
| + | <math>\frac{K-1}{dV(x_0)} < \frac{K-1}{dV(x)}</math> => yields an unbiased estimate | ||
| + | |||
| + | <math>p(x_0)</math> is a random variable | ||
| + | |||
| + | <math>\bar{p}(x_0)=\frac{K}{dV(x_0)}</math>, where <math>V(x_0)</math> is random variable | ||
| + | |||
| + | => hard to evaluate density of <math>V(x_0)</math> | ||
| + | |||
| + | Consider u | ||
| + | <math>u:=\displaystyle \int_{R - B_R} p(x) dx</math> (6) | ||
| + | |||
| + | where <math>B_R</math> is small band around R | ||
| + | |||
| + | <math>\Rightarrow u \approx p(x_0) V(x_0)</math> (7) | ||
| + | |||
| + | <math>\Delta u = \displaystyle \int _{B_R} p(x) dx</math> (8) | ||
| + | |||
| + | .. image:: ECE662_L16neighbor.jpg | ||
| + | |||
| + | Let G= event "K-1 samples fall into <math>R- B_R</math>" | ||
| + | |||
| + | and H= event "1 samples falls into band" | ||
| + | |||
| + | <math>p(G,H)=p(G)p(H|G)</math> (9) | ||
| + | |||
| + | <math>p(G)=C^{d}_{k-1} u^{k-1} {(1-u)}^{d-k+1}</math> (10) | ||
| + | |||
| + | <math>P(H \mid G)= C^{d-k+1}_{1} \left( \frac{\Delta u}{1-u} \right) { \left( 1- \frac{\Delta u}{1-u} \right) } ^{d-k}</math> (11) | ||
| + | |||
| + | <math>C^{d}_{k+1} \left( \frac{d-k+1}{1} \right) \frac{\Delta u}{1-u} u^{k-1} {(1-u)}^{d-k+1} \left( 1- \frac{\Delta u}{1-u} \right)</math> (12) | ||
| + | |||
| + | |||
| + | keeping the first order term in Taylor approximation | ||
| + | |||
| + | i.e., <math>\left( 1- \frac{\Delta u}{1-u} \right) \approx 1</math> for <math>\Delta u</math> small | ||
| + | |||
| + | <math>\Rightarrow P(G,H) \approx \Delta u \frac{d!}{(k-1)! (d-k)!} u^{k-1} {(1-u)}^{d-k}</math> for <math>\Delta u</math> small | ||
| + | |||
| + | <math>E[ \bar{p} (x_0)]=E \left[ \frac{k-1}{dV(x_0)} \right] \approx E \left[ \frac{(k-1)}{du} p(x_0) \right] = \displaystyle \int \frac{(k-1)}{du} p(x_0) p_u (u) du = p(x_0)</math> (13) | ||
| + | |||
| + | Useful kNN link: | ||
| + | |||
| + | Applet- http://www.cs.cmu.edu/~zhuxj/courseproject/knndemo/KNN.html | ||
Revision as of 13:35, 19 March 2008
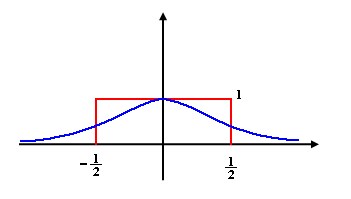
Example of a useful Parzen window function $ \in \mathbb{R}^n $
This function has zero mean, H variance, an n-dimensional density, and is not compactly supported.
You can use any $ \varphi $ such that:
1) $ \varphi(\vec{u})>0,\forall\vec{u} $
2) $ \int_{R^n}\varphi(\vec{u})d\vec{u}=1 $
Given i samples $ \vec{X}_1,\vec{X}_2,...,\vec{X}_i\in{R}^n $,
$ P_i(\vec{X}_0)=\frac{1}{i\cdot{V}_i}\displaystyle\sum_{l=1}^{i} \varphi(\frac{ \vec{X_l}-\vec{X_0} }{h_i} ) $, where $ h_i $ is a number that controls $ V_i $.
i.e. $ V_i=h_i^n $ since $ V_i=\int\varphi(\frac{\vec{u}}{h_i})d\vec{u} $
Letting $ \vec{v}=\frac{\vec{u}}{h_i} $ and $ d\vec{v}=\frac{1}{h_i^n}d\vec{u} $, we have:
$ tex: V_i=\int{h_i^n}\varphi(\vec{v})d\vec{v}=h_i^n\int_{R^n}\varphi(\vec{v})d\vec{v}=h_i^n $
$ p_1(\vec{X}_0)=\frac{1}{i\cdot{h_i^n}}\displaystyle\sum_{l=1}^{i}\varphi(\frac{\vec{X}_l-\vec{X}_0}{h_i}) $ For convergence (in mean square) we need $ i\cdot{V_i}\displaystyle\to\infty $ as $ i\to\infty $
i.e. $ i\cdot{h_i^n}\to\infty $ as $ i\to\infty $, and $ h_i\to{0} $ as $ i\to\infty $.
- PLEASE HELP FIX THE MATLAB CODE !!!!** [Parzen Window Estimation example]
How to make a decision using Parzen window method of density estimation
-> Given samples $ {X_1}^j, {X_2}^j ,..., {X_{d_j}}^j $, for class $ w_j $, i=1,2...,c
The total number of samples for all classes is $ N $.
Choose $ w_j $ such that $ P(w_j|\vec{x_0}) \geq P(w_i|\vec{x_0}) $, for all i=1,2,...,c
$ \Longleftrightarrow p(\vec{x_0}|w_j)P(w_j)\geq p(\vec{x_0}|w_i)P(w_i) \forall i $
$ \Longleftrightarrow p(\vec{x_0}, w_j) \geq p(\vec{x_0}, w_i) \forall i $
,where $ p(\vec{x_0},w_j) \simeq \frac{1}{N\cdot V} \sum_{l=1}^{d_j}\varphi(\frac{\vec{{x_l}^j}-\vec{x_0}}{h}) \geq \frac{1}{N\cdot V} \sum_{l=1}^{d_i}\varphi(\frac{\vec{{x_l}^i}-\vec{x_0}}{h}) $
Therefore, $ \sum_{l=1}^{d_j}\varphi(\frac{\vec{x_l^j}-\vec{x_0}}{h}) \geq \sum_{l=1}^{d_i}\varphi(\frac{\vec{x_l^i}-\vec{x_0}}{h}) $
In the last equation, the first term represents $ K_j $ around $ x_0 $, and the second term represents $ K_i $ around $ x_0 $.
"Assign category of majority vote of neighbors", where total # of samples = $ \sum_{i=1}^{d}d_i $.
Observation: Training error can be made=0 (by taking V small enough) but V too small=>spikiness =>high test error
- K-nearest neighbor density estimate**
K-Nearest neighbors is a supervised algorithm which basically counts the k-nearest features to determine the class of a sample. The classifiers do not use any model to fit. Given a query, KNN counts the k nearest neighbor points and decide on the class which takes the majority of votes. It is a simple and efficient algorithm that only calculates the distance of a new sample to the nearest neighbors. Assign category based on majority vote of k nearest neighbor. The distance can be chosen as Euclidean distance.
.. image:: KNN.jpg
In order to specify the class of green circle, 3-nearest neighbors are counted and because red triangles are more than blue squares, the class of green circle is red triangle.
Assign category based on majority vote of k nearest neighbor
1) Choose region function $ \varphi $
for example, hypersphere
$ \varphi \left( \frac{\vec{x}-\vec{x_0}}{h} \right)= 1, \qquad ||\frac{\vec{x}-\vec{x_0}}{h}|| <1 (1) $
$ \quad \quad \qquad =0, \quad else $
Dual to this is the K-nearest neighbors in $ L_2 $ sense (Euclidean distance)
hypercube
$ \varphi \left( \frac{x-x_0}{h} \right)= 1, \qquad \mid \frac{x-x_0}{h} \mid < \frac{1}{2} (2) $
$ \quad \quad \qquad =0, \quad else $ (3)
Dual to this is K-nearest neighbor in $ L_{\infty} $ sense. Mimi recommended this metric. Why ? ....
If $ \varphi $ normal density, there is no dual to this i.e there can not be a metric defined for a gaussian kernel.
2) Pick K
+ k odd, better for 2 category case => no tie vote + k=1, same as nearest neighbor decision rule
3) Given $ x_0 \in $ feature space and samples $ \vec{x_1},\cdots, \vec{x_d} $, approximate $ p(x_0) $ by
$ \bar{p} (x_0)= \frac{K-1}{dV(x_0)} $=> unbiased estimate
where $ V(x_0) $ is volume of smallest region R around $ x_0 $, containing K samples (called prototypes)
.. image:: ECE662_L16prototypes.jpg
or more generally
$ \bar{p}(x_0)=\frac{k- # \squad of \squad samples \squad on \squad boundary}{dV(x)} $ (4)
this yields,
$ E[\bar{p}(x_0)]=p(x_0) $ (5)
if $ p(x_0) $ where $ \frac{K}{dV(x_0)} $ then $ E[\bar{p}(x_0)]=\frac{K}{K-1}p(\vec{x}_0) $
Decision rule is still based majority vote
$ \frac{K-1}{dV(x_0)} < \frac{K-1}{dV(x)} $ => yields an unbiased estimate
$ p(x_0) $ is a random variable
$ \bar{p}(x_0)=\frac{K}{dV(x_0)} $, where $ V(x_0) $ is random variable
=> hard to evaluate density of $ V(x_0) $
Consider u $ u:=\displaystyle \int_{R - B_R} p(x) dx $ (6)
where $ B_R $ is small band around R
$ \Rightarrow u \approx p(x_0) V(x_0) $ (7)
$ \Delta u = \displaystyle \int _{B_R} p(x) dx $ (8)
.. image:: ECE662_L16neighbor.jpg
Let G= event "K-1 samples fall into $ R- B_R $"
and H= event "1 samples falls into band"
$ p(G,H)=p(G)p(H|G) $ (9)
$ p(G)=C^{d}_{k-1} u^{k-1} {(1-u)}^{d-k+1} $ (10)
$ P(H \mid G)= C^{d-k+1}_{1} \left( \frac{\Delta u}{1-u} \right) { \left( 1- \frac{\Delta u}{1-u} \right) } ^{d-k} $ (11)
$ C^{d}_{k+1} \left( \frac{d-k+1}{1} \right) \frac{\Delta u}{1-u} u^{k-1} {(1-u)}^{d-k+1} \left( 1- \frac{\Delta u}{1-u} \right) $ (12)
keeping the first order term in Taylor approximation
i.e., $ \left( 1- \frac{\Delta u}{1-u} \right) \approx 1 $ for $ \Delta u $ small
$ \Rightarrow P(G,H) \approx \Delta u \frac{d!}{(k-1)! (d-k)!} u^{k-1} {(1-u)}^{d-k} $ for $ \Delta u $ small
$ E[ \bar{p} (x_0)]=E \left[ \frac{k-1}{dV(x_0)} \right] \approx E \left[ \frac{(k-1)}{du} p(x_0) \right] = \displaystyle \int \frac{(k-1)}{du} p(x_0) p_u (u) du = p(x_0) $ (13)
Useful kNN link:
Applet- http://www.cs.cmu.edu/~zhuxj/courseproject/knndemo/KNN.html