| Line 13: | Line 13: | ||
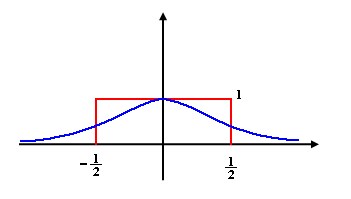
This function has zero mean, H variance, an n-dimensional density, and is not compactly supported. | This function has zero mean, H variance, an n-dimensional density, and is not compactly supported. | ||
| + | |||
| + | You can use any <math>\varphi</math> such that: | ||
| + | |||
| + | 1) <math>\varphi(\vec{u})>0,\forall\vec{u}</math> | ||
| + | |||
| + | 2) <math>\int_{R^n}\varphi(\vec{u})d\vec{u}=1</math> | ||
| + | |||
| + | Given i samples <math>\vec{X}_1,\vec{X}_2,...,\vec{X}_i\in{R}^n</math>, | ||
| + | |||
| + | <math>P_i(\vec{X}_0)=\frac{1}{i\cdot{V}_i}\displaystyle\sum_{l=1}^{i} | ||
| + | \varphi(\frac{ \vec{X_l}-\vec{X_0} }{h_i} )</math>, where <math>h_i</math> is a number that controls <math>V_i</math>. | ||
| + | |||
| + | i.e. <math>V_i=h_i^n</math> since <math>V_i=\int\varphi(\frac{\vec{u}}{h_i})d\vec{u}</math> | ||
| + | |||
| + | Letting <math>\vec{v}=\frac{\vec{u}}{h_i}</math> and <math>d\vec{v}=\frac{1}{h_i^n}d\vec{u}</math>, we have: | ||
| + | |||
| + | .. |Vi_4| image:: tex | ||
| + | :alt: tex: V_i=\int{h_i^n}\varphi(\vec{v})d\vec{v}=h_i^n\int_{R^n}\varphi(\vec{v})d\vec{v}=h_i^n | ||
| + | |||
| + | <math>tex: V_i=\int{h_i^n}\varphi(\vec{v})d\vec{v}=h_i^n\int_{R^n}\varphi(\vec{v})d\vec{v}=h_i^n</math> | ||
| + | |||
| + | <math>p_1(\vec{X}_0)=\frac{1}{i\cdot{h_i^n}}\displaystyle\sum_{l=1}^{i}\varphi(\frac{\vec{X}_l-\vec{X}_0}{h_i})</math> For convergence (in mean square) we need <math>i\cdot{V_i}\displaystyle\to\infty | ||
| + | </math> as <math>i\to\infty</math> | ||
| + | |||
| + | .. |ihi| image:: tex | ||
| + | :alt: tex: i\cdot{h_i^n}\to\infty | ||
| + | |||
| + | .. |hi_inf| image:: tex | ||
| + | :alt: tex: h_i\to{0} | ||
| + | |||
| + | i.e. <math>i\cdot{h_i^n}\to\infty</math> as <math>i\to\infty</math>, and <math>h_i\to{0}</math> as <math>i\to\infty</math>. | ||
| + | |||
| + | **PLEASE HELP FIX THE MATLAB CODE !!!!** [Parzen Window Estimation example] | ||
| + | |||
| + | |||
| + | How to make a decision using Parzen window method of density estimation | ||
| + | |||
| + | -> Given samples <math>X_1^j, X_2^j ,..., X_d_j^j</math>, for class <math>w_j</math>, i=1,2...,c | ||
| + | |||
| + | Choose <math>w_j</math> such that, <math>P(w_j|\vec{x_o}) \geq P(w_i|\vec{x_o})</math>, for all i=1,2,...,c | ||
| + | |||
| + | <math>\Longleftrightarrow p(\vec{x_o}|w_j)P(w_j) \geq p(\vec{x_o}|w_i})P(w_i) \forall i</math> | ||
| + | |||
| + | <math>\Longleftrightarrow p(\vec{x_o}, w_j) \geq p(\vec{x_o}, w_i}) \forall i</math> | ||
| + | |||
| + | ,where <math>p(\vec{x_o},w_j) \simeq \frac{1}{total # of samples \mul x V} \sum_{l=1}^{d_j}\varphi(\frac{\vec{x_l^j}-\vec{x_0}}{h}) \geq \frac{1}{total # of samples x V} \sum_{l=1}^{d_i}\varphi(\frac{\vec{x_l^i}-\vec{x_0}}{h})</math> | ||
| + | |||
| + | Therefore, <math>\sum_{l=1}^{d_j}\varphi(\frac{\vec{x_l^j}-\vec{x_0}}{h}) \geq \sum_{l=1}^{d_i}\varphi(\frac{\vec{x_l^i}-\vec{x_0}}{h})</math> | ||
| + | |||
| + | In the last equation, the first term represents <math>K_j</math> around <math>x_o</math>, and the second term represents <math>K_i</math> around <math>x_o</math>. | ||
| + | |||
| + | "Assign category of majority vote of neighbors", where total # of samples = <math>\sum_{i=1}^{d}d_i</math>. | ||
Revision as of 12:58, 19 March 2008
Example of a useful Parzen window function $ \in \mathbb{R}^n $
This function has zero mean, H variance, an n-dimensional density, and is not compactly supported.
You can use any $ \varphi $ such that:
1) $ \varphi(\vec{u})>0,\forall\vec{u} $
2) $ \int_{R^n}\varphi(\vec{u})d\vec{u}=1 $
Given i samples $ \vec{X}_1,\vec{X}_2,...,\vec{X}_i\in{R}^n $,
$ P_i(\vec{X}_0)=\frac{1}{i\cdot{V}_i}\displaystyle\sum_{l=1}^{i} \varphi(\frac{ \vec{X_l}-\vec{X_0} }{h_i} ) $, where $ h_i $ is a number that controls $ V_i $.
i.e. $ V_i=h_i^n $ since $ V_i=\int\varphi(\frac{\vec{u}}{h_i})d\vec{u} $
Letting $ \vec{v}=\frac{\vec{u}}{h_i} $ and $ d\vec{v}=\frac{1}{h_i^n}d\vec{u} $, we have:
.. |Vi_4| image:: tex
- alt: tex: V_i=\int{h_i^n}\varphi(\vec{v})d\vec{v}=h_i^n\int_{R^n}\varphi(\vec{v})d\vec{v}=h_i^n
$ tex: V_i=\int{h_i^n}\varphi(\vec{v})d\vec{v}=h_i^n\int_{R^n}\varphi(\vec{v})d\vec{v}=h_i^n $
$ p_1(\vec{X}_0)=\frac{1}{i\cdot{h_i^n}}\displaystyle\sum_{l=1}^{i}\varphi(\frac{\vec{X}_l-\vec{X}_0}{h_i}) $ For convergence (in mean square) we need $ i\cdot{V_i}\displaystyle\to\infty $ as $ i\to\infty $
.. |ihi| image:: tex
- alt: tex: i\cdot{h_i^n}\to\infty
.. |hi_inf| image:: tex
- alt: tex: h_i\to{0}
i.e. $ i\cdot{h_i^n}\to\infty $ as $ i\to\infty $, and $ h_i\to{0} $ as $ i\to\infty $.
- PLEASE HELP FIX THE MATLAB CODE !!!!** [Parzen Window Estimation example]
How to make a decision using Parzen window method of density estimation
-> Given samples $ X_1^j, X_2^j ,..., X_d_j^j $, for class $ w_j $, i=1,2...,c
Choose $ w_j $ such that, $ P(w_j|\vec{x_o}) \geq P(w_i|\vec{x_o}) $, for all i=1,2,...,c
$ \Longleftrightarrow p(\vec{x_o}|w_j)P(w_j) \geq p(\vec{x_o}|w_i})P(w_i) \forall i $
$ \Longleftrightarrow p(\vec{x_o}, w_j) \geq p(\vec{x_o}, w_i}) \forall i $
,where $ p(\vec{x_o},w_j) \simeq \frac{1}{total # of samples \mul x V} \sum_{l=1}^{d_j}\varphi(\frac{\vec{x_l^j}-\vec{x_0}}{h}) \geq \frac{1}{total # of samples x V} \sum_{l=1}^{d_i}\varphi(\frac{\vec{x_l^i}-\vec{x_0}}{h}) $
Therefore, $ \sum_{l=1}^{d_j}\varphi(\frac{\vec{x_l^j}-\vec{x_0}}{h}) \geq \sum_{l=1}^{d_i}\varphi(\frac{\vec{x_l^i}-\vec{x_0}}{h}) $
In the last equation, the first term represents $ K_j $ around $ x_o $, and the second term represents $ K_i $ around $ x_o $.
"Assign category of majority vote of neighbors", where total # of samples = $ \sum_{i=1}^{d}d_i $.