| Line 14: | Line 14: | ||
**Step 1:** Choose "shape" of your window by introducing a "window function" | **Step 1:** Choose "shape" of your window by introducing a "window function" | ||
| − | + | ||
| + | e.g. if <math>R_i</math> is hybercube in <math>\mathbb{R}^n</math> with side-length <math>h_i</math>, then the window function is <math>\varphi</math>. | ||
<math>\varphi(\vec{u})=\varphi(u_1, u_2, \ldots, u_n)=1</math> if <math>|u_i|<\frac{1}{2}, \forall i</math> otherwise 0. | <math>\varphi(\vec{u})=\varphi(u_1, u_2, \ldots, u_n)=1</math> if <math>|u_i|<\frac{1}{2}, \forall i</math> otherwise 0. | ||
| Line 26: | Line 27: | ||
[[Image:Lec15_square3D_OldKiwi.jpg]] | [[Image:Lec15_square3D_OldKiwi.jpg]] | ||
| + | Given the shape for parzen window by <math>\varphi</math>, we can scale and shift it as required by the method. | ||
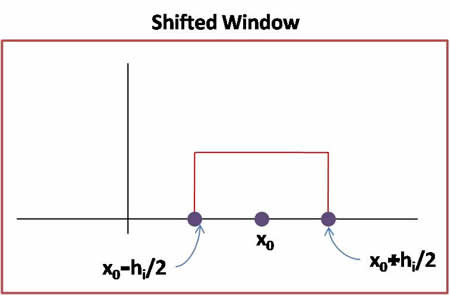
| + | <math>\varphi(\frac{\vec{x}-\vec{x_0}}{h_i})</math> is window centered at <math>\vec{x_0}</math> scaled by a factor <math>h_i</math>, i.e. its side-length is <math>h_i</math>. | ||
| − | . | + | [[Image:Lec15_shiftWindow_OldKiwi.jpg]] |
| − | + | ||
| − | + | **Step 2:** Write the density estimate of <math>p(\vec{x})</math> at <math>\vec{x_0} \in R_i</math> using window function, denoted by <math>p_i(\vec{x_0})</math>. | |
| − | + | ||
| − | + | We have number of samples for <math>\{\vec{x_1}, \vec{x_2}, \ldots, \vec{x_i}\}</math> inside <math>R_i</math> denoted by <math>K_i</math> | |
| − | + | <math>\sum_{l=1}^{i}\varphi(\frac{\vec{x_l}-\vec{x_0}}{h_i})</math> | |
| − | + | So, <math>p_i(\vec{x_0})=\frac{k_i}{iV_i}=\frac{1}{iV_i}\sum_{l=1}^{i}\varphi(\frac{\vec{x_l}-\vec{x_0}}{h_i})</math> | |
| − | + | Let <math>\delta_i(\vec{u})=\frac{1}{V_i}\varphi(\frac{\vec{u}}{h_i})</math> | |
| − | + | ||
| − | + | <math>p_i(\vec{x_0})=\frac{1}{i}\sum_{l=1}^{i}\delta_i(\vec{x_l}-\vec{x_0})</math> | |
| − | + | ||
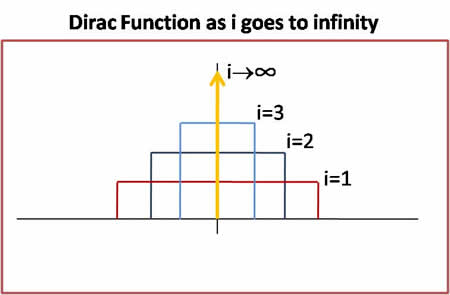
| − | + | This last equation is an average over impulses. For any l, <math>\lim_{h_i->0}\delta(\vec{x_l}-\vec{x_0})</math> is [Dirac delta Function]. We do not want to average over dirac delta functions. Our objective is that <math>p_i(\vec{x_0})</math> should converge to true value <math>p(\vec{x})</math>, as <math>i\rightarrow \infty</math> | |
| − | + | [[Image:Lec15_dirac_OldKiwi.jpg]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
.. |MSS1| image:: tex | .. |MSS1| image:: tex | ||
| − | + | :alt: tex: \lim_{i\rightarrow \infty}E\{p_i(\vec{x_0})\}=p(\vec{x_0}) | |
.. |MSS2| image:: tex | .. |MSS2| image:: tex | ||
| − | + | :alt: tex: \lim_{i\rightarrow \infty}Var\{p_i(\vec{x_0})\}=0 | |
.. |MSS3| image:: tex | .. |MSS3| image:: tex | ||
| − | + | :alt: tex: p_i(\vec{x_0}) \longrightarrow p(\vec{x_0}) | |
| − | + | ||
| − | + | ||
| − | + | ||
**What does convergence mean here?** | **What does convergence mean here?** | ||
| − | Observe | + | Observe <math>\{p_i(\vec{x_0})\}</math> is a sequence of random variables since <math>p_i(\vec{x_0})</math> depends on random variables |sample_space_i|. |
What do we mean by convergence of a sequence of random variables (There are many definitions). We pick "Convergence in mean square" sense, i.e. | What do we mean by convergence of a sequence of random variables (There are many definitions). We pick "Convergence in mean square" sense, i.e. | ||
| Line 113: | Line 71: | ||
.. |kkh01| image:: tex | .. |kkh01| image:: tex | ||
| − | + | :alt: tex: E(p_i(\vec{x_o})) | |
.. |kkh02| image:: tex | .. |kkh02| image:: tex | ||
| − | + | :alt: tex: p(\vec{x_o}) | |
.. |kkh03| image:: tex | .. |kkh03| image:: tex | ||
| − | + | :alt: tex: i\to\infty | |
.. |kkh04| image:: tex | .. |kkh04| image:: tex | ||
| − | + | :alt: tex: h_i \to\infty | |
.. |kkh05| image:: tex | .. |kkh05| image:: tex | ||
| − | + | :alt: tex: V_i\to\infty | |
.. |kkh06| image:: tex | .. |kkh06| image:: tex | ||
| − | + | ..alt: tex: Var(p_i\vec{x_o}) | |
| Line 135: | Line 93: | ||
.. |jinha_pix0| image:: tex | .. |jinha_pix0| image:: tex | ||
| − | + | :alt: tex: \displaystyle p_i (x_0) = \frac{1}{i} \sum_{l=1}^{i} \delta_i (\vec{x}_l - \vec{x}_0) | |
|jinha_epix0| | |jinha_epix0| | ||
.. |jinha_epix0| image:: tex | .. |jinha_epix0| image:: tex | ||
| − | + | :alt: tex: \displaystyle E[p_i(x_0)] = \frac{1}{i} \sum_{l=1}^{i} E[ \delta_i (\vec{x}_l - \vec{x}_0) ] = \frac{1}{i} \sum_{l=1}^{i} \int \delta_i (\vec{x}_l - \vec{x}_0) p(\vec{x}_l) dx_l \rightarrow p(\vec{x}_0) | |
| Line 151: | Line 109: | ||
.. |jinha_varpix0| image:: tex | .. |jinha_varpix0| image:: tex | ||
| − | + | :alt: tex: Var(p_i(x_0)) \rightarrow 0 | |
|jinha_varpix0_1| | |jinha_varpix0_1| | ||
.. |jinha_varpix0_1| image:: tex | .. |jinha_varpix0_1| image:: tex | ||
| − | + | :alt: tex: \displaystyle Var(p_i(x_0)) = Var(\sum_{l=1}^{i} \frac{1}{i} \delta_i(\vec{x}_l - \vec{x}_0)) = \sum_{l=1}^{i} Var(\frac{1}{i} \delta_i(\vec{x}_l - \vec{x}_0)) | |
|jinha_varpix0_2| | |jinha_varpix0_2| | ||
.. |jinha_varpix0_2| image:: tex | .. |jinha_varpix0_2| image:: tex | ||
| − | + | :alt: tex: \displaystyle = \sum_{l=1}^{i} E \left[ \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} - E\left[ \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right] \right)^2 \right] = \sum_{l=1}^{i} E \left[ \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right)^2 \right] - \left( E\left[ \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right] \right)^2 | |
| − | + | ||
We know that second term is non-negative, therefore we can write | We know that second term is non-negative, therefore we can write | ||
| Line 168: | Line 126: | ||
.. |jinha_varpix0_3| image:: tex | .. |jinha_varpix0_3| image:: tex | ||
| − | + | :alt: tex: \displaystyle Var(p_i(x_0)) \le \sum_{l=1}^{i} E \left[ \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right)^2 \right] | |
|jinha_varpix0_4| | |jinha_varpix0_4| | ||
.. |jinha_varpix0_4| image:: tex | .. |jinha_varpix0_4| image:: tex | ||
| − | + | :alt: tex: \displaystyle \rightarrow Var(p_i(x_0)) \le \sum_{l=1}^{i} \int \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right)^2 p(x_l) dx_l | |
|jinha_varpix0_5| | |jinha_varpix0_5| | ||
.. |jinha_varpix0_5| image:: tex | .. |jinha_varpix0_5| image:: tex | ||
| − | + | :alt: tex: \displaystyle \rightarrow Var(p_i(x_0)) \le \sum_{l=1}^{i} \frac{1}{i^2} \int \frac{\psi \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i}\right)}{V_i} \frac{\psi \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i}\right)}{V_i} p(x_l) dx_l | |
|jinha_varpix0_6| | |jinha_varpix0_6| | ||
.. |jinha_varpix0_6| image:: tex | .. |jinha_varpix0_6| image:: tex | ||
| − | + | :alt: tex: \displaystyle \rightarrow Var(p_i(x_0)) \le \frac{1}{i V_i} sup\psi \int \sum_{l=1}^{i} \delta_i (x_l - x_0) p(x_l) dx_l | |
|jinha_varpix0_7| | |jinha_varpix0_7| | ||
.. |jinha_varpix0_7| image:: tex | .. |jinha_varpix0_7| image:: tex | ||
| − | + | :alt: tex: \displaystyle \therefore Var(p_i(x_0)) \le \frac{1}{i V_i} sup\psi E [p_i(x_0)] | |
| Line 200: | Line 158: | ||
.. |a_1| image:: tex | .. |a_1| image:: tex | ||
| − | + | :alt: tex: v_i | |
.. |a_2| image:: tex | .. |a_2| image:: tex | ||
| − | + | :alt: tex: var(P_i (\vec{x_0})) | |
.. |a_3| image:: tex | .. |a_3| image:: tex | ||
| − | + | :alt: tex: i V_i \rightarrow \infty | |
.. |a_4| image:: tex | .. |a_4| image:: tex | ||
| − | + | :alt: tex: i \rightarrow \infty | |
.. |a_5| image:: tex | .. |a_5| image:: tex | ||
| − | + | :alt: tex: v_i= \frac{1}{\sqrt i}, v_i=\frac{13}{\sqrt i} or \frac{17}{\sqrt i} | |
.. |a_6| image:: tex | .. |a_6| image:: tex | ||
| − | + | :alt: tex: var(P_i (\vec{x_0})) \rightarrow 0, as i \rightarrow \infty | |
Revision as of 15:18, 20 March 2008
Figure 1
Figure 2
Parzen Window Method
- Step 1:** Choose "shape" of your window by introducing a "window function"
e.g. if $ R_i $ is hybercube in $ \mathbb{R}^n $ with side-length $ h_i $, then the window function is $ \varphi $.
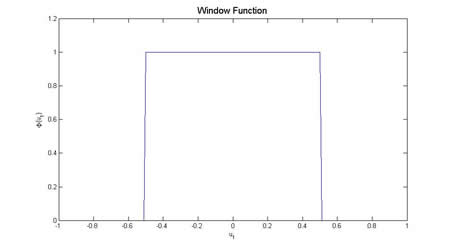
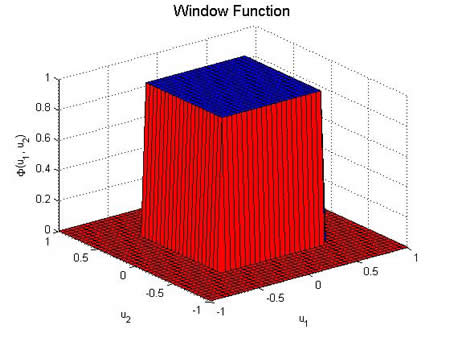
$ \varphi(\vec{u})=\varphi(u_1, u_2, \ldots, u_n)=1 $ if $ |u_i|<\frac{1}{2}, \forall i $ otherwise 0.
Examples of Parzen windows
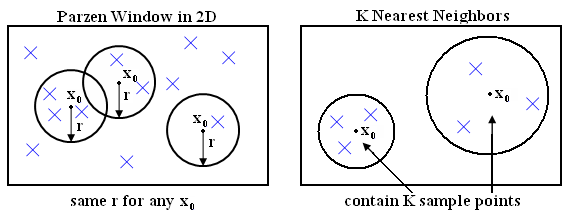
Given the shape for parzen window by $ \varphi $, we can scale and shift it as required by the method.
$ \varphi(\frac{\vec{x}-\vec{x_0}}{h_i}) $ is window centered at $ \vec{x_0} $ scaled by a factor $ h_i $, i.e. its side-length is $ h_i $.
- Step 2:** Write the density estimate of $ p(\vec{x}) $ at $ \vec{x_0} \in R_i $ using window function, denoted by $ p_i(\vec{x_0}) $.
We have number of samples for $ \{\vec{x_1}, \vec{x_2}, \ldots, \vec{x_i}\} $ inside $ R_i $ denoted by $ K_i $
$ \sum_{l=1}^{i}\varphi(\frac{\vec{x_l}-\vec{x_0}}{h_i}) $
So, $ p_i(\vec{x_0})=\frac{k_i}{iV_i}=\frac{1}{iV_i}\sum_{l=1}^{i}\varphi(\frac{\vec{x_l}-\vec{x_0}}{h_i}) $
Let $ \delta_i(\vec{u})=\frac{1}{V_i}\varphi(\frac{\vec{u}}{h_i}) $
$ p_i(\vec{x_0})=\frac{1}{i}\sum_{l=1}^{i}\delta_i(\vec{x_l}-\vec{x_0}) $
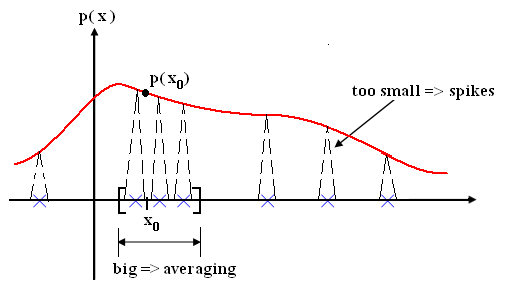
This last equation is an average over impulses. For any l, $ \lim_{h_i->0}\delta(\vec{x_l}-\vec{x_0}) $ is [Dirac delta Function]. We do not want to average over dirac delta functions. Our objective is that $ p_i(\vec{x_0}) $ should converge to true value $ p(\vec{x}) $, as $ i\rightarrow \infty $
.. |MSS1| image:: tex
- alt: tex: \lim_{i\rightarrow \infty}E\{p_i(\vec{x_0})\}=p(\vec{x_0})
.. |MSS2| image:: tex
- alt: tex: \lim_{i\rightarrow \infty}Var\{p_i(\vec{x_0})\}=0
.. |MSS3| image:: tex
- alt: tex: p_i(\vec{x_0}) \longrightarrow p(\vec{x_0})
- What does convergence mean here?**
Observe $ \{p_i(\vec{x_0})\} $ is a sequence of random variables since $ p_i(\vec{x_0}) $ depends on random variables |sample_space_i|. What do we mean by convergence of a sequence of random variables (There are many definitions). We pick "Convergence in mean square" sense, i.e.
If |MSS1|
and |MSS2|
then we say |MSS3| in mean square as |i_tends_infty|
.. |kkh01| image:: tex
- alt: tex: E(p_i(\vec{x_o}))
.. |kkh02| image:: tex
- alt: tex: p(\vec{x_o})
.. |kkh03| image:: tex
- alt: tex: i\to\infty
.. |kkh04| image:: tex
- alt: tex: h_i \to\infty
.. |kkh05| image:: tex
- alt: tex: V_i\to\infty
.. |kkh06| image:: tex ..alt: tex: Var(p_i\vec{x_o})
- First condition:**
From the previous result, |jinha_pix0|
.. |jinha_pix0| image:: tex
- alt: tex: \displaystyle p_i (x_0) = \frac{1}{i} \sum_{l=1}^{i} \delta_i (\vec{x}_l - \vec{x}_0)
|jinha_epix0|
.. |jinha_epix0| image:: tex
- alt: tex: \displaystyle E[p_i(x_0)] = \frac{1}{i} \sum_{l=1}^{i} E[ \delta_i (\vec{x}_l - \vec{x}_0) ] = \frac{1}{i} \sum_{l=1}^{i} \int \delta_i (\vec{x}_l - \vec{x}_0) p(\vec{x}_l) dx_l \rightarrow p(\vec{x}_0)
We don't need an infinity number of samples to make |kkh01| converge to |kkh02| as |kkh03|.
We just need |kkh04| (iie. |kkh05|)
- To make it sure** |jinha_varpix0|, what should we do?
.. |jinha_varpix0| image:: tex
- alt: tex: Var(p_i(x_0)) \rightarrow 0
|jinha_varpix0_1|
.. |jinha_varpix0_1| image:: tex
- alt: tex: \displaystyle Var(p_i(x_0)) = Var(\sum_{l=1}^{i} \frac{1}{i} \delta_i(\vec{x}_l - \vec{x}_0)) = \sum_{l=1}^{i} Var(\frac{1}{i} \delta_i(\vec{x}_l - \vec{x}_0))
|jinha_varpix0_2|
.. |jinha_varpix0_2| image:: tex
- alt: tex: \displaystyle = \sum_{l=1}^{i} E \left[ \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} - E\left[ \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right] \right)^2 \right] = \sum_{l=1}^{i} E \left[ \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right)^2 \right] - \left( E\left[ \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right] \right)^2
We know that second term is non-negative, therefore we can write
|jinha_varpix0_3|
.. |jinha_varpix0_3| image:: tex
- alt: tex: \displaystyle Var(p_i(x_0)) \le \sum_{l=1}^{i} E \left[ \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right)^2 \right]
|jinha_varpix0_4|
.. |jinha_varpix0_4| image:: tex
- alt: tex: \displaystyle \rightarrow Var(p_i(x_0)) \le \sum_{l=1}^{i} \int \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right)^2 p(x_l) dx_l
|jinha_varpix0_5|
.. |jinha_varpix0_5| image:: tex
- alt: tex: \displaystyle \rightarrow Var(p_i(x_0)) \le \sum_{l=1}^{i} \frac{1}{i^2} \int \frac{\psi \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i}\right)}{V_i} \frac{\psi \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i}\right)}{V_i} p(x_l) dx_l
|jinha_varpix0_6|
.. |jinha_varpix0_6| image:: tex
- alt: tex: \displaystyle \rightarrow Var(p_i(x_0)) \le \frac{1}{i V_i} sup\psi \int \sum_{l=1}^{i} \delta_i (x_l - x_0) p(x_l) dx_l
|jinha_varpix0_7|
.. |jinha_varpix0_7| image:: tex
- alt: tex: \displaystyle \therefore Var(p_i(x_0)) \le \frac{1}{i V_i} sup\psi E [p_i(x_0)]
If fixed i=d, then as |a_1| increased, |a_2| decreased.
But, if |a_3| , as |a_4|
(for example, if |a_5|)
then, |a_6|
.. |a_1| image:: tex
- alt: tex: v_i
.. |a_2| image:: tex
- alt: tex: var(P_i (\vec{x_0}))
.. |a_3| image:: tex
- alt: tex: i V_i \rightarrow \infty
.. |a_4| image:: tex
- alt: tex: i \rightarrow \infty
.. |a_5| image:: tex
- alt: tex: v_i= \frac{1}{\sqrt i}, v_i=\frac{13}{\sqrt i} or \frac{17}{\sqrt i}
.. |a_6| image:: tex
- alt: tex: var(P_i (\vec{x_0})) \rightarrow 0, as i \rightarrow \infty
Here are some useful links to "Parzen-window Density Estimation"
http://www.cs.utah.edu/~suyash/Dissertation_html/node11.html
http://en.wikipedia.org/wiki/Parzen_window
http://www.personal.rdg.ac.uk/~sis01xh/teaching/CY2D2/Pattern2.pdf
http://www.eee.metu.edu.tr/~alatan/Courses/Demo/AppletParzen.html