(→Support Vector Machines) |
(→==) |
||
| Line 131: | Line 131: | ||
Proposed by Aizerman in another context used by Vapnik,Boser, Guyon to upgrade [SVM] to find non-linear decision boundary based on observation that [SVM] training only introduces |khh5| | Proposed by Aizerman in another context used by Vapnik,Boser, Guyon to upgrade [SVM] to find non-linear decision boundary based on observation that [SVM] training only introduces |khh5| | ||
| − | + | |khh13| | |
.. |khh13| image:: tex | .. |khh13| image:: tex | ||
| − | + | :alt: tex: y_i \cdot y_j = \varphi (x_i) \cdot \varphi (x_j) | |
A kernel function |khh14| for a given mapping |khh15| is a function such that |khh16|. | A kernel function |khh14| for a given mapping |khh15| is a function such that |khh16|. | ||
.. |khh14| image:: tex | .. |khh14| image:: tex | ||
| − | + | :alt: tex: K:\Re ^k \times \Re ^k \rightarrow \Re | |
.. |khh15| image:: tex | .. |khh15| image:: tex | ||
| − | + | :alt: tex: \varphi | |
.. |khh16| image:: tex | .. |khh16| image:: tex | ||
| − | + | :alt: tex: K(x,x')=\varphi (x) \cdot \varphi (x') | |
Therefore, |khh17| -> No need to compute |khh18| and no need to know |khh15| | Therefore, |khh17| -> No need to compute |khh18| and no need to know |khh15| | ||
.. |khh17| image:: tex | .. |khh17| image:: tex | ||
| − | + | :alt: tex: y_i \cdot y_j = K(x_i,x_j) | |
.. |khh18| image:: tex | .. |khh18| image:: tex | ||
| − | + | :alt: tex: \varphi (x_i), \varphi (x_j) | |
| − | In order to exploit kernel trick, we need to have good kernel functions. One way to do that is to choose |fx| (called basis functions) and use it to find corresponding kernel. Another method is to construct kernel functions directly by making sure that the function is a valid kernel which means it corresponds to a scalar product in some feature space. | + | In order to exploit kernel trick, we need to have good kernel functions. One way to do that is to choose |fx| (called basis functions) and use it to find corresponding kernel. Another method is to construct kernel functions directly by making sure that the function is a valid kernel which means it corresponds to a scalar product in some feature space. |
Necessary and sufficient condition for a function to be a valid kernel is Gram Matrix K whose elements are |kxx| to be positive semidefinite. Here are some figures to show the general characteristics of a kernel function. | Necessary and sufficient condition for a function to be a valid kernel is Gram Matrix K whose elements are |kxx| to be positive semidefinite. Here are some figures to show the general characteristics of a kernel function. | ||
.. |fx| image:: tex | .. |fx| image:: tex | ||
| − | + | :alt: tex: \varphi (x) | |
.. |kxx| image:: tex | .. |kxx| image:: tex | ||
| − | + | :alt: tex: k(x_n, x_m) | |
.. image:: kernel.jpg | .. image:: kernel.jpg | ||
| Line 169: | Line 169: | ||
The left hand side figure represents the set of basis functions, and the right hand side represents the Gaussian Kernel Function. | The left hand side figure represents the set of basis functions, and the right hand side represents the Gaussian Kernel Function. | ||
| − | A powerful method for creating good kernel functions is to use simpler kernel functions to build new ones. Because, we can manipulate kernel functions by using some transformations such as scalar multiplications, summing two kernel functions, inserting kernel functions to some other functions and so on. | + | A powerful method for creating good kernel functions is to use simpler kernel functions to build new ones. Because, we can manipulate kernel functions by using some transformations such as scalar multiplications, summing two kernel functions, inserting kernel functions to some other functions and so on. |
2 Nice examples can be found in [Support Vector Machines : 1-D Example] and [SVM: 2-D Example] | 2 Nice examples can be found in [Support Vector Machines : 1-D Example] and [SVM: 2-D Example] | ||
| Line 185: | Line 185: | ||
Note : K is kernel for other functions |L13_4| | Note : K is kernel for other functions |L13_4| | ||
| − | (for example |L13_5| | + | (for example |L13_5| |
one-to-one correspondence between kernel and mapping |L13_4| s | one-to-one correspondence between kernel and mapping |L13_4| s | ||
.. |L13_1| image:: tex | .. |L13_1| image:: tex | ||
| − | + | :alt: tex: \varphi (x_1 , x_2)=(x_1^2,\sqrt{2} x_1 x_2, x_2^2 ) | |
.. |L13_2| image:: tex | .. |L13_2| image:: tex | ||
| − | + | :alt: tex: \varphi (x_1 , x_2) \varphi (\acute{x_1} , \acute{x_2})=x_1^2 \acute{x_1^2}+2x_1 x_2 \acute{x_1} \acute{x_2} + x_2^2 \acute{x_2^2} | |
.. |L13_2_2| image:: tex | .. |L13_2_2| image:: tex | ||
| − | + | :alt: tex: (x_1^2 \acute{x_1^2} + x_2^2 \acute{x_2^2} )^2 = [(x_1, x_2) (\acute{x_1^2}, \acute{x_2^2})]^2 | |
.. |L13_3| image:: tex | .. |L13_3| image:: tex | ||
| − | + | :alt: tex: K(\vec x, \acute{\vec x} ) = (\vec x, \acute{\vec x} )^2 | |
.. |L13_4| image:: tex | .. |L13_4| image:: tex | ||
| − | + | :alt: tex: \varphi | |
.. |L13_5| image:: tex | .. |L13_5| image:: tex | ||
| − | + | :alt: tex: \varphi (x_1 , x_2) = \frac {1}{\sqrt{2}} (x_1^2 - x_2^2, 2x_1^2 x_2^2, x_1^2 + x_2^2) | |
| + | |||
| + | == Lectures == | ||
| + | [http://balthier.ecn.purdue.edu/index.php/Lecture_1_-_Introduction 1] [http://balthier.ecn.purdue.edu/index.php/Lecture_2_-_Decision_Hypersurfaces 2] [http://balthier.ecn.purdue.edu/index.php/Lecture_3_-_Bayes_classification 3] | ||
| + | [http://balthier.ecn.purdue.edu/index.php/Lecture_4_-_Bayes_Classification 4] [http://balthier.ecn.purdue.edu/index.php/Lecture_5_-_Discriminant_Functions 5] [http://balthier.ecn.purdue.edu/index.php/Lecture_6_-_Discriminant_Functions 6] [http://balthier.ecn.purdue.edu/index.php/Lecture_7_-_MLE_and_BPE 7] [http://balthier.ecn.purdue.edu/index.php/Lecture_8_-_MLE%2C_BPE_and_Linear_Discriminant_Functions 8] [http://balthier.ecn.purdue.edu/index.php/Lecture_9_-_Linear_Discriminant_Functions 9] [http://balthier.ecn.purdue.edu/index.php/Lecture_10_-_Batch_Perceptron_and_Fisher_Linear_Discriminant 10] [http://balthier.ecn.purdue.edu/index.php/Lecture_11_-_Fischer%27s_Linear_Discriminant_again 11] [http://balthier.ecn.purdue.edu/index.php/Lecture_12_-_Support_Vector_Machine_and_Quadratic_Optimization_Problem 12] [http://balthier.ecn.purdue.edu/index.php/Lecture_13_-_Kernel_function_for_SVMs_and_ANNs_introduction 13] [http://balthier.ecn.purdue.edu/index.php/Lecture_14_-_ANNs%2C_Non-parametric_Density_Estimation_%28Parzen_Window%29 14] [http://balthier.ecn.purdue.edu/index.php/Lecture_15_-_Parzen_Window_Method 15] [http://balthier.ecn.purdue.edu/index.php/Lecture_16_-_Parzen_Window_Method_and_K-nearest_Neighbor_Density_Estimate 16] [http://balthier.ecn.purdue.edu/index.php/Lecture_17_-_Nearest_Neighbors_Clarification_Rule_and_Metrics 17] [http://balthier.ecn.purdue.edu/index.php/Lecture_18_-_Nearest_Neighbors_Clarification_Rule_and_Metrics%28Continued%29 18] | ||
Revision as of 09:59, 20 March 2008
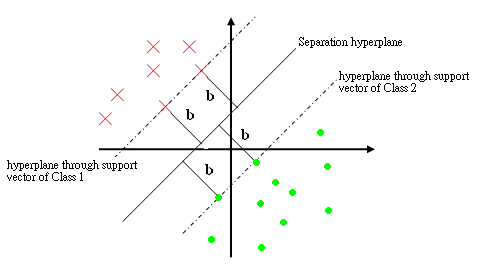
Support Vector Machines
(Continued from Lecture 11)
- Definition
The support vectors are the training points $ y_i $ such that $ \vec{c}\cdot{y_i}=b,\forall{i} $. i.e. they are the closest to the hyperplane.
- How to Train a Support Vector Machine (SVM)
We want to find a $ \vec{c} $ such that $ \vec{c}\cdot{y_i} \geq b, \forall{i} $. This however, is wishful thinking, so we try to find this for as many training samples as possible with $ b $ as large as possible.
Observe: If $ \vec{c} $ is a solution with margin $ b $, then $ \alpha\vec{c} $ is a solution with margin $ \alpha b, \forall{\alpha} \in \Re > 0 $
So to pose the problem well, we demand that $ \vec{c}\cdot{y_i} \geq 1, '\forall{i}' $ and try to minimize $ \vec{c} $
For small training sets, we can use a training method similar to online [perceptron]
1) Pick a plane |c_vector| 2) Find the worst classified sample. |yi_0| (Note: This step is computationally expensive for large data sets) 3) Move plane |c_vector| to improve the classification 4) Repeat steps 2-3 until the algorithm converges
.. |norm_c| image:: tex
:alt: tex: ||\vec{c}||
.. |c_dot_yi_3| image:: tex
:alt: tex: \vec{c}\cdot{y_i}=1,\forall{i}
.. |half_norm_c_sq| image:: tex
:alt: tex: \frac{1}{2}||\vec{c}||^2
We want to minimize |norm_c| subject to the constraints |c_dot_yi_3| (i.e. correct classification). Note: Optimizing |norm_c| is hard, because the function is not convex. Instead, optimize |half_norm_c_sq| (convex function with the same optimum).
.. |c_yi_X| image:: tex
:alt: tex: \vec{c}\cdot{y}_i\ge1,\forall{i}
.. |c_yi_SV| image:: tex
:alt: tex: \vec{c}\cdot{y}_i=1,\forall
.. |yi| image:: tex
:alt: tex: y_i
This gives a [Quadratic Optimization Problem]: Minimize |half_norm_c_sq| subject to the constraints |c_yi_X|. However, we should demand that |c_yi_SV| support vectors |yi|.
Formulate using [Lagrange multipliers]: (Someone should continue the notes from this point)
Karush-Kuhn-Tucker Construction
==========
Reformulate as "Dual Problem"
Maximize |khh1|, where i, j are indices of SV.
under constraint |khh2|, and |khh3|
.. |khh1| image:: tex
:alt: tex: L(\alpha)=\displaystyle \sum_{i} \alpha_{i}-\frac{1}{2}\sum_{i,j} \alpha _i \alpha_j y_i \cdot y_j
.. |khh2| image:: tex
:alt: tex: \displaystyle \sum_{i=1}^{d_1}\alpha _i - \sum_{i=d+1}^{d} \alpha _i = 0
.. |khh3| image:: tex
:alt: tex: \alpha_i \geq 0, \quad \forall{i}
then find |khh4|.
.. |khh4| image:: tex
:alt: tex: \vec{c}=\sum_{i} \alpha_{i} y_i
Key points
+ L only depends on SV + L only depends on |khh5|, not |khh6| or |khh7| explicitly
.. |khh5| image:: tex
:alt: tex: y_{i} \cdot y_{j}
.. |khh6| image:: tex
:alt: tex: y_i
.. |khh7| image:: tex
:alt: tex: y_j
Recall: maximize |khh8|
.. |khh8| image:: tex
:alt: tex: L(c,\vec{\alpha})=\frac{1}{2}||\vec{c}||^2 - \displaystyle \sum_{i} \alpha _i (\vec{c} \cdot y_i -1 )
When data is not linearly separable, max |khh9|, Do not try this numerial optimization.
.. |khh9| image:: tex
:alt: tex: L(c,\vec{\alpha})=\infty
+ How to train a support vector machine using nonlinearly separable data. Define "soft margins" by introducing "slack variable" |khh9| , which measure misclassification of |khh6|.
.. |khh9| image:: tex
:alt: tex: \xi_i
|khh10| and try to use as few non-zero as possible (use penalty term)
.. |khh10| image:: tex
:alt: tex: \vec{c} \cdot y_i \geq 1 \Rightarrow \vec{c} \cdot y_i \geq 1 - \xi _i
Quadratic Optimization Problem
==========
minimize |khh11|
subject to |khh12|
.. |khh11| image:: tex
:alt: tex: \frac{1}{2}||\vec{c}||^2 + constant \displaystyle \sum_{i=1}^{d} \xi _i
.. |khh12| image:: tex
:alt: tex: \vec{c} \cdot y_i \geq 1 - \xi _i, \quad \forall{i}
The Kernel Trick
==
Proposed by Aizerman in another context used by Vapnik,Boser, Guyon to upgrade [SVM] to find non-linear decision boundary based on observation that [SVM] training only introduces |khh5|
|khh13|
.. |khh13| image:: tex
- alt: tex: y_i \cdot y_j = \varphi (x_i) \cdot \varphi (x_j)
A kernel function |khh14| for a given mapping |khh15| is a function such that |khh16|.
.. |khh14| image:: tex
- alt: tex: K:\Re ^k \times \Re ^k \rightarrow \Re
.. |khh15| image:: tex
- alt: tex: \varphi
.. |khh16| image:: tex
- alt: tex: K(x,x')=\varphi (x) \cdot \varphi (x')
Therefore, |khh17| -> No need to compute |khh18| and no need to know |khh15|
.. |khh17| image:: tex
- alt: tex: y_i \cdot y_j = K(x_i,x_j)
.. |khh18| image:: tex
- alt: tex: \varphi (x_i), \varphi (x_j)
In order to exploit kernel trick, we need to have good kernel functions. One way to do that is to choose |fx| (called basis functions) and use it to find corresponding kernel. Another method is to construct kernel functions directly by making sure that the function is a valid kernel which means it corresponds to a scalar product in some feature space.
Necessary and sufficient condition for a function to be a valid kernel is Gram Matrix K whose elements are |kxx| to be positive semidefinite. Here are some figures to show the general characteristics of a kernel function.
.. |fx| image:: tex
- alt: tex: \varphi (x)
.. |kxx| image:: tex
- alt: tex: k(x_n, x_m)
.. image:: kernel.jpg
The left hand side figure represents the set of basis functions, and the right hand side represents the Gaussian Kernel Function.
A powerful method for creating good kernel functions is to use simpler kernel functions to build new ones. Because, we can manipulate kernel functions by using some transformations such as scalar multiplications, summing two kernel functions, inserting kernel functions to some other functions and so on.
2 Nice examples can be found in [Support Vector Machines : 1-D Example] and [SVM: 2-D Example]
One example of kernel functions
take |L13_1|
then, |L13_2|
|L13_2_2|
Here kernel is |L13_3|
Note : K is kernel for other functions |L13_4|
(for example |L13_5|
one-to-one correspondence between kernel and mapping |L13_4| s
.. |L13_1| image:: tex
- alt: tex: \varphi (x_1 , x_2)=(x_1^2,\sqrt{2} x_1 x_2, x_2^2 )
.. |L13_2| image:: tex
- alt: tex: \varphi (x_1 , x_2) \varphi (\acute{x_1} , \acute{x_2})=x_1^2 \acute{x_1^2}+2x_1 x_2 \acute{x_1} \acute{x_2} + x_2^2 \acute{x_2^2}
.. |L13_2_2| image:: tex
- alt: tex: (x_1^2 \acute{x_1^2} + x_2^2 \acute{x_2^2} )^2 = [(x_1, x_2) (\acute{x_1^2}, \acute{x_2^2})]^2
.. |L13_3| image:: tex
- alt: tex: K(\vec x, \acute{\vec x} ) = (\vec x, \acute{\vec x} )^2
.. |L13_4| image:: tex
- alt: tex: \varphi
.. |L13_5| image:: tex
- alt: tex: \varphi (x_1 , x_2) = \frac {1}{\sqrt{2}} (x_1^2 - x_2^2, 2x_1^2 x_2^2, x_1^2 + x_2^2)