m |
(→Definition) |
||
| Line 4: | Line 4: | ||
| − | === | + | === Support Vector Machines === |
| + | (Continued from [[Lecture 11 - Fischer's Linear Discriminant again_OldKiwi|Lecture 11]]) | ||
| + | |||
| + | *Definition | ||
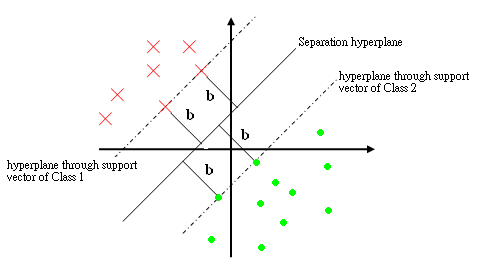
The support vectors are the training points <math>y_i</math> such that <math>\vec{c}\cdot{y_i}=b,\forall{i}</math>. i.e. they are the closest to the hyperplane. | The support vectors are the training points <math>y_i</math> such that <math>\vec{c}\cdot{y_i}=b,\forall{i}</math>. i.e. they are the closest to the hyperplane. | ||
| Line 10: | Line 13: | ||
[[Image:Lec12_sv_pic_OldKiwi.PNG]] | [[Image:Lec12_sv_pic_OldKiwi.PNG]] | ||
| + | |||
| + | |||
| + | *How to Train a Support Vector Machine (SVM) | ||
| + | |||
| + | We want to find a <math>\vec{c}</math> such that <math>\vec{c}\cdot{y_i} \geq b, \forall{i}</math>. This however, is wishful thinking, so we try to find this for as many training samples as possible with <math>b</math> as large as possible. | ||
| + | |||
| + | Observe: If <math>\vec{c}</math> is a solution with margin <math>b</math>, then <math>\alpha\vec{c}</math> is a solution with margin <math>\alpha b, \forall{\alpha} \in \Re > 0</math> | ||
| + | |||
| + | So to pose the problem well, we demand that <math>\vec{c}\cdot{y_i} \geq 1, '\forall{i}' </math> and try to minimize <math>\vec{c}</math> | ||
Revision as of 17:23, 19 March 2008
Support Vector Machines
(Continued from Lecture 11)
- Definition
The support vectors are the training points $ y_i $ such that $ \vec{c}\cdot{y_i}=b,\forall{i} $. i.e. they are the closest to the hyperplane.
- How to Train a Support Vector Machine (SVM)
We want to find a $ \vec{c} $ such that $ \vec{c}\cdot{y_i} \geq b, \forall{i} $. This however, is wishful thinking, so we try to find this for as many training samples as possible with $ b $ as large as possible.
Observe: If $ \vec{c} $ is a solution with margin $ b $, then $ \alpha\vec{c} $ is a solution with margin $ \alpha b, \forall{\alpha} \in \Re > 0 $
So to pose the problem well, we demand that $ \vec{c}\cdot{y_i} \geq 1, '\forall{i}' $ and try to minimize $ \vec{c} $