| Line 33: | Line 33: | ||
<math>y[n] = \sum a_{k} H(e^{jk \omega_{o}}) e^{jk \omega_{o}n} = \sum_{k=0}^{3} a_{k} H(e^{jk \frac{\pi}{2}}) e^{jk \frac{\pi}{2}n} = \sum_{k=0}^{3} a_{k} (1 + 2 e^{-jk \frac{\pi}{2}}) e^{jk \frac{\pi}{2}n} = (1)(3)(1) + (-\frac{1}{2})(-1)e^{j \frac{\pi}{2} n} + 0 + (-\frac{1}{2})(3)e^{j \frac{3 \pi}{2}n}</math> | <math>y[n] = \sum a_{k} H(e^{jk \omega_{o}}) e^{jk \omega_{o}n} = \sum_{k=0}^{3} a_{k} H(e^{jk \frac{\pi}{2}}) e^{jk \frac{\pi}{2}n} = \sum_{k=0}^{3} a_{k} (1 + 2 e^{-jk \frac{\pi}{2}}) e^{jk \frac{\pi}{2}n} = (1)(3)(1) + (-\frac{1}{2})(-1)e^{j \frac{\pi}{2} n} + 0 + (-\frac{1}{2})(3)e^{j \frac{3 \pi}{2}n}</math> | ||
| − | <math>= 3 + \frac{1}{2} | + | <math>= 3 + \frac{1}{2}e^{j \frac{\pi}{2} n} + -\frac{3}{2}e^{j \frac{3 \pi}{2}n}</math> |
Revision as of 22:16, 23 September 2008
Contents
DT LTI System
$ y[n] = x[n] + 2x[n-1] $
h[n]
$ h[n] = \delta [n] + 2 \delta [n-1] $
H(z)
$ H(z) = \sum_{m=-\infty}^{\infty}h[m] e^{-j \omega m} = \sum_{m=-\infty}^{\infty} (\delta [m] + 2 \delta [m-1]) e^{-j \omega m} = \sum_{m=-\infty}^{\infty} \delta [m] e^{-j \omega m} + \sum_{m=-\infty}^{\infty} 2 \delta [m-1] e^{-j \omega m} = 1 + 2 e^{-j \omega} $
Response to x[n]
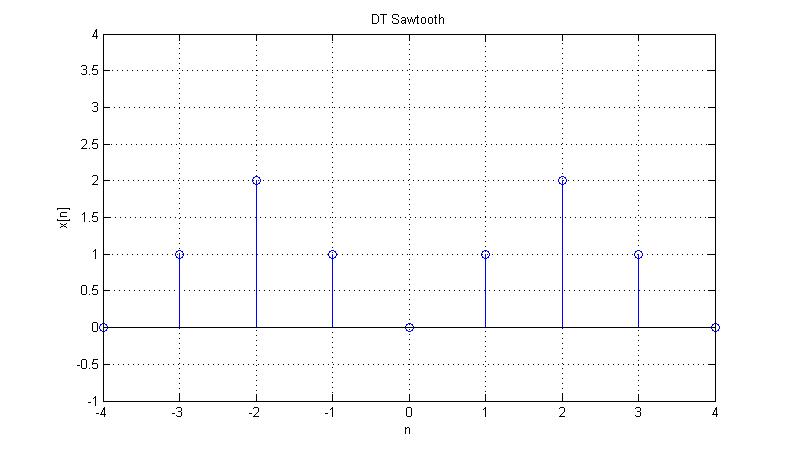
Input $ x[n] $ is the following signal:
The Fourier series coefficients for $ x[n] $ are:
$ a_{0} = 1 $
$ a_{1} = -\frac{1}{2} $
$ a_{2} = 0 $
$ a_{3} = -\frac{1}{2} $
$ y[n] = \sum a_{k} H(e^{jk \omega_{o}}) e^{jk \omega_{o}n} = \sum_{k=0}^{3} a_{k} H(e^{jk \frac{\pi}{2}}) e^{jk \frac{\pi}{2}n} = \sum_{k=0}^{3} a_{k} (1 + 2 e^{-jk \frac{\pi}{2}}) e^{jk \frac{\pi}{2}n} = (1)(3)(1) + (-\frac{1}{2})(-1)e^{j \frac{\pi}{2} n} + 0 + (-\frac{1}{2})(3)e^{j \frac{3 \pi}{2}n} $
$ = 3 + \frac{1}{2}e^{j \frac{\pi}{2} n} + -\frac{3}{2}e^{j \frac{3 \pi}{2}n} $