Basic definition of the Z-Transform
The Z-transform of a sequence is defined as $ H(z) = \sum^{\infty}_{n = -\infty} h[n]z^{-n} $
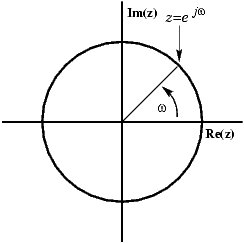
The complex plane
In order to get further insight into the relationship between the Fourier Transform and the Z-Transform it is useful to look at the complex plane or z-plane. Take a look at the complex plane:
The Z-plane is a complex plane with an imaginary and real axis referring to the complex-valued variable z. The position on the complex plane is given by rⅇⅈω , and the angle from the positive, real axis around the plane is denoted by ω. X(z) is defined everywhere on this plane. X(ⅇⅈω) on the other hand is defined only where |z|=1, which is referred to as the unit circle. So for example, ω=1 at z=1 and ω=<apply>π</apply> at z=-1. This is useful because, by representing the Fourier transform as the z-transform on the unit circle, the periodicity of Fourier transform is easily seen.
Region of Convergence
The region of convergence, known as the ROC, is important to understand because it defines the region where the z-transform exists. The ROC for a given x[n] , is defined as the range of z for which the z-transform converges. Since the z-transform is a power series, it converges when x[n]z−n is absolutely summable. Stated differently,
∞ ∑ n=−∞ (|x[n]z−n|)<∞ (4) must be satisfied for convergence. This is best illustrated by looking at the different ROC's of the z-transforms of αnu[n] and αnu[n−1].