(→Non-periodic Functions) |
(→Periodic Functions) |
||
| Line 5: | Line 5: | ||
A Discrete Time signal is said to be periodic if there exists <math>\ N > 0</math> (where N is an integer) such that <math>\ x[n+N]=x[n]</math> | A Discrete Time signal is said to be periodic if there exists <math>\ N > 0</math> (where N is an integer) such that <math>\ x[n+N]=x[n]</math> | ||
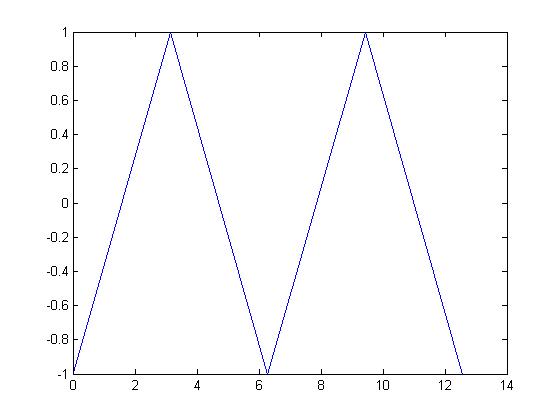
| − | An example of a CT periodic signal is <math>x(t) = sawtooth(t)</math>: | + | An example of a CT periodic signal is <math>x(t) = sawtooth(t,.5)</math> (which is actually a tri wave): |
| − | [[Image: | + | [[Image:tri_ECE301Fall2008mboutin.jpg]] |
As you can see the function has a fundamental period of two Pi. Therefore any multiple of two Pi is a period. | As you can see the function has a fundamental period of two Pi. Therefore any multiple of two Pi is a period. | ||
Latest revision as of 12:21, 5 September 2008
Periodic Functions
A Continuous Time signal is said to be periodic if there exists $ \ T > 0 $ such that $ \ x(t+T)=x(t) $
A Discrete Time signal is said to be periodic if there exists $ \ N > 0 $ (where N is an integer) such that $ \ x[n+N]=x[n] $
An example of a CT periodic signal is $ x(t) = sawtooth(t,.5) $ (which is actually a tri wave):
As you can see the function has a fundamental period of two Pi. Therefore any multiple of two Pi is a period.
Non-periodic Functions
A Continuous Time signal is said to be non-periodic if there is no value of $ \ T > 0 $ that satisfies $ \ x(t+T)=x(t) $
A Discrete Time signal is said to be non-periodic if there is no value of $ \ N > 0 $ (where N is an integer) that satisfies$ \ x[n+N]=x[n] $
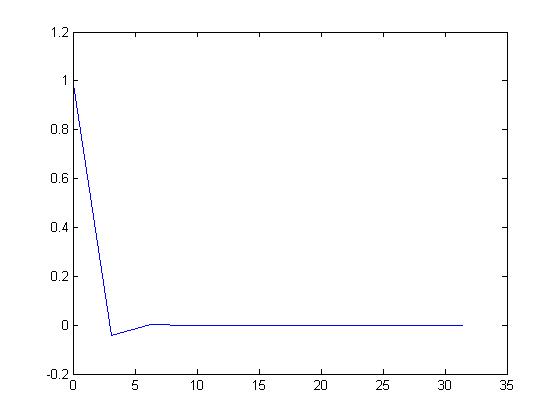
An example of a non-periodic continuous time signal would be $ \ x(t) = e^{(-1 + j)t} $. This goes to show that not all complex exponential functions are periodic.
Here is what the function looks like when graphed:
As you can see from the graph the function is non-periodic.