(→The polar form) |
(→Complex Arithmetic) |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Notation == | == Notation == | ||
| − | <math> | + | <math> z+yi </math> |
| − | where a and b are real numbers, and i is the imaginary unit, which has the property <math>i^2 = -1</math>. The real number | + | where a and b are real numbers, and i is the imaginary unit, which has the property <math>i^2 = -1</math>. The real number x is called the real part of the complex number, and the real number y is the imaginary part. |
| + | |||
| + | == Complex Plane == | ||
| + | The complex plane provides a way to express complex numbers graphically. Any complex number can be expressed as a point on the complex plane. | ||
| + | [[Image:cplane2_ECE301Fall2008mboutin.png]] | ||
== Complex Arithmetic == | == Complex Arithmetic == | ||
| Line 17: | Line 21: | ||
<math> \frac{(a + bi)}{(c + di)} = \left({ac + bd \over c^2 + d^2}\right) + \left( {bc - ad \over c^2 + d^2} \right)i\ </math> | <math> \frac{(a + bi)}{(c + di)} = \left({ac + bd \over c^2 + d^2}\right) + \left( {bc - ad \over c^2 + d^2} \right)i\ </math> | ||
| + | |||
| + | == The polar form == | ||
| + | |||
| + | The polar form is <math> z = r\,(\cos \varphi + i\sin \varphi )\,</math>. | ||
| + | |||
| + | It can also be represented as Euler's formula <math> z = r\,\mathrm{e}^{i \varphi}\,</math> | ||
Latest revision as of 11:29, 5 September 2008
Notation
$ z+yi $ where a and b are real numbers, and i is the imaginary unit, which has the property $ i^2 = -1 $. The real number x is called the real part of the complex number, and the real number y is the imaginary part.
Complex Plane
The complex plane provides a way to express complex numbers graphically. Any complex number can be expressed as a point on the complex plane.
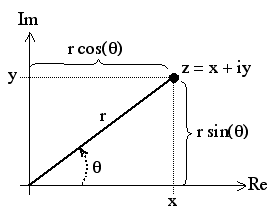
Complex Arithmetic
Addition and Subtraction
$ (a + bi) + (c + di) = (a + c) + (b + d)i $
$ (a + bi) - (c + di) = (a - c) + (b - d)i $
Multiplication
$ (a + bi) * (c + di) = (ac - bd) + (ad + bc)i $
Division
$ \frac{(a + bi)}{(c + di)} = \left({ac + bd \over c^2 + d^2}\right) + \left( {bc - ad \over c^2 + d^2} \right)i\ $
The polar form
The polar form is $ z = r\,(\cos \varphi + i\sin \varphi )\, $.
It can also be represented as Euler's formula $ z = r\,\mathrm{e}^{i \varphi}\, $

