| Line 1: | Line 1: | ||
| − | More Traversals of a Graph or Digraph<br>• Tour – visit each vertex in a graph exactly once and finish at the vertex started from.<br>• Eulerian tour – find a path/tour through the graph such that every edge is visited<br>exactly once. (Easy – check nodal degree; if all are even, it is possible.)<br>• Hamiltonian tour – find a path through the graph such that every vertex is visited<br>exactly once. (NP complete)<br>• See Figure 5 for different tours. | + | The Greedy Method<br>Introduction<br>• We have completed data structures.<br>• We now are going to look at algorithm design methods.<br>• Often we are looking at optimization problems whose performance is exponential.<br>• For an optimization problem, we are given a set of constraints and an optimization<br>function.<br>o Solutions that satisfy the constraints are called feasible solutions.<br>o A feasible solution for which the optimization function has the best possible value<br>is called an optimal solution.<br>• Cheapest lunch possible: Works by getting the cheapest meat, fruit, vegetable, etc.<br>• In a greedy method we attempt to construct an optimal solution in stages.<br>o At each stage we make a decision that appears to be the best (under some criterion) at the time.<br>o A decision made at one stage is not changed in a later stage, so each decision should assure feasibility.<br>• Consider getting the best major: What is best now, may be worst later.<br>• Consider change making: Given a coin system and an amount to make change for, we<br>want minimal number of coins.<br>o A greedy criterion could be, at each stage increase the total amount of change<br>constructed as much as possible.<br> In other words, always pick the coin with the greatest value at every step.<br>o A greedy solution is optimal for some change systems. • Machine scheduling:<br>o Have a number of jobs to be done on a minimum number of machines. Each job has a start and end time.<br>o Order jobs by start time.<br>o If an old machine becomes available by the start time of the task to be assigned,<br>assign the task to this machine; if not assign it to a new machine. o This is an optimal solution.<br>• Note that our Huffman tree algorithm is an example of a greedy algorithm: o Pick least weight trees to combine.<br>• Heuristic – we are not willing to take the time to get an optimal solution, but we can be satisfied with a “pretty good” solution.<br>0/1 Knapsack Problem<br>• Problem description:<br>o Pack a knapsack with a capacity of c. |
| + | |||
| + | o From a list of n items, we must select the items that are to be packed in the knapsack.<br>o Each object i has a weight of wi and a profit of pi .<br>• In a feasible knapsack packing, the sum of the weights packed does not exceed the<br>knapsack capacity.<br>• An optimal packing is a feasible one with maximum profit – ∑ p x subject to the constraints ∑wx ≤c and x ∈{0,1},1≤i≤n<br> o We are to find the values of xi where xi =1 if object i is packed into the knapsack and xi = 0 if object i is not packed.<br>• Greedy strategies for this problem:<br>o From the remaining objects, select the object with maximum profit that fits into<br>the knapsack.<br>o From the remaining objects, select the one that has minimum weight and also fits<br>into the knapsack.<br>o From the remaining objects, select the one with maximum pi / wi that fits into the<br>knapsack.<br>• Consideraknapsackinstancewheren=4, w=[2,4,6,7], p=[6,10,12,13],and c=11.<br>o Look at the above three strategies.<br>• None of the above algorithms can guarantee the optimal solution.<br>o This is not surprising since this problem is a NP-hard problem.<br>• Of the above three algorithms, the third one is probably the best heuristic.<br>Topological Ordering<br>• Greedy criteria – for the unnumbered nodes, assign a number to a node for which all predecessors have been numbered.<br>• Algorithm – Initially, for each node with predecessor count of zero, put it in a container (stack, queue, anything will do).<br>1. Remove a node with predecessor count of zero from the container, number it, then list it.<br>2. For each successor, decrement its predecessor count.<br>3. If a successor now has a predecessor count of zero, add it to the container.<br>• Complexity – assume an adjacency list.<br>1. Find predecessor count. Ο(e) , where e is number of edges.<br>2. List node – for each successor, update predecessor count. Ο(e + n) , since if have<br>lots of nodes with no predecessors, n could be more than e.<br>Matchings and Coverings in a Graph | ||
| + | |||
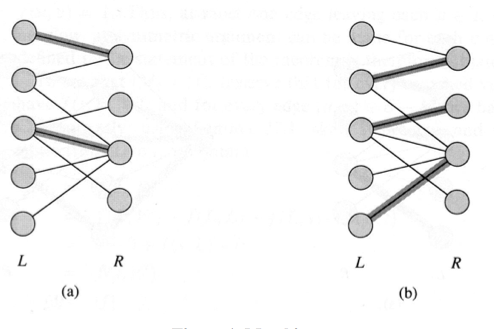
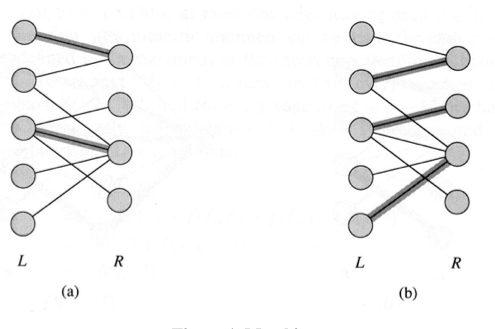
| + | • Matching – a set of edges, no two of which have a vertex in common.<br>• A perfect match is one in which all vertices are matched.<br>• A maximum matching is matching that cannot be extended by the addition of an edge.<br>• For an example see Figure 1.<br> | ||
| + | |||
| + | [[Image:Maoyi2.png]] | ||
| + | |||
| + | <br> | ||
| + | |||
| + | More Traversals of a Graph or Digraph<br>• Tour – visit each vertex in a graph exactly once and finish at the vertex started from.<br>• Eulerian tour – find a path/tour through the graph such that every edge is visited<br>exactly once. (Easy – check nodal degree; if all are even, it is possible.)<br>• Hamiltonian tour – find a path through the graph such that every vertex is visited<br>exactly once. (NP complete)<br>• See Figure 5 for different tours. | ||
[[Image:Maoyi.png]] | [[Image:Maoyi.png]] | ||
Revision as of 14:32, 16 April 2012
The Greedy Method
Introduction
• We have completed data structures.
• We now are going to look at algorithm design methods.
• Often we are looking at optimization problems whose performance is exponential.
• For an optimization problem, we are given a set of constraints and an optimization
function.
o Solutions that satisfy the constraints are called feasible solutions.
o A feasible solution for which the optimization function has the best possible value
is called an optimal solution.
• Cheapest lunch possible: Works by getting the cheapest meat, fruit, vegetable, etc.
• In a greedy method we attempt to construct an optimal solution in stages.
o At each stage we make a decision that appears to be the best (under some criterion) at the time.
o A decision made at one stage is not changed in a later stage, so each decision should assure feasibility.
• Consider getting the best major: What is best now, may be worst later.
• Consider change making: Given a coin system and an amount to make change for, we
want minimal number of coins.
o A greedy criterion could be, at each stage increase the total amount of change
constructed as much as possible.
In other words, always pick the coin with the greatest value at every step.
o A greedy solution is optimal for some change systems. • Machine scheduling:
o Have a number of jobs to be done on a minimum number of machines. Each job has a start and end time.
o Order jobs by start time.
o If an old machine becomes available by the start time of the task to be assigned,
assign the task to this machine; if not assign it to a new machine. o This is an optimal solution.
• Note that our Huffman tree algorithm is an example of a greedy algorithm: o Pick least weight trees to combine.
• Heuristic – we are not willing to take the time to get an optimal solution, but we can be satisfied with a “pretty good” solution.
0/1 Knapsack Problem
• Problem description:
o Pack a knapsack with a capacity of c.
o From a list of n items, we must select the items that are to be packed in the knapsack.
o Each object i has a weight of wi and a profit of pi .
• In a feasible knapsack packing, the sum of the weights packed does not exceed the
knapsack capacity.
• An optimal packing is a feasible one with maximum profit – ∑ p x subject to the constraints ∑wx ≤c and x ∈{0,1},1≤i≤n
o We are to find the values of xi where xi =1 if object i is packed into the knapsack and xi = 0 if object i is not packed.
• Greedy strategies for this problem:
o From the remaining objects, select the object with maximum profit that fits into
the knapsack.
o From the remaining objects, select the one that has minimum weight and also fits
into the knapsack.
o From the remaining objects, select the one with maximum pi / wi that fits into the
knapsack.
• Consideraknapsackinstancewheren=4, w=[2,4,6,7], p=[6,10,12,13],and c=11.
o Look at the above three strategies.
• None of the above algorithms can guarantee the optimal solution.
o This is not surprising since this problem is a NP-hard problem.
• Of the above three algorithms, the third one is probably the best heuristic.
Topological Ordering
• Greedy criteria – for the unnumbered nodes, assign a number to a node for which all predecessors have been numbered.
• Algorithm – Initially, for each node with predecessor count of zero, put it in a container (stack, queue, anything will do).
1. Remove a node with predecessor count of zero from the container, number it, then list it.
2. For each successor, decrement its predecessor count.
3. If a successor now has a predecessor count of zero, add it to the container.
• Complexity – assume an adjacency list.
1. Find predecessor count. Ο(e) , where e is number of edges.
2. List node – for each successor, update predecessor count. Ο(e + n) , since if have
lots of nodes with no predecessors, n could be more than e.
Matchings and Coverings in a Graph
• Matching – a set of edges, no two of which have a vertex in common.
• A perfect match is one in which all vertices are matched.
• A maximum matching is matching that cannot be extended by the addition of an edge.
• For an example see Figure 1.
More Traversals of a Graph or Digraph
• Tour – visit each vertex in a graph exactly once and finish at the vertex started from.
• Eulerian tour – find a path/tour through the graph such that every edge is visited
exactly once. (Easy – check nodal degree; if all are even, it is possible.)
• Hamiltonian tour – find a path through the graph such that every vertex is visited
exactly once. (NP complete)
• See Figure 5 for different tours.