| (5 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
<center> <math> \frac{a+b}{a} = \frac{a}{b} </math> </center> | <center> <math> \frac{a+b}{a} = \frac{a}{b} </math> </center> | ||
| − | + | That is, the ratio between the sum of two components and the larger component, and the ratio between the larger component and smaller component is the same. This is the golden ratio. | |
| − | + | After solving for the ratio itself (discussed in the calculations section), we can find that the golden ratio is: | |
| − | <center> <math> | + | <center> <math> \frac{1 \pm \sqrt{5}}{2} = \phi = 1.61803398875 </math> </center> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
The golden ratio, <math>\phi</math>, is sometimes also called the golden mean or the golden section. The golden ratio can be frequently observed in man-made objects, though they are generally “imperfectly golden” – that is, the ratio is approximately the golden ratio, but not exactly. Some everyday examples include: credit cards, <math>\frac{w}{h}=1.604</math>, and laptop screens, <math>\frac{w}{h}=1.602</math> (Tannenbaum 392). | The golden ratio, <math>\phi</math>, is sometimes also called the golden mean or the golden section. The golden ratio can be frequently observed in man-made objects, though they are generally “imperfectly golden” – that is, the ratio is approximately the golden ratio, but not exactly. Some everyday examples include: credit cards, <math>\frac{w}{h}=1.604</math>, and laptop screens, <math>\frac{w}{h}=1.602</math> (Tannenbaum 392). | ||
| Line 40: | Line 18: | ||
[https://www.mathsisfun.com/numbers/golden-ratio.html MathIsFun] also has an interactive display that can construct a rectangle in the golden ratio given a certain fixed width or length. | [https://www.mathsisfun.com/numbers/golden-ratio.html MathIsFun] also has an interactive display that can construct a rectangle in the golden ratio given a certain fixed width or length. | ||
| + | |||
| + | [[Walther MA279 Fall2018 topic2|Back to Home]] | ||
| + | <br><br>[[Category:MA279Fall2018Walther]] | ||
Latest revision as of 17:49, 2 December 2018
Introduction
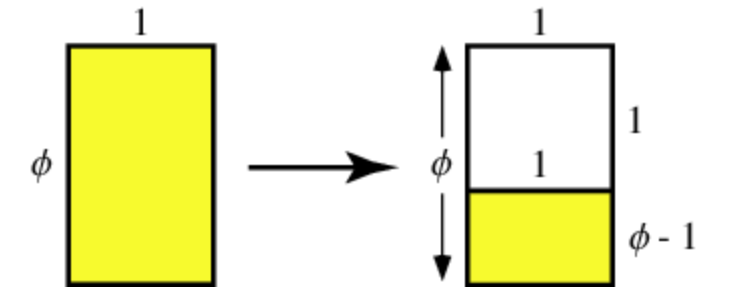
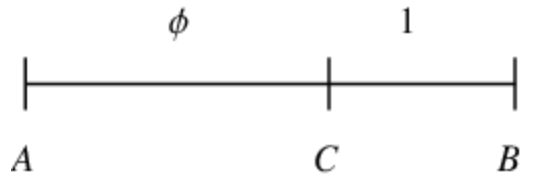
The golden ratio is a ratio such that, given two quantities a and b,
That is, the ratio between the sum of two components and the larger component, and the ratio between the larger component and smaller component is the same. This is the golden ratio.
After solving for the ratio itself (discussed in the calculations section), we can find that the golden ratio is:
The golden ratio, $ \phi $, is sometimes also called the golden mean or the golden section. The golden ratio can be frequently observed in man-made objects, though they are generally “imperfectly golden” – that is, the ratio is approximately the golden ratio, but not exactly. Some everyday examples include: credit cards, $ \frac{w}{h}=1.604 $, and laptop screens, $ \frac{w}{h}=1.602 $ (Tannenbaum 392).
Visualizations of the golden ratio can be seen below (Weisstein):
MathIsFun also has an interactive display that can construct a rectangle in the golden ratio given a certain fixed width or length.