(Created page with "<math> \begin{equation*} \boxed{d\bar{H}=\frac{I(\bar{R}')d\bar{l}'\times(\bar{R}-\bar{R}')}{4\pi\abs{\bar{R}-\bar{R}'}^3}} \end{equation*} </math> <math> \begin{align*} \tex...") |
|||
| Line 1: | Line 1: | ||
| + | 2) | ||
| + | |||
<math> | <math> | ||
\begin{equation*} | \begin{equation*} | ||
| − | \ | + | \text{\underline{Biot-Savart}:} \qquad \qquad d\bar{H}=\frac{I(\bar{R})d\bar{l}\times(\bar{R}-\bar{R}')}{4\pi\abs{\bar{R}-\bar{R}'}^3} |
\end{equation*} | \end{equation*} | ||
</math> | </math> | ||
| + | |||
| + | [[Image:biot.jpg|Alt text|270x222px]] | ||
<math> | <math> | ||
\begin{align*} | \begin{align*} | ||
| − | + | \bar{R}&= 0\hat{x}+0\hat{y}+0\hat{z}\\ | |
| − | + | \bar{R}'&=y\hat{y}\\ | |
| − | + | \abs{\bar{R}-\bar{R}'}&=y \\ | |
| − | + | d\bar{l}&= (dy)\hat{y} | |
| − | + | ||
| − | + | ||
\end{align*} | \end{align*} | ||
</math> | </math> | ||
| Line 18: | Line 20: | ||
<math> | <math> | ||
\begin{equation*} | \begin{equation*} | ||
| − | \ | + | d\bar{H}=\frac{(Idy)\hat{y}\times(-y\hat{y})}{4\pi\abs{y}^3}=0 \longrightarrow \boxed{\bar{H}=0} |
\end{equation*} | \end{equation*} | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \begin{align*} | ||
| + | \text{\underline{Ampere}:}& & \nabla\times\bar{H}&=\bar{J} & &\longrightarrow& & \oint \bar{H}\cdot d\bar{l}&=I_{enc}\\ | ||
| + | \text{at the origin:}& & I_{enc}&=0 & &\longrightarrow& & \boxed{\bar{H}=0} | ||
| + | \end{align*} | ||
</math> | </math> | ||
Revision as of 19:43, 18 June 2017
2)
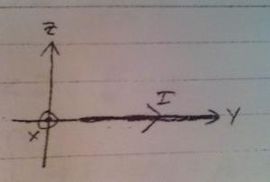
$ \begin{equation*} \text{\underline{Biot-Savart}:} \qquad \qquad d\bar{H}=\frac{I(\bar{R})d\bar{l}\times(\bar{R}-\bar{R}')}{4\pi\abs{\bar{R}-\bar{R}'}^3} \end{equation*} $
$ \begin{align*} \bar{R}&= 0\hat{x}+0\hat{y}+0\hat{z}\\ \bar{R}'&=y\hat{y}\\ \abs{\bar{R}-\bar{R}'}&=y \\ d\bar{l}&= (dy)\hat{y} \end{align*} $
$ \begin{equation*} d\bar{H}=\frac{(Idy)\hat{y}\times(-y\hat{y})}{4\pi\abs{y}^3}=0 \longrightarrow \boxed{\bar{H}=0} \end{equation*} $
$ \begin{align*} \text{\underline{Ampere}:}& & \nabla\times\bar{H}&=\bar{J} & &\longrightarrow& & \oint \bar{H}\cdot d\bar{l}&=I_{enc}\\ \text{at the origin:}& & I_{enc}&=0 & &\longrightarrow& & \boxed{\bar{H}=0} \end{align*} $