| Line 9: | Line 9: | ||
Imaging systems are well approximated by linear space invariant systems theory, which is why we will use it to describe imaging systems. | Imaging systems are well approximated by linear space invariant systems theory, which is why we will use it to describe imaging systems. | ||
| − | [[Image:PSF1.jpeg|500px|thumb|Imaging a Point Source]] | + | [[Image:PSF1.jpeg|500px|thumb|Fig 1.1: Imaging a Point Source]] |
| Line 30: | Line 30: | ||
</math> | </math> | ||
| − | + | So if you take away the magnification factor, the resulting image is like the convolution of what the image should have been with the PSF of the system. | |
| − | + | Alternatively you could define the function | |
| − | + | <math>\tilde{f}(x,y) := f(\frac{\xi}{M},\frac{\eta}{M})</math> | |
| − | + | Then the imaging system acts like a 2_D convolution where | |
| − | + | <math> g(x,y) = \frac{1}{M^{2}} h(x,y)* \tilde{f} (x,y)</math> | |
| − | + | Real imaging systems are not perfectly space invariant so as you move around on the image plain the PSF will vary. You can observe this if you go out on a starry evening and place a camera on a tripod and look at some of the starts in the sky. The stars are like perfect point sources. The image you capture with your camera will have points on it but if you zoom in on a point using your computer, you will notice that the image is not really a point; it will be a blur spanning a cluster of pixels. If you use different apertures, you will also notice that for larger f-stop, you get a bigger blur and vice versa. | |
| − | + | So now you have essentially put the delta function, <math>\delta (x,y)</math>, through your system to obtain the PSF because the star is like a delta function. If you take the Fourier transform of that you will get the frequency response of the system. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | <math> | + | |
| − | \ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | </math> | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Now let's say that the PSF of the system is described by an Airy function. For a space invariant and hence isotropic system you might get a PSF as shown in figure 1.2 and the PSFs for all the stars would be identical assuming identical brightness (see figure 1.3A). But if your imaging system is, say, anisotropic, the different stars would have different PSFs depending where they appear in your actual image (see figure 1.3B). | |
| − | + | [[Image:PSF2.jpeg|500px|thumb|Fig 1.2: 2-D Impulse Response of System]] | |
| − | |||
| − | + | [[Image:PSF3.jpeg|600px|thumb|Fig 1.3: Isotropic and Anisotropic PSFs]] | |
Revision as of 18:13, 30 March 2013
Space Domain Models for Optical Imaging Systems
keyword: ECE 637, digital image processing
Imaging systems are well approximated by linear space invariant systems theory, which is why we will use it to describe imaging systems.
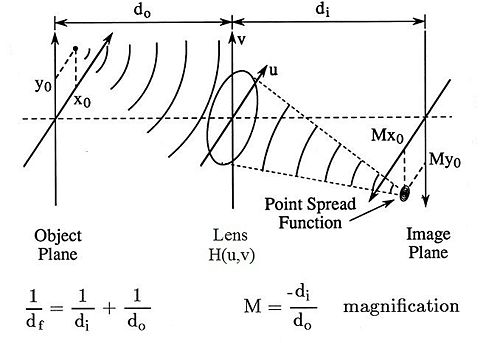
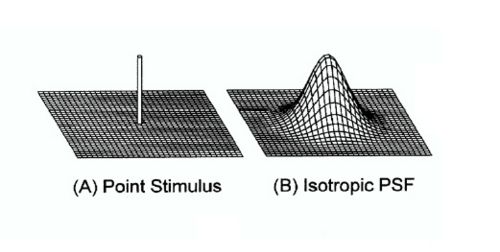
We can characterize the lens for a given aperture by its impulse response. Its Point Spread Function (PSF) is analogous to its impulse response since the PSF describes the system's response to a point input (think about a point input as $ \delta (x,y) $).
The PSF will be denoted by the function $ h(x,y) $ in the space domain. Its CSFT will be given by $ H(u,v) $.
Ideally, a point input, would be represented in an image as a single pixel. Let this ideal image be $ f(x,y) $. Consider this to be the input to your imaging system.
Your actual image of the point input however, will be reproduced as something other that a single pixel. This is the output of your imaging system. Let the output of the system be $ g(x,y) $.
So the image you form on the focal plane array is given by the convolution of the ideal image you should have formed with the PSF of the system.
$ \begin{align} g(x,y) &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(\xi,\eta)h(x-M\xi,y-M\eta)d\xi d\eta \\ &= \frac{1}{M^2} \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(\frac{\xi}{M},\frac{\eta}{M})h(x-\xi,y-\eta)d\xi d\eta \end{align} $
So if you take away the magnification factor, the resulting image is like the convolution of what the image should have been with the PSF of the system.
Alternatively you could define the function
$ \tilde{f}(x,y) := f(\frac{\xi}{M},\frac{\eta}{M}) $
Then the imaging system acts like a 2_D convolution where
$ g(x,y) = \frac{1}{M^{2}} h(x,y)* \tilde{f} (x,y) $
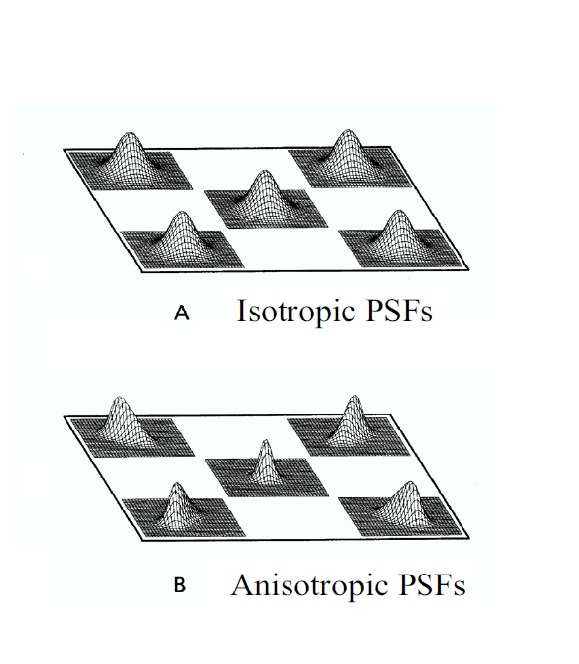
Real imaging systems are not perfectly space invariant so as you move around on the image plain the PSF will vary. You can observe this if you go out on a starry evening and place a camera on a tripod and look at some of the starts in the sky. The stars are like perfect point sources. The image you capture with your camera will have points on it but if you zoom in on a point using your computer, you will notice that the image is not really a point; it will be a blur spanning a cluster of pixels. If you use different apertures, you will also notice that for larger f-stop, you get a bigger blur and vice versa.
So now you have essentially put the delta function, $ \delta (x,y) $, through your system to obtain the PSF because the star is like a delta function. If you take the Fourier transform of that you will get the frequency response of the system.
Now let's say that the PSF of the system is described by an Airy function. For a space invariant and hence isotropic system you might get a PSF as shown in figure 1.2 and the PSFs for all the stars would be identical assuming identical brightness (see figure 1.3A). But if your imaging system is, say, anisotropic, the different stars would have different PSFs depending where they appear in your actual image (see figure 1.3B).