| Line 56: | Line 56: | ||
So the smaller the <math>d_o</math>, the smaller the reciprocal of <math>d_i</math> and hence the larger <math>d_i</math> is. In other words, as the object plane moves in, the image plane moves out and vice versa. | So the smaller the <math>d_o</math>, the smaller the reciprocal of <math>d_i</math> and hence the larger <math>d_i</math> is. In other words, as the object plane moves in, the image plane moves out and vice versa. | ||
| + | ---- | ||
| + | |||
| + | == Magnification == | ||
| + | |||
| + | Typically, when you view an image through a lens, there is an effective magnification. | ||
| + | |||
| + | [[Image:Lens5.jpeg|400px|thumb|left|Magnification and Inversion of an Image through a Biconvex Lens]] | ||
| + | |||
| + | Let <math>M</math> be the magnification factor of the lens. | ||
| + | |||
| + | For a biconvex lens, | ||
| + | |||
| + | <math>M = -\frac{d_i}{d_o}</math> | ||
| + | |||
| + | The negative sign denotes that for a biconvex lens, the image is also inverted. This phenomena is also illustrated in the above figure. | ||
| + | |||
| + | Normally, the image you form using your camera is much smaller than the actual object. In other words, <math>|M| < 1</math>. So in a typical camera, we have that | ||
| + | |||
| + | <math> d_o >> d_f \ </math> | ||
| + | |||
| + | <math> \Rightarrow d_i = \frac{d_o d_f}{d_o - d_f} \approx d_f</math> | ||
| + | |||
| + | Additionally, if <math>d_i > d_f</math>, then <math>|M| << 1</math>. | ||
| + | |||
| + | However, when the object is closer to the lens than its focal length, <math>|M| > 1</math> and the image is larger than the object. This is the principle used in microscopes to magnify (in absolute terms) objects. | ||
| + | |||
| + | |||
| + | <math> d_i >> d_f \ </math> | ||
| + | |||
| + | <math> \Rightarrow d_o = \frac{d_i d_f}{d_i - d_f} \approx d_f</math> | ||
| + | |||
| + | Additionally, if <math>d_o > d_f</math>, then <math>|M| >> 1</math>. | ||
| + | ---- | ||
| + | |||
| + | == Aperture and f-Stop == | ||
Revision as of 21:18, 28 March 2013
Contents
Lenses in Optical Imaging Systems
keyword: ECE 637, digital image processing
Some Basic Properties and Assumptions
First let's review some basics about lenses. For these notes, we will discuss lenses assuming the thin lens model (i.e. assume that the thickness of the lens is negligible compared to its focal length).
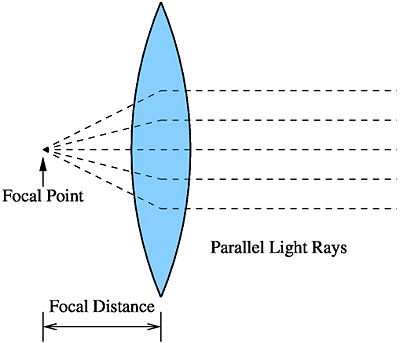
When parallel light rays are incident upon a biconvex lens, they converge at one point after passing through. This point is called the focal point of the lens. The distance from the optical center of the lens to the focal point is called the focal distance.
Note that the focal distance can be different for the two sides of the lens if the lens is not perfectly symmetric.
We can approximate light rays from a star that is many light years away to be parallel but ideally, for a point source to produce perfectly parallel light rays, it would have to be an infinite distance away from your lens.
Image Formation
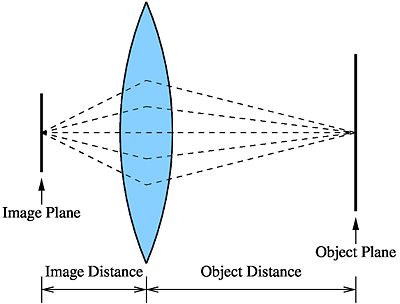
Most of your photography subjects however, will not be an infinite distance away. In that case your object's distance from the lens is some finite quantity and the image plane has to be adjusted so that the image is in focus.
Let $ d_f $ be the focal length of the lens. This quantity is intrinsic to the lens.
Let $ d_o $ be the distance of the object plane from the optical center of the lens.
Let $ d_i $ be the distance of the image plane from the optical center of the lens.
So for your image to be in focus, the following equation must be satisfied.
$ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{d_f} $
Notice that
$ \begin{align} d_o &= \infty \\ \Rightarrow \frac{1}{d_i} &= \frac{1}{d_f} \\ \Rightarrow d_i &= d_f \end{align} $
which is what we stated earlier when defining focal length.
Also note that
$ d_i = (\frac{1}{d_f} - \frac{1}{d_o})^{-1} $
So the smaller the $ d_o $, the smaller the reciprocal of $ d_i $ and hence the larger $ d_i $ is. In other words, as the object plane moves in, the image plane moves out and vice versa.
Magnification
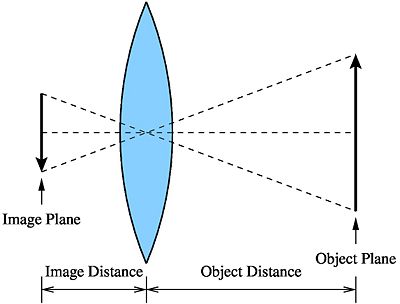
Typically, when you view an image through a lens, there is an effective magnification.
Let $ M $ be the magnification factor of the lens.
For a biconvex lens,
$ M = -\frac{d_i}{d_o} $
The negative sign denotes that for a biconvex lens, the image is also inverted. This phenomena is also illustrated in the above figure.
Normally, the image you form using your camera is much smaller than the actual object. In other words, $ |M| < 1 $. So in a typical camera, we have that
$ d_o >> d_f \ $
$ \Rightarrow d_i = \frac{d_o d_f}{d_o - d_f} \approx d_f $
Additionally, if $ d_i > d_f $, then $ |M| << 1 $.
However, when the object is closer to the lens than its focal length, $ |M| > 1 $ and the image is larger than the object. This is the principle used in microscopes to magnify (in absolute terms) objects.
$ d_i >> d_f \ $
$ \Rightarrow d_o = \frac{d_i d_f}{d_i - d_f} \approx d_f $
Additionally, if $ d_o > d_f $, then $ |M| >> 1 $.