sLecture

↳ Topic 4: Discrete Parameter Signals and Systems

↳ Discrete Transforms

↳ Sampling and Scanning

↳ 2-D Filters

↳ 2-D Random Processes

↳ Filtered Random Processes

↳ Eigen-Signal Analysis and Examples

↳ Supplementary: Proof of Wiener-Khintchine Theorem

Excerpt from Prof. Bouman's Lecture

Discrete Time Fourier Transform (DTFT)

The DTFT is the analogous transform for discrete time signals as the CTFT is for continuous time signals. Let $ x(n) $ be a discrete time signal. Then, its DTFT, $ X(e^{j\omega}) $ is given by
$ X(e^{j\omega}) = \sum_{n = -\infty}^{\infty}x(n)e^{-j\omega n} $
$ x(n) $ can be recovered using the inverse DTFT
$ x(n) = \frac{1}{2\pi}\int_{-\pi}^{\pi}X(e^{j\omega})e^{j\omega n} $

Note that the domain of the DTFT is continuous over (-∞,∞). The DTFT must not be confused with the Discrete Fourier Transform (DFT) which is a transform on a finite length sequence whereas the DTFT is a transform from -∞ to ∞.

Also note that the DTFT is periodic with period $ 2\pi $. Therefore,
$ X(e^{j\omega}) = X(e^{j\omega})\quad \forall \; \omega $
If you know the DTFT of a signal over some interval of length $ 2\pi $, then you know it for all $ \omega $. The periodicity of the DTFT means that functions such as $ rect(\omega) $ are not valid DTFT's.

Some Useful Discrete Time Functions and Transform Pairs

Some of the functions that appear in discrete time analysis will be covered here. For more resources on the DTFT and its properties, you may wish to refer to Rhea's table of formulas concerning the DTFT.

Constant Functions

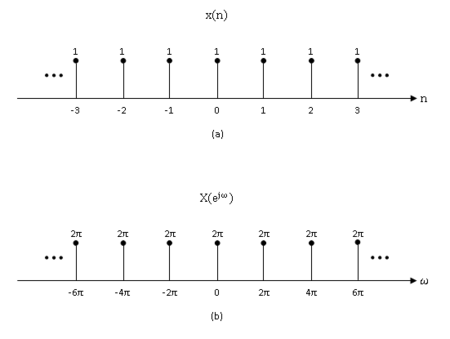
Since the DTFT is a linear transform, I will only cover the simplest case when $ x(n) = 1 $. The DTFT of a constant function produces a pulse train that is periodic with period $ 2\pi $.
$ \begin{align} x(n) &= 1 \\ \Rightarrow X(e^{j\omega}) &= 2\pi\sum_{k=-\infty}^{\infty}\delta(\omega-2\pi k) \end{align} $

Fig 1: The DTFT of $ x(n)=1 $(a) $ x(n) $; (b) $ X(e^{j\omega}) $

It is much simpler to show that the IDTFT of the pulse train is one rather than to show that the DTFT of one is the pulse train.
$ x(n) = \frac{1}{2\pi}\int_{-\pi}^{pi} 2\pi\sum_{k=-\infty}^{\infty}\delta(\omega-2\pi k) $
Since there is only one impulse from the sequence that is present in the $ (-\pi,\pi) $ interval, only one term from the sequence is relevant to the integral, the $ k=0 $ term.
$ x(n) = \frac{1}{2\pi}\int_{-\pi}^{\pi} 2\pi \delta(\omega) = 1_{ \quad \blacksquare} $

The Step Function

The step function is equal to one for all n greater than or equal to zero and zero otherwise.
$ \begin{align} x(n) = u(n) &= \begin{cases} 1 & n\geq 0 \\ 0 & n< 0 \end{cases} \\ \Rightarrow X(e^{j\omega}) &= \frac{1}{1-e^{-j\omega}}+\pi\sum_{k=-\infty}^{\infty}\delta(\omega-2\pi k) \end{align} $

The Delta Function

Recall that in continuous time, the delta function $ \delta(t) $ is not really a function. It might be more accurate to think of it as an operator. In discrete time however, it is much simpler to describe a delta. It is simply a function which equals 1 when $ n=0 $ and 0 everywhere else.
$ \begin{align} x(n) = \delta(n) &= \begin{cases} 1 & n = 0 \\ 0 & n \neq 0 \end{cases} \\ \Rightarrow X(e^{j\omega}) &= 1 \end{align} $

This result makes sense because in the delta function is contains components at every frequency, each of which have the identical amplitude and phase.

Pulse

A pulse of length N that starts at $ N = 0 $ is given by
$ \begin{align} x(n) &= pulse_N(n)\triangleq u(n0 - u(n-N) \\ \Rightarrow X(e^{j\omega}) &= psincN(\omega)e^{-j\omega\frac{N-1}{2}} \end{align} $
where psinc is the periodic sinc function.

A pulse of length 5 is shown in figure 2. Note that the pulse stops after $ n=N-1 = 4 $. You can also think of the pulse as a shifted rect.

figure 2

Periodic Sinc

The psinc or the periodic sinc function is given by
$ psinc_N(\omega) \triangleq \frac{\sin(\omega N/2)}{\sin(\omega/2)} $
The above function is periodic with period $ 2\pi $ when N is odd. It is periodic with period $ 4\pi $ when N is even. You can fix that issue with a phase term.

figure of a periodic sinc

Periodic Rect

The periodic rect or prect function is given by
$ prect_{2\omega_0}(\omega) \triangleq \sum_{k=-\infty}^{\infty}rect(\frac{\omega-2\pi k}{2\omega_0}) $
the $ prect_{2\omega o} $ function has period $ 2\pi $ so it can be a valid DTFT. Each rect has a $ 2\omega_0 $ wide support.

figure of periodic rect

Discrete Space Fourier Transform and Properties

2-D Z-Transform

Relationship between Fourier and Z-Transforms

References

• C. A. Bouman. ECE 637. Class Lecture. Digital Image Processing I. Faculty of Electrical Engineering, Purdue University. Spring 2013.

Questions and comments

If you have any questions, comments, etc. please post them on this page

Back to the "Bouman Lectures on Image Processing" by Maliha Hossain