| Line 19: | Line 19: | ||
'''Answer (74p on Papoulis)''' | '''Answer (74p on Papoulis)''' | ||
| − | A random variable <math>\mathbf{X}</math> is a process of assigning a number <math>\mathbf{X}\left(\xi\right)</math> to every outcome <math>\xi</math> . The result function must satisfy the following two conditions but is otherwise arbitrary: | + | A random variable <math class="inline">\mathbf{X}</math> is a process of assigning a number <math class="inline">\mathbf{X}\left(\xi\right)</math> to every outcome <math class="inline">\xi</math> . The result function must satisfy the following two conditions but is otherwise arbitrary: |
| − | 1. The set <math>\left\{ \mathbf{X}\leq x\right\}</math> is an event for every <math>x</math> . | + | 1. The set <math class="inline">\left\{ \mathbf{X}\leq x\right\}</math> is an event for every <math class="inline">x</math> . |
| − | 2. The probabilities of the events <math>\left\{ \mathbf{X}=\infty\right\}</math> and <math>\left\{ \mathbf{X}=-\infty\right\}</math> equal 0. | + | 2. The probabilities of the events <math class="inline">\left\{ \mathbf{X}=\infty\right\}</math> and <math class="inline">\left\{ \mathbf{X}=-\infty\right\}</math> equal 0. |
'''Answer (Intuitive definition)''' | '''Answer (Intuitive definition)''' | ||
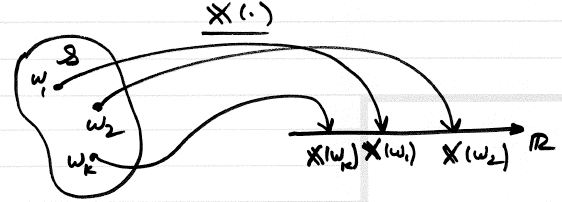
| − | Given <math>\left(\mathcal{S},\mathcal{F},\mathcal{P}\right)</math> , a random variable <math>\mathbf{X}</math> is a mapping from <math>\mathcal{S}</math> to the real line. <math>\mathbf{X}:\mathcal{S}\rightarrow\mathbb{R}</math> . | + | Given <math class="inline">\left(\mathcal{S},\mathcal{F},\mathcal{P}\right)</math> , a random variable <math class="inline">\mathbf{X}</math> is a mapping from <math class="inline">\mathcal{S}</math> to the real line. <math class="inline">\mathbf{X}:\mathcal{S}\rightarrow\mathbb{R}</math> . |
[[Image:pasted40.png]] | [[Image:pasted40.png]] | ||
| Line 41: | Line 41: | ||
'''2. (15% of Total)''' | '''2. (15% of Total)''' | ||
| − | You want to simulate outcomes for an exponential random variable <math>\mathbf{X}</math> with mean <math>1/\lambda</math> . You have a random number generator that produces outcomes for a random variable <math>\mathbf{Y}</math> that is uniformly distributed on the interval <math>\left(0,1\right)</math> . What transformation applied to <math>\mathbf{Y}</math> will yield the desired distribution for <math>\mathbf{X}</math> ? Prove your answer. | + | You want to simulate outcomes for an exponential random variable <math class="inline">\mathbf{X}</math> with mean <math class="inline">1/\lambda</math> . You have a random number generator that produces outcomes for a random variable <math class="inline">\mathbf{Y}</math> that is uniformly distributed on the interval <math class="inline">\left(0,1\right)</math> . What transformation applied to <math class="inline">\mathbf{Y}</math> will yield the desired distribution for <math class="inline">\mathbf{X}</math> ? Prove your answer. |
'''Answer''' | '''Answer''' | ||
| − | <math>f_{\mathbf{X}}\left(x\right)=\lambda e^{-\lambda x}.</math> | + | <math class="inline">f_{\mathbf{X}}\left(x\right)=\lambda e^{-\lambda x}.</math> |
| − | <math>F_{\mathbf{X}}\left(x\right)=1-e^{-\lambda x}.</math> | + | <math class="inline">F_{\mathbf{X}}\left(x\right)=1-e^{-\lambda x}.</math> |
{| | {| | ||
| − | |<math>y=1-e^{-\lambda x}</math> | + | |<math class="inline">y=1-e^{-\lambda x}</math> |
|- | |- | ||
| − | |<math>e^{-\lambda x}=1-y</math> | + | |<math class="inline">e^{-\lambda x}=1-y</math> |
|- | |- | ||
| − | |<math>-\lambda x=\ln\left(1-y\right)</math> | + | |<math class="inline">-\lambda x=\ln\left(1-y\right)</math> |
|- | |- | ||
| − | |<math>x=\frac{-\ln\left(1-y\right)}{\lambda}</math> | + | |<math class="inline">x=\frac{-\ln\left(1-y\right)}{\lambda}</math> |
|- | |- | ||
| − | |<math>x=\frac{-\ln y}{\lambda}.</math> | + | |<math class="inline">x=\frac{-\ln y}{\lambda}.</math> |
|} | |} | ||
| − | <math>\mathbf{X}=F_{\mathbf{X}}^{-1}\left(\mathbf{Y}\right). </math> | + | <math class="inline">\mathbf{X}=F_{\mathbf{X}}^{-1}\left(\mathbf{Y}\right). </math> |
| − | <math>F_{\mathbf{X}}^{-1}\left(y\right)=\frac{-\ln y}{\lambda}.</math> | + | <math class="inline">F_{\mathbf{X}}^{-1}\left(y\right)=\frac{-\ln y}{\lambda}.</math> |
'''3. (20% of Total)''' | '''3. (20% of Total)''' | ||
| − | Consider three independent random variables, <math>\mathbf{X}</math> , <math>\mathbf{Y}</math> , and <math>\mathbf{Z}</math> . Assume that each one is uniformly distributed over the interval <math>\left(0,1\right)</math> . Call “Bin #1” the interval <math>\left(0,\mathbf{X}\right)</math> , and “Bin #2” the interval <math>\left(\mathbf{X},1\right)</math> . | + | Consider three independent random variables, <math class="inline">\mathbf{X}</math> , <math class="inline">\mathbf{Y}</math> , and <math class="inline">\mathbf{Z}</math> . Assume that each one is uniformly distributed over the interval <math class="inline">\left(0,1\right)</math> . Call “Bin #1” the interval <math class="inline">\left(0,\mathbf{X}\right)</math> , and “Bin #2” the interval <math class="inline">\left(\mathbf{X},1\right)</math> . |
'''a. (10%)''' | '''a. (10%)''' | ||
| − | Find the probability that <math>\mathbf{Y}</math> falls into Bin #1 (that is, <math>\mathbf{Y}<\mathbf{X}</math> ). Show your work. | + | Find the probability that <math class="inline">\mathbf{Y}</math> falls into Bin #1 (that is, <math class="inline">\mathbf{Y}<\mathbf{X}</math> ). Show your work. |
'''Solution 1 - Wrong''' | '''Solution 1 - Wrong''' | ||
| − | <math>P\left(\left\{ \mathbf{Y}<\mathbf{X}\right\} \right)=\int_{0}^{1}P\left(\left\{ \mathbf{Y}<k\right\} \cap\left\{ \mathbf{X}\geq k\right\} \right)dk=\int_{0}^{1}P\left(\left\{ \mathbf{Y}<k\right\} \right)\cdot P\left(\left\{ \mathbf{X}\geq k\right\} \right)dk</math><math>=\int_{0}^{1}k\left(1-k\right)dk=\int_{0}^{1}k-k^{2}dk=\frac{1}{2}k^{2}-\frac{1}{3}k^{3}\biggl|_{0}^{1}=\frac{1}{2}-\frac{1}{3}=\frac{1}{6}.</math> | + | <math class="inline">P\left(\left\{ \mathbf{Y}<\mathbf{X}\right\} \right)=\int_{0}^{1}P\left(\left\{ \mathbf{Y}<k\right\} \cap\left\{ \mathbf{X}\geq k\right\} \right)dk=\int_{0}^{1}P\left(\left\{ \mathbf{Y}<k\right\} \right)\cdot P\left(\left\{ \mathbf{X}\geq k\right\} \right)dk</math><math class="inline">=\int_{0}^{1}k\left(1-k\right)dk=\int_{0}^{1}k-k^{2}dk=\frac{1}{2}k^{2}-\frac{1}{3}k^{3}\biggl|_{0}^{1}=\frac{1}{2}-\frac{1}{3}=\frac{1}{6}.</math> |
'''Solution 2''' | '''Solution 2''' | ||
| Line 80: | Line 80: | ||
{| | {| | ||
| − | |<math>\int_{0}^{1}\int_{0}^{1}cdxdy=1</math> | + | |<math class="inline">\int_{0}^{1}\int_{0}^{1}cdxdy=1</math> |
|- | |- | ||
| − | |<math>\int_{0}^{1}cdy=1</math> | + | |<math class="inline">\int_{0}^{1}cdy=1</math> |
|- | |- | ||
| − | |<math>c=1</math> | + | |<math class="inline">c=1</math> |
|} | |} | ||
| − | <math>P\left(\left\{ \mathbf{Y}<\mathbf{X}\right\} \right)=\int_{0}^{1}\int_{0}^{x}1dydx=\int_{0}^{1}xdx=\frac{x^{2}}{2}\biggl|_{0}^{1}=\frac{1}{2}.</math> | + | <math class="inline">P\left(\left\{ \mathbf{Y}<\mathbf{X}\right\} \right)=\int_{0}^{1}\int_{0}^{x}1dydx=\int_{0}^{1}xdx=\frac{x^{2}}{2}\biggl|_{0}^{1}=\frac{1}{2}.</math> |
'''b. (10%)''' | '''b. (10%)''' | ||
| − | Find the probability that both <math>\mathbf{Y}</math> and <math>\mathbf{Z}</math> fall into Bin #1. Show your work. | + | Find the probability that both <math class="inline">\mathbf{Y}</math> and <math class="inline">\mathbf{Z}</math> fall into Bin #1. Show your work. |
| − | <math>P\left(\left\{ \mathbf{Y}<\mathbf{X}\right\} \cap\left\{ \mathbf{Z}<\mathbf{X}\right\} \right)=\int_{0}^{1}\int_{0}^{x}\int_{0}^{x}1dzdydx=\int_{0}^{1}\int_{0}^{x}xdydx=\int_{0}^{1}x^{2}dx=\frac{1}{3}.</math> | + | <math class="inline">P\left(\left\{ \mathbf{Y}<\mathbf{X}\right\} \cap\left\{ \mathbf{Z}<\mathbf{X}\right\} \right)=\int_{0}^{1}\int_{0}^{x}\int_{0}^{x}1dzdydx=\int_{0}^{1}\int_{0}^{x}xdydx=\int_{0}^{1}x^{2}dx=\frac{1}{3}.</math> |
'''4. (25% of Total)''' | '''4. (25% of Total)''' | ||
| − | Let <math>\mathbf{X}_{n},\; n=1,2,\cdots</math> , be a zero mean, discrete-time, white noise process with <math>E\left(\mathbf{X}_{n}^{2}\right)=1</math> for all <math>n</math> . Let <math>\mathbf{Y}_{0}</math> be a random variable that is independent of the sequence <math>\left\{ \mathbf{X}_{n}\right\}</math> , has mean <math>0</math> , and has variance <math>\sigma^{2}</math> . Define <math>\mathbf{Y}_{n},\; n=1,2,\cdots</math> , to be an autoregressive process as follows: <math>\mathbf{Y}_{n}=\frac{1}{3}\mathbf{Y}_{n-1}+\mathbf{X}_{n}.</math> | + | Let <math class="inline">\mathbf{X}_{n},\; n=1,2,\cdots</math> , be a zero mean, discrete-time, white noise process with <math class="inline">E\left(\mathbf{X}_{n}^{2}\right)=1</math> for all <math class="inline">n</math> . Let <math class="inline">\mathbf{Y}_{0}</math> be a random variable that is independent of the sequence <math class="inline">\left\{ \mathbf{X}_{n}\right\}</math> , has mean <math class="inline">0</math> , and has variance <math class="inline">\sigma^{2}</math> . Define <math class="inline">\mathbf{Y}_{n},\; n=1,2,\cdots</math> , to be an autoregressive process as follows: <math class="inline">\mathbf{Y}_{n}=\frac{1}{3}\mathbf{Y}_{n-1}+\mathbf{X}_{n}.</math> |
'''a. (20 %)''' | '''a. (20 %)''' | ||
| − | Show that <math>\mathbf{Y}_{n}</math> is asymptotically wide sense stationary and find its steady state mean and autocorrelation function. | + | Show that <math class="inline">\mathbf{Y}_{n}</math> is asymptotically wide sense stationary and find its steady state mean and autocorrelation function. |
| − | <math>\mathbf{Y}_{n}=\frac{1}{3}\mathbf{Y}_{n-1}+\mathbf{X}_{n}=\frac{1}{3}\left(\frac{1}{3}\mathbf{Y}_{n-2}+\mathbf{X}_{n-1}\right)+\mathbf{X}_{n}=\left(\frac{1}{3}\right)^{2}\mathbf{Y}_{n-2}+\mathbf{X}_{n}+\frac{1}{3}\mathbf{X}_{n-1}</math><math>=\cdots=\left(\frac{1}{3}\right)^{n}\mathbf{Y}_{0}+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}.</math> | + | <math class="inline">\mathbf{Y}_{n}=\frac{1}{3}\mathbf{Y}_{n-1}+\mathbf{X}_{n}=\frac{1}{3}\left(\frac{1}{3}\mathbf{Y}_{n-2}+\mathbf{X}_{n-1}\right)+\mathbf{X}_{n}=\left(\frac{1}{3}\right)^{2}\mathbf{Y}_{n-2}+\mathbf{X}_{n}+\frac{1}{3}\mathbf{X}_{n-1}</math><math class="inline">=\cdots=\left(\frac{1}{3}\right)^{n}\mathbf{Y}_{0}+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}.</math> |
| − | <math>E\left[\mathbf{Y}_{n}\right]=E\left[\left(\frac{1}{3}\right)^{n}\mathbf{Y}_{0}+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}\right]=\left(\frac{1}{3}\right)^{n}E\left[\mathbf{Y}_{0}\right]+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}E\left[\mathbf{X}_{n-k}\right]</math><math>=\left(\frac{1}{3}\right)^{n}\cdot0+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\cdot0=0.</math> | + | <math class="inline">E\left[\mathbf{Y}_{n}\right]=E\left[\left(\frac{1}{3}\right)^{n}\mathbf{Y}_{0}+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}\right]=\left(\frac{1}{3}\right)^{n}E\left[\mathbf{Y}_{0}\right]+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}E\left[\mathbf{X}_{n-k}\right]</math><math class="inline">=\left(\frac{1}{3}\right)^{n}\cdot0+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\cdot0=0.</math> |
| − | <math>E\left[\mathbf{Y}_{m}\mathbf{Y}_{n}\right]=\left(\frac{1}{3}\right)^{m+n}E\left[\mathbf{Y}_{0}^{2}\right]+\left(\frac{1}{3}\right)^{m}E\left[\mathbf{Y}_{0}\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}\right]</math><math>\qquad+\left(\frac{1}{3}\right)^{n}E\left[\mathbf{Y}_{0}\sum_{k=0}^{m-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}\right]+\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}\left(\frac{1}{3}\right)^{i+j}E\left[\mathbf{X}_{m-i}\cdot\mathbf{X}_{n-j}\right]</math><math>=\left(\frac{1}{3}\right)^{m+n}\cdot\left(\sigma^{2}+0^{2}\right)+\sum_{k=1}^{\min\left(m,n\right)}\left(\frac{1}{3}\right)^{m+n-2k}</math><math>=\left(\frac{1}{3}\right)^{m+n}\cdot\sigma^{2}+\sum_{k=1}^{\min\left(m,n\right)}\left(\frac{1}{3}\right)^{m+n-2k}.</math> | + | <math class="inline">E\left[\mathbf{Y}_{m}\mathbf{Y}_{n}\right]=\left(\frac{1}{3}\right)^{m+n}E\left[\mathbf{Y}_{0}^{2}\right]+\left(\frac{1}{3}\right)^{m}E\left[\mathbf{Y}_{0}\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}\right]</math><math class="inline">\qquad+\left(\frac{1}{3}\right)^{n}E\left[\mathbf{Y}_{0}\sum_{k=0}^{m-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}\right]+\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}\left(\frac{1}{3}\right)^{i+j}E\left[\mathbf{X}_{m-i}\cdot\mathbf{X}_{n-j}\right]</math><math class="inline">=\left(\frac{1}{3}\right)^{m+n}\cdot\left(\sigma^{2}+0^{2}\right)+\sum_{k=1}^{\min\left(m,n\right)}\left(\frac{1}{3}\right)^{m+n-2k}</math><math class="inline">=\left(\frac{1}{3}\right)^{m+n}\cdot\sigma^{2}+\sum_{k=1}^{\min\left(m,n\right)}\left(\frac{1}{3}\right)^{m+n-2k}.</math> |
| − | <math>\because\;\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}\left(\frac{1}{3}\right)^{i+j}E\left[\mathbf{X}_{m-i}\cdot\mathbf{X}_{n-j}\right]=\sum_{i=1}^{m}\sum_{j=1}^{n}\left(\frac{1}{3}\right)^{m-i}\left(\frac{1}{3}\right)^{n-j}E\left[\mathbf{X}_{i}\cdot\mathbf{X}_{j}\right]=\sum_{k=1}^{\min\left(m,n\right)}\left(\frac{1}{3}\right)^{m+n-2k}.</math> | + | <math class="inline">\because\;\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}\left(\frac{1}{3}\right)^{i+j}E\left[\mathbf{X}_{m-i}\cdot\mathbf{X}_{n-j}\right]=\sum_{i=1}^{m}\sum_{j=1}^{n}\left(\frac{1}{3}\right)^{m-i}\left(\frac{1}{3}\right)^{n-j}E\left[\mathbf{X}_{i}\cdot\mathbf{X}_{j}\right]=\sum_{k=1}^{\min\left(m,n\right)}\left(\frac{1}{3}\right)^{m+n-2k}.</math> |
'''b. (5%)''' | '''b. (5%)''' | ||
| − | For what choice of <math>\sigma^{2}</math> is the process wide sense stationary; i.e., not just asymptotically wide sense stationary? | + | For what choice of <math class="inline">\sigma^{2}</math> is the process wide sense stationary; i.e., not just asymptotically wide sense stationary? |
'''5. (25% of Total)''' | '''5. (25% of Total)''' | ||
| − | Suppose that “sensor nodes” are spread around the ground (two-dimensional space) according to a Poisson Process, with an average density of nodes per unit area of <math>\lambda</math> . We are interested in the number and location of nodes inside a circle <math>C</math> of radius one that is centered at the origin. You must quote, but do not have to prove, properties of the Poisson process that you use in your solutions to the following questions: | + | Suppose that “sensor nodes” are spread around the ground (two-dimensional space) according to a Poisson Process, with an average density of nodes per unit area of <math class="inline">\lambda</math> . We are interested in the number and location of nodes inside a circle <math class="inline">C</math> of radius one that is centered at the origin. You must quote, but do not have to prove, properties of the Poisson process that you use in your solutions to the following questions: |
'''a. (10%)''' | '''a. (10%)''' | ||
| − | Given that a node is in the circle C , determine the density or distribution function of its distance <math>\mathbf{D}</math> from the origin. | + | Given that a node is in the circle C , determine the density or distribution function of its distance <math class="inline">\mathbf{D}</math> from the origin. |
| − | • <math>i)\; d<0,\; F_{\mathbf{D}}\left(d\right)=0.</math> | + | • <math class="inline">i)\; d<0,\; F_{\mathbf{D}}\left(d\right)=0.</math> |
| − | • <math>ii)\;0\leq d\leq1,\; F_{\mathbf{D}}\left(d\right)=P\left(\left\{ \mathbf{D}\leq d\right\} \right)=\frac{d^{2}\pi}{1^{2}\pi}=d^{2}.</math> | + | • <math class="inline">ii)\;0\leq d\leq1,\; F_{\mathbf{D}}\left(d\right)=P\left(\left\{ \mathbf{D}\leq d\right\} \right)=\frac{d^{2}\pi}{1^{2}\pi}=d^{2}.</math> |
| − | • <math>iii)\;1<d,\; F_{\mathbf{D}}\left(d\right)=1.</math> | + | • <math class="inline">iii)\;1<d,\; F_{\mathbf{D}}\left(d\right)=1.</math> |
| − | <math>\therefore\; F_{\mathbf{D}}\left(d\right)=\begin{cases} | + | <math class="inline">\therefore\; F_{\mathbf{D}}\left(d\right)=\begin{cases} |
\begin{array}{lll} | \begin{array}{lll} | ||
0 & & ,\; d<0\\ | 0 & & ,\; d<0\\ | ||
| Line 136: | Line 136: | ||
\end{array}\end{cases}</math> | \end{array}\end{cases}</math> | ||
| − | <math>f_{\mathbf{D}}\left(d\right)=2d\cdot\mathbf{1}_{\left[0,1\right]}\left(d\right).</math> | + | <math class="inline">f_{\mathbf{D}}\left(d\right)=2d\cdot\mathbf{1}_{\left[0,1\right]}\left(d\right).</math> |
'''b. (15%)''' | '''b. (15%)''' | ||
| − | Find the density or distribution of the distance from the center of <math>C</math> to the node inside <math>C</math> that is closest to the origin. | + | Find the density or distribution of the distance from the center of <math class="inline">C</math> to the node inside <math class="inline">C</math> that is closest to the origin. |
| − | <math>\mathbf{X}</math> : the random variable for the distance from the center of <math>C</math> to the node inside <math>C</math> that is closest to the origin | + | <math class="inline">\mathbf{X}</math> : the random variable for the distance from the center of <math class="inline">C</math> to the node inside <math class="inline">C</math> that is closest to the origin |
| − | <math>F_{\mathbf{X}}\left(x\right)=P\left(\left\{ \mathbf{X}\leq x\right\} \right)=1-P\left(\left\{ \mathbf{X}>x\right\} \right)</math><math>=1-P\left(\left\{ \textnormal{no sensor nodes in the circle that has a radius }x\right\} \right)</math><math>=1-e^{-\lambda x^{2}\pi}.</math> | + | <math class="inline">F_{\mathbf{X}}\left(x\right)=P\left(\left\{ \mathbf{X}\leq x\right\} \right)=1-P\left(\left\{ \mathbf{X}>x\right\} \right)</math><math class="inline">=1-P\left(\left\{ \textnormal{no sensor nodes in the circle that has a radius }x\right\} \right)</math><math class="inline">=1-e^{-\lambda x^{2}\pi}.</math> |
| − | <math>f_{\mathbf{X}}\left(x\right)=\frac{d}{dx}F_{\mathbf{X}}\left(x\right)=2\lambda x\pi\cdot e^{-\lambda x^{2}\pi}.</math> | + | <math class="inline">f_{\mathbf{X}}\left(x\right)=\frac{d}{dx}F_{\mathbf{X}}\left(x\right)=2\lambda x\pi\cdot e^{-\lambda x^{2}\pi}.</math> |
---- | ---- | ||
Revision as of 07:27, 1 December 2010
7.7 QE 2003 August
1. (15% of Total)
This question is a set of short-answer questions (no proofs):
(a) (5%)
State the definition of a Probability Space.
Answer
You can see the definition of a Probability Space.
(b) (5%)
State the definition of a random variable; use notation from your answer in part (a).
Answer (74p on Papoulis)
A random variable $ \mathbf{X} $ is a process of assigning a number $ \mathbf{X}\left(\xi\right) $ to every outcome $ \xi $ . The result function must satisfy the following two conditions but is otherwise arbitrary:
1. The set $ \left\{ \mathbf{X}\leq x\right\} $ is an event for every $ x $ .
2. The probabilities of the events $ \left\{ \mathbf{X}=\infty\right\} $ and $ \left\{ \mathbf{X}=-\infty\right\} $ equal 0.
Answer (Intuitive definition)
Given $ \left(\mathcal{S},\mathcal{F},\mathcal{P}\right) $ , a random variable $ \mathbf{X} $ is a mapping from $ \mathcal{S} $ to the real line. $ \mathbf{X}:\mathcal{S}\rightarrow\mathbb{R} $ .
(c) (5%)
State the Strong Law of Large Numbers.
Answer
You can see the definition of the Strong Law of Large Numbers.
2. (15% of Total)
You want to simulate outcomes for an exponential random variable $ \mathbf{X} $ with mean $ 1/\lambda $ . You have a random number generator that produces outcomes for a random variable $ \mathbf{Y} $ that is uniformly distributed on the interval $ \left(0,1\right) $ . What transformation applied to $ \mathbf{Y} $ will yield the desired distribution for $ \mathbf{X} $ ? Prove your answer.
Answer
$ f_{\mathbf{X}}\left(x\right)=\lambda e^{-\lambda x}. $
$ F_{\mathbf{X}}\left(x\right)=1-e^{-\lambda x}. $
| $ y=1-e^{-\lambda x} $ |
| $ e^{-\lambda x}=1-y $ |
| $ -\lambda x=\ln\left(1-y\right) $ |
| $ x=\frac{-\ln\left(1-y\right)}{\lambda} $ |
| $ x=\frac{-\ln y}{\lambda}. $ |
$ \mathbf{X}=F_{\mathbf{X}}^{-1}\left(\mathbf{Y}\right). $
$ F_{\mathbf{X}}^{-1}\left(y\right)=\frac{-\ln y}{\lambda}. $
3. (20% of Total)
Consider three independent random variables, $ \mathbf{X} $ , $ \mathbf{Y} $ , and $ \mathbf{Z} $ . Assume that each one is uniformly distributed over the interval $ \left(0,1\right) $ . Call “Bin #1” the interval $ \left(0,\mathbf{X}\right) $ , and “Bin #2” the interval $ \left(\mathbf{X},1\right) $ .
a. (10%)
Find the probability that $ \mathbf{Y} $ falls into Bin #1 (that is, $ \mathbf{Y}<\mathbf{X} $ ). Show your work.
Solution 1 - Wrong
$ P\left(\left\{ \mathbf{Y}<\mathbf{X}\right\} \right)=\int_{0}^{1}P\left(\left\{ \mathbf{Y}<k\right\} \cap\left\{ \mathbf{X}\geq k\right\} \right)dk=\int_{0}^{1}P\left(\left\{ \mathbf{Y}<k\right\} \right)\cdot P\left(\left\{ \mathbf{X}\geq k\right\} \right)dk $$ =\int_{0}^{1}k\left(1-k\right)dk=\int_{0}^{1}k-k^{2}dk=\frac{1}{2}k^{2}-\frac{1}{3}k^{3}\biggl|_{0}^{1}=\frac{1}{2}-\frac{1}{3}=\frac{1}{6}. $
Solution 2
| $ \int_{0}^{1}\int_{0}^{1}cdxdy=1 $ |
| $ \int_{0}^{1}cdy=1 $ |
| $ c=1 $ |
$ P\left(\left\{ \mathbf{Y}<\mathbf{X}\right\} \right)=\int_{0}^{1}\int_{0}^{x}1dydx=\int_{0}^{1}xdx=\frac{x^{2}}{2}\biggl|_{0}^{1}=\frac{1}{2}. $
b. (10%)
Find the probability that both $ \mathbf{Y} $ and $ \mathbf{Z} $ fall into Bin #1. Show your work.
$ P\left(\left\{ \mathbf{Y}<\mathbf{X}\right\} \cap\left\{ \mathbf{Z}<\mathbf{X}\right\} \right)=\int_{0}^{1}\int_{0}^{x}\int_{0}^{x}1dzdydx=\int_{0}^{1}\int_{0}^{x}xdydx=\int_{0}^{1}x^{2}dx=\frac{1}{3}. $
4. (25% of Total)
Let $ \mathbf{X}_{n},\; n=1,2,\cdots $ , be a zero mean, discrete-time, white noise process with $ E\left(\mathbf{X}_{n}^{2}\right)=1 $ for all $ n $ . Let $ \mathbf{Y}_{0} $ be a random variable that is independent of the sequence $ \left\{ \mathbf{X}_{n}\right\} $ , has mean $ 0 $ , and has variance $ \sigma^{2} $ . Define $ \mathbf{Y}_{n},\; n=1,2,\cdots $ , to be an autoregressive process as follows: $ \mathbf{Y}_{n}=\frac{1}{3}\mathbf{Y}_{n-1}+\mathbf{X}_{n}. $
a. (20 %)
Show that $ \mathbf{Y}_{n} $ is asymptotically wide sense stationary and find its steady state mean and autocorrelation function.
$ \mathbf{Y}_{n}=\frac{1}{3}\mathbf{Y}_{n-1}+\mathbf{X}_{n}=\frac{1}{3}\left(\frac{1}{3}\mathbf{Y}_{n-2}+\mathbf{X}_{n-1}\right)+\mathbf{X}_{n}=\left(\frac{1}{3}\right)^{2}\mathbf{Y}_{n-2}+\mathbf{X}_{n}+\frac{1}{3}\mathbf{X}_{n-1} $$ =\cdots=\left(\frac{1}{3}\right)^{n}\mathbf{Y}_{0}+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}. $
$ E\left[\mathbf{Y}_{n}\right]=E\left[\left(\frac{1}{3}\right)^{n}\mathbf{Y}_{0}+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}\right]=\left(\frac{1}{3}\right)^{n}E\left[\mathbf{Y}_{0}\right]+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}E\left[\mathbf{X}_{n-k}\right] $$ =\left(\frac{1}{3}\right)^{n}\cdot0+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\cdot0=0. $
$ E\left[\mathbf{Y}_{m}\mathbf{Y}_{n}\right]=\left(\frac{1}{3}\right)^{m+n}E\left[\mathbf{Y}_{0}^{2}\right]+\left(\frac{1}{3}\right)^{m}E\left[\mathbf{Y}_{0}\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}\right] $$ \qquad+\left(\frac{1}{3}\right)^{n}E\left[\mathbf{Y}_{0}\sum_{k=0}^{m-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}\right]+\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}\left(\frac{1}{3}\right)^{i+j}E\left[\mathbf{X}_{m-i}\cdot\mathbf{X}_{n-j}\right] $$ =\left(\frac{1}{3}\right)^{m+n}\cdot\left(\sigma^{2}+0^{2}\right)+\sum_{k=1}^{\min\left(m,n\right)}\left(\frac{1}{3}\right)^{m+n-2k} $$ =\left(\frac{1}{3}\right)^{m+n}\cdot\sigma^{2}+\sum_{k=1}^{\min\left(m,n\right)}\left(\frac{1}{3}\right)^{m+n-2k}. $
$ \because\;\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}\left(\frac{1}{3}\right)^{i+j}E\left[\mathbf{X}_{m-i}\cdot\mathbf{X}_{n-j}\right]=\sum_{i=1}^{m}\sum_{j=1}^{n}\left(\frac{1}{3}\right)^{m-i}\left(\frac{1}{3}\right)^{n-j}E\left[\mathbf{X}_{i}\cdot\mathbf{X}_{j}\right]=\sum_{k=1}^{\min\left(m,n\right)}\left(\frac{1}{3}\right)^{m+n-2k}. $
b. (5%)
For what choice of $ \sigma^{2} $ is the process wide sense stationary; i.e., not just asymptotically wide sense stationary?
5. (25% of Total)
Suppose that “sensor nodes” are spread around the ground (two-dimensional space) according to a Poisson Process, with an average density of nodes per unit area of $ \lambda $ . We are interested in the number and location of nodes inside a circle $ C $ of radius one that is centered at the origin. You must quote, but do not have to prove, properties of the Poisson process that you use in your solutions to the following questions:
a. (10%)
Given that a node is in the circle C , determine the density or distribution function of its distance $ \mathbf{D} $ from the origin.
• $ i)\; d<0,\; F_{\mathbf{D}}\left(d\right)=0. $
• $ ii)\;0\leq d\leq1,\; F_{\mathbf{D}}\left(d\right)=P\left(\left\{ \mathbf{D}\leq d\right\} \right)=\frac{d^{2}\pi}{1^{2}\pi}=d^{2}. $
• $ iii)\;1<d,\; F_{\mathbf{D}}\left(d\right)=1. $
$ \therefore\; F_{\mathbf{D}}\left(d\right)=\begin{cases} \begin{array}{lll} 0 & & ,\; d<0\\ d^{2} & & ,\;0\leq d\leq1\\ 1 & & ,\;1<d \end{array}\end{cases} $
$ f_{\mathbf{D}}\left(d\right)=2d\cdot\mathbf{1}_{\left[0,1\right]}\left(d\right). $
b. (15%)
Find the density or distribution of the distance from the center of $ C $ to the node inside $ C $ that is closest to the origin.
$ \mathbf{X} $ : the random variable for the distance from the center of $ C $ to the node inside $ C $ that is closest to the origin
$ F_{\mathbf{X}}\left(x\right)=P\left(\left\{ \mathbf{X}\leq x\right\} \right)=1-P\left(\left\{ \mathbf{X}>x\right\} \right) $$ =1-P\left(\left\{ \textnormal{no sensor nodes in the circle that has a radius }x\right\} \right) $$ =1-e^{-\lambda x^{2}\pi}. $
$ f_{\mathbf{X}}\left(x\right)=\frac{d}{dx}F_{\mathbf{X}}\left(x\right)=2\lambda x\pi\cdot e^{-\lambda x^{2}\pi}. $