Line 60: Line 60:
 
'''Case 2''': X continuous, Y discrete <br/>
 
'''Case 2''': X continuous, Y discrete <br/>
 
The pmf of Y in this case is <br/>
 
The pmf of Y in this case is <br/>
−
<center>p<math>_Y</math>(y) = P(g(X)=y) = P(X ∈ D</math>_Y</math>) =</center><br/>
+
<center>p<math>_Y</math>(y) = P(g(X)=y) = P(X ∈ D<math>_Y</math>) =</center><br/>
 
<center>where D<math>_Y</math> ≡ {x ∈ '''R''': g(x)=y} ∀y ∈ ''R''<math>_Y</math></center>
 
<center>where D<math>_Y</math> ≡ {x ∈ '''R''': g(x)=y} ∀y ∈ ''R''<math>_Y</math></center>
 +
 +
Then, <br/>
 +
<center><math> p_Y(y) = \int_{D_y}f)X(x)dx</math></center>
 +
 +
'''Example''' Let g(x) = u(x - x<math>_0</math>) for some x<math>_0</math> ∈ '''R''', and let Y=g(X). Then <math>R_Y</math> = {0,1} and <br/>
 +
<center> D<math>_0</math> = {x ∈ '''R''': x < x<math>_0</math>} = (-∞, x<math>_0</math>)</center>
 +
<center> D<math>_1</math> = {x ∈ '''R''': x ≥ x<math>_0</math>} = [ x<math>_0</math>, ∞)</center>
 +
So, <br/>
 +
<center><math> p_Y(y) = \begin{cases}
 +
\int_{-\infty}^{x_0} f_X(x)dx & y=0\\
 +
\\
 +
\int_{x_0}^{-\infty} f_X(x)dx & y=1
 +
\end{cases}</math></center>
 +
 +
 +
'''Case 3:''' X and Y continuous <br/>
 +
 +
We will discuss 2 methods for finding f<math>_Y</math> in this case.
 +
 +
'''Approach 1'''<br/>
 +
First, find the cdf F<math>_Y</math>. <br/>
 +
<center>F<math>_Y</math>(y) = P(g(X) ≤ y) = P(X ∈ D<math>_y</math>) <br/>
 +
where D<math>_y</math> = {x ∈ '''R''': g(x) ≤ y}.</center>
 +
Then <br/>
 +
<center><math>F_Y(f) = \int_{D_y}f_X(x)dx</math></center>
 +
 +
Differentiate F<math>_Y</math> to get f<math>_y</math>.
 +
 +
You can find D<math>_Y</math> graphically or analytically
 +
 +
 +
'''Example'''
 +
 +
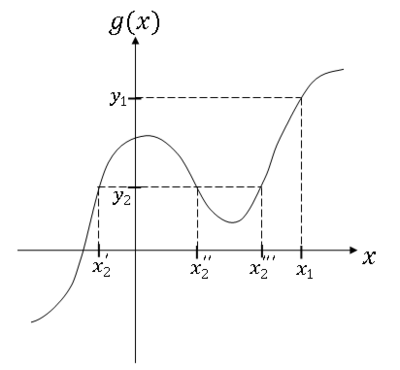
<center>[[Image:fig2_functions_on_rv.png|400px|thumb|left|Fig 2: This plot of g(x) can be used to derive D</math>_Y</math> graphically]]</center>
 +
 +
 +
For y = y<math>_1</math> and y = y<math>_2</math>, <br/>
 +
<center><math>\begin{align}
 +
D_{y_1} &= \{x:\;x \leq x_1\} \\
 +
D_{y_2} &= \{x:\;x\leq x_2'\} \cup \{x:\;x_2''<x\leq x_2'''\}
 +
\end{align}</math></center>
 +
 +
Then <br/>
 +
<center><math>\begin{align}
 +
F_Y(y_1) &= \int_{-\infty}^{x_1}f_X(x)dx \\
 +
\\
 +
F_Y(y_2) &= \int_{-\infty}^{x_2'}f_X(x)dx + \int_{x_2''}^{x_2'''}f_X(x)dx
 +
\end{align}</math></center>
 +
 +
 +
'''Example''' Y = aX + b, a,b ∈ '''R''', a ≠ 0<br/>
 +
<center>F<math>_Y</math>(y) = P(aX + b ≤ y)</center>
 +
So, <br/>
 +
<center><math>\begin{align}
 +
D_y&=\{x\in\mathbb R: x\leq\frac{y-b}{a}\}\quad\mbox{if}\;a>0 \\
 +
D_y&=\{x\in\mathbb R: x\geq\frac{y-b}{a}\}\quad\mbox{if}\;a<0
 +
\end{align}</math></center>
 +
Then <br/>
 +
<center><math>F_Y(y)=\begin{cases}
 +
\int_{-\infty}^{\frac{y-b}{a}}f_X(x)dx & \mbox{if }\;a>0 \\
 +
\\
 +
\int_{\frac{y-b}{a}}^{-\infty}f_X(x)dx & \mbox{if }\;a<0
 +
\end{cases}</math></center>
 +
 +
 +
'''Example''' Y = X<math>^2</math> <br/>
 +
 +
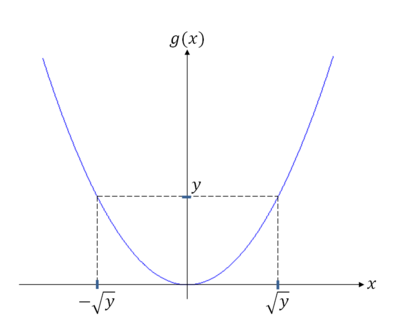
<center>[[Image:fig3_functions_on_rv.png|400px|thumb|left|Fig 3: y = x<math>^2</math>]]</center>
 +
 +
 +
For y < 0, D<math>_y</math> = ø <br/>
 +
For y ≥ 0, <br/>
 +
<center><math>\begin{align}
 +
F_Y(y) &= P(X^2\leq y) \\
 +
&= P(-\sqrt{y} <X\leq \sqrt{y})
 +
\end{align}</math></center>
 +
So, <br/>
 +
<center><math> D_y = (-\sqrt{y},\sqrt{y})</math></center>
 +
and <br/>
 +
<center><math>F_Y(y) = \int_{-\sqrt{y}}^{\sqrt{y}}f_X(x)dx</math></center>

Revision as of 10:03, 13 October 2013


Random Variables and Signals

Topic 8: Functions of Random Variables



We often do not work with the random variable we observe directly, but with some function of that random variable. So, instead of working with a random variable X, we might instead have some random variable Y=g(X) for some function g:R → R.
In this case, we might model Y directly to bet f$ _Y $(y), especially if we do not know g. Or we might have a model for X and find f$ _Y $(y) (or p$ _Y $(y)) as a function of f$ _X $ (or p$ _X $ and g.
We will discuss the latter approach here.

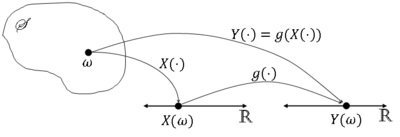
More formally, let X be a random variable on (S,F,P) and consider a mapping g:R → R. Then let Y$ (\omega)= $g(X($ \omega)) $ ∀$ \omega $ ∈ S.
We normally write this as Y=g(X).

Graphically,

Fig 1: Mapping from S to X to Y under g


Is Y a random variable? We must have Y$ ^{-1} $(A) ≡ {$ \omega $ ∈ S: Y$ (\omega) $ ∈ A} = {$ \omega $ ∈ S: g(X$ (\omega) $) ∈ A} be an element of F ∀A ∈ B(R) (Y must be Borel measurable).
We will only consider functions g in this class for which Y$ ^{-1} $(A) ∈ F ∀A ∈ B(R), so that if Y=g(X) for some random variable X, Y will be a random variable.

What is the distribution of Y? Consider 3 cases:

  1. X discrete, Y discrete
  2. X continuous, Y discrete
  3. X continuous, Y continuous

Note: you cannot have a continuous Y from a discrete X.

Case 1: X & Y discrete
Let $ R_X $≡ X(S) be the range space of X and math>R_Y</math>≡ g(X(S)) be the range space of Y. Then the pmf of Y is

p$ _Y $(y) = P(Y=y) = P(g(X)=y)

But this means that

$ p_Y(y) = \sum_{x\in\mathcal{R}_X:g(x)=y}p_X(x)\;\;\forall y\in\mathcal{R}_Y $


Example $ \quad $ Let X be the value rolled on a die and

$ Y = \begin{cases} 1 & \mbox{if}\;X\;\mbox{is odd} \\ 0 & \mbox{if}\;X\;\mbox{is even} \end{cases} $

Then R$ _X $ = {0,1,2,3,4,5,6} and R$ _Y $ = {0,1} and g(x) = x % 2.

Now
$ p_Y(y) = \sum_{x\in\mathcal{R}_X:g(x)=y}p_X(x) $
$ \begin{align} \Rightarrow p_Y(0) &= p_X(2)+p_X(4)+p_X(6) \\ p_Y(1) &= p_X(1)+p_X(3)+p_X(5) \end{align} $


Case 2: X continuous, Y discrete
The pmf of Y in this case is

p$ _Y $(y) = P(g(X)=y) = P(X ∈ D$ _Y $) =

where D$ _Y $ ≡ {x ∈ R: g(x)=y} ∀y ∈ R$ _Y $

Then,

$ p_Y(y) = \int_{D_y}f)X(x)dx $

Example Let g(x) = u(x - x$ _0 $) for some x$ _0 $ ∈ R, and let Y=g(X). Then $ R_Y $ = {0,1} and

D$ _0 $ = {x ∈ R: x < x$ _0 $} = (-∞, x$ _0 $)
D$ _1 $ = {x ∈ R: x ≥ x$ _0 $} = [ x$ _0 $, ∞)

So,

$ p_Y(y) = \begin{cases} \int_{-\infty}^{x_0} f_X(x)dx & y=0\\ \\ \int_{x_0}^{-\infty} f_X(x)dx & y=1 \end{cases} $


Case 3: X and Y continuous

We will discuss 2 methods for finding f$ _Y $ in this case.

Approach 1
First, find the cdf F$ _Y $.

F$ _Y $(y) = P(g(X) ≤ y) = P(X ∈ D$ _y $)
where D$ _y $ = {x ∈ R: g(x) ≤ y}.

Then

$ F_Y(f) = \int_{D_y}f_X(x)dx $

Differentiate F$ _Y $ to get f$ _y $.

You can find D$ _Y $ graphically or analytically


Example

Fig 2: This plot of g(x) can be used to derive D</math>_Y</math> graphically


For y = y$ _1 $ and y = y$ _2 $,

$ \begin{align} D_{y_1} &= \{x:\;x \leq x_1\} \\ D_{y_2} &= \{x:\;x\leq x_2'\} \cup \{x:\;x_2''<x\leq x_2'''\} \end{align} $

Then

$ \begin{align} F_Y(y_1) &= \int_{-\infty}^{x_1}f_X(x)dx \\ \\ F_Y(y_2) &= \int_{-\infty}^{x_2'}f_X(x)dx + \int_{x_2''}^{x_2'''}f_X(x)dx \end{align} $


Example Y = aX + b, a,b ∈ R, a ≠ 0

F$ _Y $(y) = P(aX + b ≤ y)

So,

$ \begin{align} D_y&=\{x\in\mathbb R: x\leq\frac{y-b}{a}\}\quad\mbox{if}\;a>0 \\ D_y&=\{x\in\mathbb R: x\geq\frac{y-b}{a}\}\quad\mbox{if}\;a<0 \end{align} $

Then

$ F_Y(y)=\begin{cases} \int_{-\infty}^{\frac{y-b}{a}}f_X(x)dx & \mbox{if }\;a>0 \\ \\ \int_{\frac{y-b}{a}}^{-\infty}f_X(x)dx & \mbox{if }\;a<0 \end{cases} $


Example Y = X$ ^2 $

Fig 3: y = x$ ^2 $


For y < 0, D$ _y $ = ø
For y ≥ 0,

$ \begin{align} F_Y(y) &= P(X^2\leq y) \\ &= P(-\sqrt{y} <X\leq \sqrt{y}) \end{align} $

So,

$ D_y = (-\sqrt{y},\sqrt{y}) $

and

$ F_Y(y) = \int_{-\sqrt{y}}^{\sqrt{y}}f_X(x)dx $
Retrieved from "https://www.projectrhea.org/rhea/index.php?title=ECE600_F13_rv_Functions_of_random_variable_mhossain&oldid=59268"
Shortcuts
Help Main Wiki Page Random Page Special Pages Log in
Search

Alumni Liaison

Followed her dream after having raised her family.

Ruth Enoch, PhD Mathematics