(New page: Category:ECE600 Category:Lecture notes Back to all ECE 600 notes <center><font size= 4> '''Random Variables and Signals''' </font size> <font size=...) |
|||
| Line 8: | Line 8: | ||
</font size> | </font size> | ||
| − | <font size= 3> Topic 18: | + | <font size= 3> Topic 18: Stochastic Convergence</font size> |
</center> | </center> | ||
---- | ---- | ||
| + | |||
| + | ==Stochastic Convergence== | ||
| + | |||
| + | We will now consider infinite sequences of random variables. We will discuss what it means for such a sequence to converge. This will lead to some very important results: the laws of large numbers and the Central Limit Theorem. | ||
| + | |||
| + | Consider a sequence X<math>_1</math>,X<math>_2</math>,..., where each X<math>_i</math> is a random variable on (''S,F,''P). We will call this a random sequence (or a discrete-time random process). | ||
| + | |||
| + | '''Notation''' <math>\qquad</math> X<math>_n</math> may refer to either the sequence itself or to the nth element in the sequence. We may also use {X<math>_n</math>} to denote the sequence, or X<math>_n</math>, n ≥ 1. | ||
| + | |||
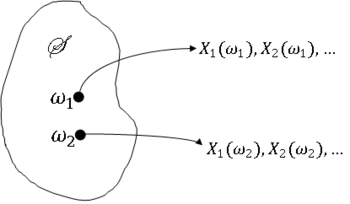
| + | The sequence X<math>_n</math> maps ''S'' to the set of all sequences of real numbers, so for a fixed ''S'', X<math>_1(\omega)</math>,X<math>_2(\omega)</math>,... is a sequence of real numbers. | ||
| + | |||
| + | <center>[[Image:fig1_stochastic_convergence.png|350px|thumb|left|Fig 1: The mapping from the sample space to the reals under X<math>_j</math>.]]</center> | ||
| + | |||
| + | |||
| + | Before looking at convergence, recall the meaning of convergence or a sequence of real numbers. | ||
| + | |||
| + | '''Definition''' <math>\qquad</math> A sequence of real numbers x<math>_1</math>,x<math>_2</math>,... converges to a number x ∈ '''R''' if ∀<math>\epsilon</math> > 0, ∃ an n<math>_{\epsilon}</math> ∈ '''N''' such that <br/> | ||
| + | <center><math>|x_n-x|<\epsilon\qquad\forall n\geq n_{\epsilon}</math></center> | ||
| + | |||
| + | If there is such an x ∈ '''R''', we say <br/> | ||
| + | <center><math>\lim_{n\rightarrow\infty}x_n=x</math><br/> | ||
| + | or<br/> | ||
| + | <math>x_n\rightarrow\infty\;\mbox{as}\;n\rightarrow\infty</math></center> | ||
| + | |||
| + | For a random sequence X<math>_n</math>, the issue of convergence is more complicated since X<math>_n</math> is a function of <math>\omega</math> ∈ ''S''. | ||
| + | |||
| + | First look at a motivating example. | ||
| + | |||
| + | '''Example''' <math>\qquad</math> Let X<math>_k</math> = s + W<math>_k</math>, where s ∈ '''R''' and W<math>_k</math> is a random sequence with E[W<math>_k</math>] = 0 ∀k = 1,2,.... W<math>_k</math> can be viewed as a noise sequence if we want to know the value of s. | ||
| + | |||
| + | Let <br/> | ||
| + | <center><math>Y_n=\frac{1}{n}\sum_{k=1}^nX_k</math></center> | ||
| + | |||
| + | Then, E[Y<math>_n</math>] = s ∀n. But Y<math>_n</math> is a random variable, so we cannot expect Y<math>_n</math> = s ∀n. However, we intuitively expect Y<math>_n</math> to be a better estimate of s as n increases. Does Y<math>_n</math> → s as n → ∞ ? If so, in what sense? | ||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | ==Types of Convergence== | ||
| + | |||
| + | Since X<math>_n(\omega)</math> is generally a different sequence for very <math>\omega</math> ∈ ''S'', what does it mean for X<math>_n</math> to converge? We will discuss different ways in which X<math>_n</math> can converge. | ||
Revision as of 17:11, 21 November 2013
Random Variables and Signals
Topic 18: Stochastic Convergence
Stochastic Convergence
We will now consider infinite sequences of random variables. We will discuss what it means for such a sequence to converge. This will lead to some very important results: the laws of large numbers and the Central Limit Theorem.
Consider a sequence X$ _1 $,X$ _2 $,..., where each X$ _i $ is a random variable on (S,F,P). We will call this a random sequence (or a discrete-time random process).
Notation $ \qquad $ X$ _n $ may refer to either the sequence itself or to the nth element in the sequence. We may also use {X$ _n $} to denote the sequence, or X$ _n $, n ≥ 1.
The sequence X$ _n $ maps S to the set of all sequences of real numbers, so for a fixed S, X$ _1(\omega) $,X$ _2(\omega) $,... is a sequence of real numbers.
Before looking at convergence, recall the meaning of convergence or a sequence of real numbers.
Definition $ \qquad $ A sequence of real numbers x$ _1 $,x$ _2 $,... converges to a number x ∈ R if ∀$ \epsilon $ > 0, ∃ an n$ _{\epsilon} $ ∈ N such that
If there is such an x ∈ R, we say
or
For a random sequence X$ _n $, the issue of convergence is more complicated since X$ _n $ is a function of $ \omega $ ∈ S.
First look at a motivating example.
Example $ \qquad $ Let X$ _k $ = s + W$ _k $, where s ∈ R and W$ _k $ is a random sequence with E[W$ _k $] = 0 ∀k = 1,2,.... W$ _k $ can be viewed as a noise sequence if we want to know the value of s.
Let
Then, E[Y$ _n $] = s ∀n. But Y$ _n $ is a random variable, so we cannot expect Y$ _n $ = s ∀n. However, we intuitively expect Y$ _n $ to be a better estimate of s as n increases. Does Y$ _n $ → s as n → ∞ ? If so, in what sense?
Types of Convergence
Since X$ _n(\omega) $ is generally a different sequence for very $ \omega $ ∈ S, what does it mean for X$ _n $ to converge? We will discuss different ways in which X$ _n $ can converge.